 In Part I of this review, I talked through some of the logistical and ideological challenges facing society in trying to solve the climate and energy supply crises. All pretty grim. But with Part II of my review of the book Prescription for the Planet, by Tom Blees, we’re already through the nadir of depression and apparent helplessness, and on to the optimistic upslope.
In Part I of this review, I talked through some of the logistical and ideological challenges facing society in trying to solve the climate and energy supply crises. All pretty grim. But with Part II of my review of the book Prescription for the Planet, by Tom Blees, we’re already through the nadir of depression and apparent helplessness, and on to the optimistic upslope.
The experimental sodium-cooled EBR-II nuclear reactor, which operated at Idaho National Laboratory for three decades (1964 to 1994).
This post, part II of VI, is concerned with chapters 4 and 5:
– Chapter 4: Newclear Power (pg 117-139)
– Chapter 5: The Fifth Element (pg 141-154)
The play-on-words title of chapter 4 pretty much sums it up. It’s a hand-holding walkthrough of the Integral Fast Reactor (IFR) nuclear power technology that I’ve already discussed on BraveNewClimate in two earlier posts. Blees reckons this is the new, clear choice for future power generation. First there’s some history — a description of the highly successful Argonne National Research Laboratory EBR-II reactor programme which spawned the IFR project (see diagram). Then there’s an excellent primer on basic nuclear physics for the uninitiated, which does a great job at describing how fission reactors work and the difference between thermal light water reactors (almost all present-day nuclear reactors are of this type) and fast-spectrum reactors (like IFR — though Blees tends to use the term fast breeder reactors, I tend to prefer the IPCC AR4 Working Group III terminology, because if avoids those negative historical connotations many people associate with plutonium breeders for weapons).
Importantly I think, considerable space is devoted to explaining the difference between the proliferation-resistant elecrochemical pyrometallurgical processing and recycling, compared to the proliferation-promoting PUREX (Plutonium and Uranium Recovery by EXtraction). This is a key point, because from my wider reading, I’ve concluded that weapons proliferation risk remains one of the greatest hurdle to overcome in convincing most ‘anties’ (Blees’ shorthand for anti-nuclear types) that a large-scale uptake of IFR will not heighten the risk of a catastrophic nuclear exchange or a terrorist attack using nukes.
P131 has a schematic diagram of a ‘pool design’ for a Liquid Metal cooled Fast Breeder reactor (LMFBR), like that deployed in the EBR-II. It’s stunning in its elegance and relative simplicity (the sodium-cooled reactor diagram below, from INL, is similar to the one presented in the book). The design is also ‘passively safe’, in that the inherent physical characteristics of the metal fuel pins means that should they overheat (due, for instance, to a loss of coolant flow or heat sink), they expand, and in doing so decrease their density to the point where the fission reaction simply shuts itself down. No critical dependence on getting those boron/cadmium control rods down in time!
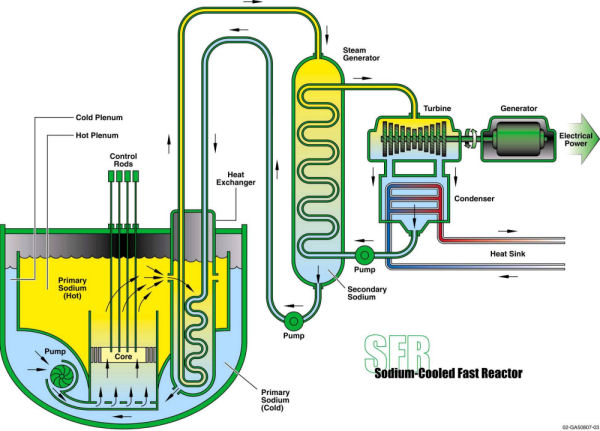 Incidentally, other Gen III+ advanced reactors designs also use ‘walk away’ safety measures, such as having valves holding back emergency cooling water that are held shut by the power system (so if the power goes off for any reason , the valves automatically open and shut down the reaction). But the neat thing with IFR is that it’s the fuel that does the job — although a variety of other safety features are also inherent in the IFR design. Conclusion? The chance of one of these reactor cores melting down, TMI-style, is virtually zero (something like one in a couple of hundred million per year). I could go on here, but really, it’s better to leave it to Blees — go read Chapter 4 if you want to know more about IFR!
Incidentally, other Gen III+ advanced reactors designs also use ‘walk away’ safety measures, such as having valves holding back emergency cooling water that are held shut by the power system (so if the power goes off for any reason , the valves automatically open and shut down the reaction). But the neat thing with IFR is that it’s the fuel that does the job — although a variety of other safety features are also inherent in the IFR design. Conclusion? The chance of one of these reactor cores melting down, TMI-style, is virtually zero (something like one in a couple of hundred million per year). I could go on here, but really, it’s better to leave it to Blees — go read Chapter 4 if you want to know more about IFR!
Now if you thought the chapter 4 material was ambitious, then chapter 5 is no let down either. In brief, it’s a proposal by Blees to replace our liquid fuel dependence — mostly related to our vehicle fleet of cars, buses, trucks etc. — with an alternative, completely recyclable energy carrier. And no, it’s not hydrogen. It’s a pure form of the semi-metal, boron — element number 5 on the periodic table (now you know where the chapter title comes from). We’re into more speculative territory here, because most of the ideas upon which Blees bases his transport fuel vision is theoretical, but it has a solid physical grounding.
For instance, it has certainly been shown that metals can ‘burn’, and that they store an incredible amount of energy per unit volume. Boron, for instance, weight for weight, stores around 20% more energy than petrol (gasoline for the Yanks). It’s just that the fuel tank gets heavier, not lighter, as you burn it, because the combustion products accumulate as an oxide rather than being released as an exhaust gas — so it about equalises with petrol in terms of overall efficiency. To get boron to burn, you need to ignite it in pure oxygen — an idea attributed to a regular commenter at BNC, Graham Cowan — perhaps he can add some further details in the comments section. To reverse the oxidisation, you need to supply energy. Electrical energy will do — derived, for instance from… yep, that’s right, IFR power stations. It’s hard to to this chapter justice in a brief overview — you need to read it yourself to appreciate the thought Blees has put into this nascent yet ultimately very attractive idea. But for another perspective, here’s Jim Hansen’s take on it from his Trip Report (if you recall, I cited his description of IFR prospects in an earlier posting).
 Boron-Powered Cars and Greenwash (Jim Hansen’s notes)
Boron-Powered Cars and Greenwash (Jim Hansen’s notes)
Blees properly ridicules FutureGen, commonly dubbed NeverGen, as a greenwash construction of the coal industry, intended to make it look like they were working on cleaning up their horrendous environmental damage.
Blees suggests that hydrogen-powered cars are a greenwash of the oil and auto industries, while they continue to stick us with gas-guzzlers. That charge may be too strong, but it seems fair to say that they have not been looking at alternative vehicles as hard as they should have been. Also I need to point out a possible personal bias: I have been driving a hydrogen-powered car over the past two weeks [a BMW executive recognized me on an airplane and offered a free trial – for the first time I can look my Mercedes-driving lawyer friends on the level, even though it was just a trial – don’t get excited, the hydrogen cars are not for sale, would be very expensive if they were, and there was only one place, in Jersey City boondocks, where I could fill it up].
Blees thinks that there is a superior alternative to hydrogen. Here is the basis of the idea. If a metal is ground into fine enough dust, nanoparticles, it will burn. We could burn iron-dust in our cars, capture the rust-dust, take the rust home, and cook it to drive the oxygen off, thus recovering our initial iron dust, which we then could use to power our car on its next trip. We supply energy at the time of cooking. Iron is just the energy carrier.
So iron dust is an alternative to hydrogen as an energy carrier to power our post-fossil-fuel cars. Iron dust (unlike hydrogen) has the advantage of being non-explosive, but (among other things) it is heavy and gets heavier as rust. Enter a better idea: boron. It is much more energy dense than iron: it takes a quart of boron to match the energy in a gallon of gasoline. A tank (box) of boron would cost a few hundred dollars, but you only need to buy one tankful, when you buy your car. After that you just take the boron oxide to a store, a Seven-Eleven would be happy to serve, and trade it in for a box of boron (anyone can handle this material). Blees figures that processing boron oxide back to boron would cost only tens of cents. Even if he is too optimistic (or if Exxon/Mobil sees to it that he is put 6-foot under – they are not likely to appreciate competition from Seven-Eleven), it should be much cheaper than gasoline. If the processing from B2O3 back to B is done with carbon-free electricity, it takes care of the carbon emissions problem. Blees, as you might guess, envisages the energy coming from IFR nuclear plants.
O.K., let’s go back a step. It is widely agreed that electric cars can be a solution for a piece of vehicular needs, and plug-in hybrid-electrics are a partial solution for the remaining piece. We should start with those technologies because they are ready to go, and batteries will improve, even though it has been slow going. But we must have something other than gasoline for complementing the electric part. Hydrogen, used in a fuel cell as opposed to being burned in an internal combustion engine, has the great advantage of emitting only water vapor as an exhaust product. Hydrogen could be produced at remote sites where renewable energy, such as wind or solar, is plentiful (or by IFR). But it has technological challenges, as described well in Science a few years ago, and more so in Joe Romm’s book, The Hype About Hydrogen.
Automakers have been working hard on hydrogen for several years. Some of the technological problems must have been solved. All I can say is that the hydrogen-BMW drove great, better than any car I have ever owned, with enough getty-up for even a Texas cowboy (I am not a Texas cowboy). The car also had a gasoline tank, to avoid stranding with no hydrogen, and at push of a button switched seamlessly between hydrogen and gas.
In dismissing hydrogen Blees relies in part on a note by Tromp et al. (Science, 2003) suggesting that hydrogen leakage might threaten the stratospheric ozone layer. But Michael Prather (Science 302, 581, 2003) looked harder and found that it is unlikely to be a problem with realistic hydrogen leakage rates. There are greater challenges for hydrogen, though.
Getting the price of hydrogen vehicles down to a reasonable level is a big challenge and there would need to be a distribution system analogous to gas stations, perhaps replacing them. Boron must have challenges too, but maybe less. Blees says the boron must burn in pure oxygen, which requires miniaturization of an oxygen supply system for the car. I wonder if collecting the boron oxide and converting it back to pure boron is as simple as claimed? Also, the product of hydrogen (in a fuel cell) is water vapor, which we do not have to worry about. That is the big draw of hydrogen: zero pollution. I wonder if we can burn boron without tailpipe pollution?
Bottom line: Blees has stimulating, revolutionary vision. The jury is still out on hydrogen vs boron vs something else. But I am confident that there are better alternatives than fossil fuels. It is time to start working much harder on such alternatives.
———————————————————————————
Part III will look at chapters 6 and 7, covering everything from nuclear batteries to gasified garbage!





.png)
















You can find more information about the Idaho National Laboratory’s Generation IV Systems at http://www.inl.gov/gen4.
[Ed: Now added a link via the excellent picture of a sodium cooled reactor – thanks!]
Yes, Blees and I have been talking about boron since 2000. The publicity Brook quotes from, I think, ORNL is garbled; boron is only about 1.2 times as energetic, weight for weight, as gasoline or diesel fuel, not six times.
The greatest weight the fuel reservoir system of a boron-burning car would reach would be when it was spent, and at this time it would be three or four times heavier than the equivalent gasoline or diesel fuel load in the tank of a car that had just filled up with one of those.
In 1999 I thought this meant boron cars should promptly eject big pieces of B2O3 marked with codes indicating who they belonged to, so that when someone or other collected them and brought them to a power station, the owner could be credited, but it was soon pointed out to me — thanks, Jed — that this was silly. Batteries, even counting their higher chemical-potential-to-wheel efficiency, are 50 or more times heavier than gasoline, so 3-4 times heavier, with advantages, will be world-changing.
Chernobyl was a reactor explosion, not merely a meltdown. The chance of such an event in any Teller-compliant reactor is, as it has been since 1950, identically zero. (Parked cars are much heavier than parked bicycles or motorbikes, but their toppling-over risk is similarly not more, not the same, and not reduced by some factor; it is zero.)
I have recently said more about boron in a paper. I am afraid I may not have attained great readability. If that turns out to be true, skip to the good part at the end. Not right at the end. A little up from there: “5.1 Implications”.
— G.R.L. Cowan (How fire can be domesticated)
[Ed: Thanks Graham, energetic figure updated accordingly]
Tell me more about the oxidation process – how could this happen? Pure oxygen requires storage, compression, energy etc. as well – seems like we’d have to fill up on that as well?
wilful #3: Blees proposes two possible options — a portable oxygen generator (technical challenge is getting one compact/light enough – but apparently surmountable), or, as you suggest, an oxygen tank.
Ignoring the fact that IFR still produces waste that needs to be disposed of, I still can’t see how this is going to be much of a solution.
Wikipedia says that Uranium supplies will last for “more than a hundred years” (but on the same page it says “85″, so I’ll stick with 100). It also says that nuclear power supplies about 6.5% of world energy. Renewables and Hydro seem supply about 7%, so there’s 93% that needs to be covered. That means that uranium supplies will last 100*(0.93/.065) = ~7 years of supply. Of course, that doesn’t take into account projected increases in renewables supply, but it also doesn’t take into account trying to run the world’s transport fleet on electricity…
naught101 #5:
The IPCC have done the numbers on uranium supply (based on OECD figures) – see chapter 4 reference I give in the text above. Working Group III, Chapter 4, pg 271, see Fig 4.10. Using Light Water Reactor technology (one cycle), which uses about 1% of the energy in uranium, there are supplies for 85 years of power at 2004 level of useage, based on identified resources. Adding provable resources increases this to 270 years. Adding unconventional resources such as those contained in phosphate minerals, which are recoverable for 60 – 100 US$/kg, takes it to 670 years. So that is already 47 years at full global supply, based on your maths.
But you’ve ignored the fact that we are not talking about thermal LWR, we are talking about fast spectrum breeders. IPCC estimates identified resources are sufficient for 20,000 years at 2004 levels, and all resources take this to 160,000 years. But just using the 20,000 years and your calculation for full supply, that’s 1,400 years of energy (by which time I suspect we’ll no longer need fission power). The 180,000 years figure takes it to 12,500 years of energy supply – for the whole world.
Regarding waste — the net benefit of IFR expansion is to eliminate long-lived waste, so that it is a highly effective means of reducing waste storage issues rather than inflating them (since it will burn all of the LWR ‘waste’ [read: fissionable material] we currently have lying around). With the IFR fission products below background levels within 500 years, that’s a far cry from the 10,000 to 100,000 time-frames of Pu-239. The waste volume from IFRs is also very small.
Of the 7% or so that renewables currently supply, almost all of it is from hydro, which is unlikely to expand much further (and may decline under climate change).
Do read the earlier thread and follow the links, and read the documents there (and even the ones they link to). It’s a very different technology. Don’t spend more than a bit of time thinking about what would have happened if we’d taken that route 40 years ago. But do understand — this is not Walt Disney’s friend the atom. It’s smarter.
Just to give credit where credit is due: The boron fuel idea is Graham’s from the get-go. As he says, he and I have been talking about it since about 2000, but that talking has been of a nature of mentor to writer. Perhaps a few of the concepts I’ve come up with are slightly different than what Graham originated, and I did dig into oxygen extraction technologies and such with others, but only because Graham led the way. His is an inspired vision that I’m happy to say is being taken very seriously by an ever-widening group of scientists. As far as the paradigm-changing package presented in my book, Graham’s boron fuel concept is an integral part.
In current quantities, liquid oxygen is less expensive (slightly) than bottled water.
From the paper, emphasis added,
Last July 22 I noted at http://www.oxlifeinc.com/freedom5.php a claim that the oxygen denier advertised there would give 300 litres per hour of3 purified oxygen while consuming 0.25 kW. That’s 0.40 kilograms per hour if the temperature is 20°C and the pressure is 1 atm. Weight of the unit, approximately 14.5 kg.
How much power can a boron-oxygen heat engine, with a typical 30-percent heat engine efficiency, make using 0.40 kg/h of oxygen? 1.85 kW. 1.6 kW would be net. A car with 200 kg of the units — 14 of them — would net 22 kW, 30 hp, with which to cruise all day.
Or anyway, that is how it was six months ago. Medical technology developers have been driving rapid reduction in these things’ size and power consumption. Blees performs an invaluable service by writing enthusiastically, but he tends to take American national laboratory authorities too seriously. They’re likely enough to explain to you at length that an oxygen-concentrating boron motor must put at least a third of its output back into oxygen concentration, interrupting themselves only to take a hit of medical oxygen from a device that, as above said, would take less than 14 percent.
Still, without ORNL, the world might never have had that visualization of the word “BORON” swooping spectrally into a gas tank. At http://www.eagle.ca/~gcowan/BonCu2.jpg you can see some actual boron.
Correction, 0.4 kg/h oxygen at 30 percent makes 0.82 kWh, so the net is 0.57 kW, and the oxygen denier’s take really is almost a third.
The problem with a boron powered car is that it is still a thermal engine, which means that the efficiency is inherently low, and why fuel cells are at least conceptually more attractive.
Does a boron engine require pure oxygen, or can it run on oxygen-enriched air with some remaining nitrogen? (Is the problem the same as with gasoline, production of nitrogen oxides, or does nitrogen in the gas interfere with the boron engine?)
Is there any oxygen concentrator now available that produces pure oxygen? Or pure enough for a boron engine to run on?
The medical references I find comparing concentrators to oxygen tanks comment that the oxygen level the patient is breathing is lower when supplementing from the concentrator than from the tank. But I didn’t find numbers.
I found mention of aircraft devices that can produce pure oxygen, e.g.
US Patent 5,071,453, 1991 – freepatentsonline.com
… oxygen output … in either, dilution mode (less than 100
percent concentrator output) or the 100 percent mode (pure oxygen)
This long-term payer of attention has, he says, distinct memories of scores of conceptually attractive vehicles sitting on dealer lots month after month, unleased.
Also note that if fuel cells were long established as cars’ main fuel energy converters at mid-30s gross efficiency — has any vehicle fuel cell done better? — and heat engines were the putatively keen putatively new thing, their fans could point to their conceptual efficiency. Automotive heat engines operate between the temperature of a fuel-air flame, mid-2000s K, and that of a heat exchanger suitable for lightweight dumping of kilowatts, maybe 320 K, so the cars being driven off lots today are conceptually getting heat-to-work efficiency percentages high in the 80s.
Yes, see the paper‘s “Oxygen denier readiness” section.
> the cars being driven off lots today are conceptually
> getting heat-to-work efficiency percentages high in the 80s.
Is this astonishingly high?
It’s the complement of T-low upon T-high.
[…] Prescription for the Planet – Part II – Newclear energy and boron-powered vehicles […]
[…] Prescription for the Planet – Part II – Newclear energy and boron-powered vehicles […]
[…] Prescription for the Planet – Part II – Newclear energy and boron-powered vehicles […]
Re the Fuel Conditioning Facility located next to the EBR-II, is that being looked at by the industry folks? It sounds like those could be built _before_ the GenIV plants, if they can process fuel from earlier designs. Or is it chicken-and-egg, is it feasible to operate this form of reprocessing if you don’t already have a GenIV plant right next to it?
(Could the reprocessing plant be built within a space sufficient to later add the GenIV plant — which would basically mean building the reprocessing plants next to the older coal power plants, I guess? — well, they’d need the railroad connections for that.)
http://www.gnep.gov/pdfs/Goff_Electrochemicalposting.pdf
Electrochemical Processing of Spent Nuclear Fuel
Dr. Michael Goff, Idaho National Laboratory
Nuclear Regulatory Commission Seminar
Rockville, MD March 25, 2008
____excerpt_____
Electrochemical Processing
Until 1994, focus was on demonstration of closed fuel cycle
with a fast reactor.
– Recycle of fast reactor fuel
– Limited work on production of fast reactor feed material from LWRs
In 1994, activities were redirected to treatment for disposal.
– Engineering-scale experience was gained with spent fuel.
With the formation of the Advanced Fuel Cycle Initiative (AFCI) in 2002 and the Global Nuclear Energy Partnership (GNEP) in 2006, recycle focus was renewed and stressed.
_________________
[…] has for energy storage and transport in our energy future, compared to alternatives such as metal-combustion (my bet is that the latter will prove to be a superior technology, e.g., due to its avoidance of […]
[…] up’ on Integral Fast Reactor nuclear power is in written form of one sort of another: books, popular science articles, blog posts, and so on. But there’s plenty more out there. One fun […]
Boron cars are a nice Idea but if you have abundant nuclear energy there are several easier paths.
A. CO2 + H2 = Methane CH4 and water (nickel Graphite catalyst in the garage or a clean combustion power plant) CH4 and another catalyst makes ethane and a third catalyst makes octane: That´s petrol. {clean coal technology should be designated clean combustion; it will work on biofuels drawing down on atmospheric CO2}
B. Make biogas from sewerage, lawn clippings etc. Use the abundant energy from your nuke to strip out the CO2 in biogas; Its 50% CO2 50% CH4. Compress into an LNG tank in a car with a little more length to its wheel base so you get your gas tank and keep your big boot. Dry the biogas sludge to make fertilizer.
C. If you have abundant energy make Aluminium pellets. Under the bonnet feed them into sodium hydroxide and water. Foom You have hydrogen in the carburettor or injector. A KG of Al will get you many miles in an efficient car. The hopper of Aluminium oxide is traded for an empty hopper [and a bag of pellets] at a recharging station. There Your abundant energy is used to power the production of more pellets.
There are several more like that. Nuclear is not even required. All of these recycling technologies; boron, aluminium, carbon work on a time independent basis. They can use solar and wind power when its available and pause the factory when these power sources are unavailable.
[…] have already reviewed Chapters 4 and 5 of P4TP, here. The downloadable chapter covers the following […]
[…] or using stationary energy inputs to create chemical-electric batteries, hydrogen fuel cells, purified metals, etc. In the former case, the enegy input comes from a solar source in the form of biomass (via […]
Probably taking a trip back to Sir Isaac Newton days here but…. How about mechanical energy plus electricity for vehicles? There could be lots of springs in a car that release power gradually and keep an alternator of some sort going to keep the batteries charged. The batteries would actually run the vehicle by powering a computer system. It would take a complex system of high-tension springs to be efficient. Just scale up a spring-powered toy car with some major modifications. It would have a computer system governing the vehicle’s acceleration or deceleration. This would eliminate the need for a transmission of more than three gears; just forward, reverse and wind-up mode. You could have wind-up stations, and have a gear switch for wind-up mode of the back tires. Completely take combustion out of the equation; it seems unnecessary for ground transportation; bicycles go up to 50 mph…downhill…probably. I’m no physicist, computer or mechanical engineer, but I’m working my way toward becoming one of the three, so just dismiss this if it’s completely stupid. Thanks!
Range scales as the zeroth power of size, i.e., doesn’t change. Insects that specialize in jumping, and people that so specialize, show the same phenomenon, because both have the same limitations on energy stored in fast-acting muscle: both fleas and basketball players can, by jumping straight up, raise their centres of mass about one metre.
Interestingly, they do this with muscle that is only a small fraction of their total mass, but a coiled spring, which is 100 percent strained metal, can’t jump any higher. You can probably easily confirm this if you have a retractable ball-point pen: they usually contain a small spring.
And presumably the batteries feed an electric drive motor. These intermediary stages consume energy. If a directly spring-driven Prius would go 25 metres, one with the electric stuff between the springs and the wheels would go 15 to 20 metres.
(How fire can be domesticated)