Guest Post by Peter Lang. Peter is a retired geologist and engineer with 40 years experience on a wide range of energy projects throughout the world, including managing energy R&D and providing policy advice for government and opposition. His experience includes: coal, oil, gas, hydro, geothermal, nuclear power plants, nuclear waste disposal, and a wide range of energy end use management projects.
[Ed: Peter is seeking feedback. Some reviewers comments he has already received are given at the end of this document, for reference.]
Pumped-Hydro Energy Storage – Tantangara-Blowering Cost Estimate
Introduction
Energy storage is essential for intermittent renewable energy generation and is valuable with coal and nuclear generation too. Pumped-hydro is a mature technology and is generally the least cost option for large scale energy storage.
This paper provides a rough cost estimate for a pumped-hydro energy storage facility that would utilise existing dams and reservoirs in the Australian Snowy Mountains Hydro Electric Scheme.
The paper is in response to questions about the cost of pumped hydro energy storage, especially as a component of a fossil-fuel-free electricity generation scenario for Australia. The paper is the fourth in a series of articles (see here for a listing — search this page for articles authored by Peter Lang).
Project Description
The proposal is to build a 9 GW pumped-hydro facility by connecting two existing reservoirs with tunnels, pipes, generators and pumps.
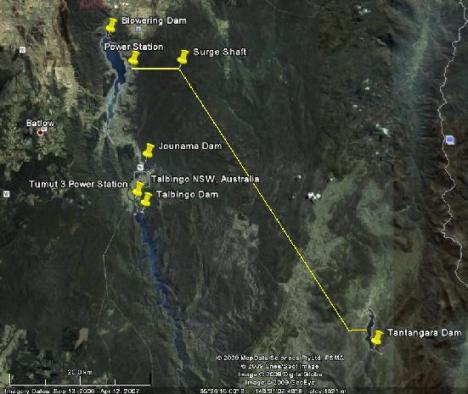
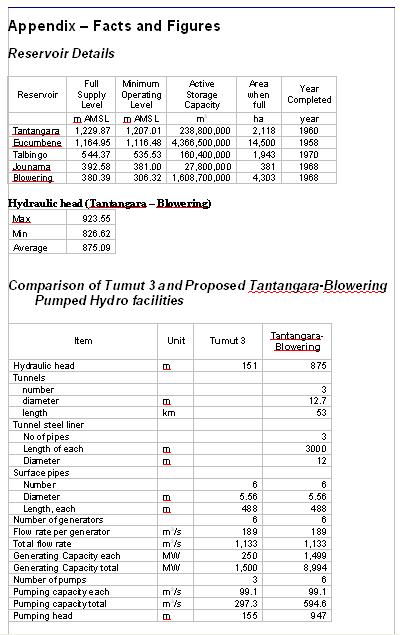
The two reservoirs are Tantangara (the upper reservoir) and Blowering (the lower reservoir). The difference in elevation between the water levels in the upper and lower reservoirs is 875m (see Appendix). The tunnels to join the two reservoirs would be 53km long (Figure 2).
The facility would generate 9GW peak power, for 3 hours per day from 6 hours of pumping at full pumping rate. It could generate for longer at less than 9GW, or if pumping was for longer than 6 hours per day, or if the pumping rate is greater than assumed in this analysis.
The proposal is to bore three tunnels, each of 12.7m diameter, to link the two reservoirs. The reservoirs would be tapped near their down-stream ends to maximise the volume of water storage available. About 3km of the tunnel at the lower end would be steel lined to prevent leakage. There is just about sufficient ground cover along most of the remainder of the tunnel route to avoid the need for waterproof lining or grouting for most of the remaining 50 km of tunnel.
The rocks to be tunnelled through would be mostly granite and similar strong, hard igneous rocks. There may be some hard sedimentary rocks, possibly including minor amounts of limestone. The rock would be fractured and faulted.
The power station is assumed to be similar to Tumut 3 in that it would have six turbines in a power station of similar size to Tumut 3. The differences are that the power output will be six times that of Tumut 3 (because six time the hydraulic head). There would be six pumps rather than the three at Tumut 3. Another difference is that some 3km of steel lining will be required in the tunnels.
 Issue – Francis turbines, which are best for pump storage, currently have a hydraulic head limit of about 600m. Tantangara-Blowering is 875m hydraulic head. The manufacturers are working on increasing the upper limit. I understand manyufacturers are working at the moment to double them up.
Issue – Francis turbines, which are best for pump storage, currently have a hydraulic head limit of about 600m. Tantangara-Blowering is 875m hydraulic head. The manufacturers are working on increasing the upper limit. I understand manyufacturers are working at the moment to double them up.
Cost Estimate
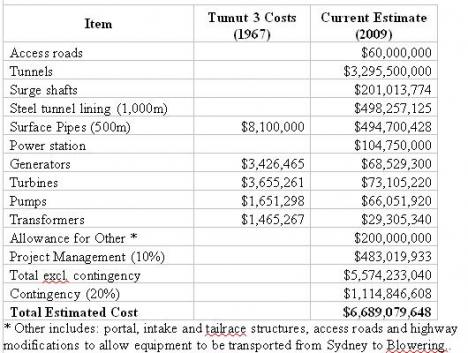
The table below provides a ball park cost estimate for the scheme. The tunnel costs, the main component, were calculated using costs for rock tunnel excavation from world wide experience. The power station, pumps, etc, were estimated by multiplying the original costs (from 1967) for Tumut 3 by 10 (that is approximately how much inflation between 1967 and 2009), and by doubling the cost of this equipment to allow for the six times greater water pressure and, therefore, power output. The greatest uncertainty is the cost of the steel pipes, tunnel lining, power station and ‘Allowance for Other’.
How realistic is this cost estimate?
World experience is that hydro projects cost about US$2,000/kW to US$4,000/kW. The Electricity Storage Association gives a range of costs for Pumped-Hydro of US$500/kW to US$1500/kW. This project is A$744/kW.
So the proposed Tantangara-Blowering facility is towards the low end of the range (if the figures are correct). The main reason for the lower than average cost is that the reservoirs do not have to be built; they already exist. However, this project requires more tunnelling than is normal for pumped-hydro facilities.
Conclusions
The Tantangara-Blowering pumped hydro scheme would be a high capital cost investment for just 3 hours of peak power generation per day.
This is the most economic of the four projects investigated.
Pumped hydro is often economically viable for providing peak power for a system comprising mostly fossil fuel and/or nuclear generation (France’s system is the ideal example). But pumped hydro is not well suited to intermittent, unscheduled generators.
I would like to acknowledge the help of some friends, all of whom have had a life time of experience working on hydro-electric projects around the world (all but two still are). Our work on hydro sites and our friendship go back 39, 33, 33, 29, and 19 years. I would like to thank Rich Humphries and Dr Derek Martin for their invaluable assistance (and for taking time off from catching neutrinos to help me: they are building a large underground cavern deep below Sudbury, Ontario to catch neutrinos that will be beamed through the rock from Chicago); Tim Little (Canada), Andreas Neumaier (currently in Asia) both of whom have a life-time of experience designing and constructing hydro-electric projects; and David Purcell who was the first boss I had who could influence me. He grew up in Cabramurra, the construction camp for the Tumut 1 and Tumut 2 projects in the Snowy Mountains Scheme. On weekends he would go with his father, a civil engineer, around the scaffolding and walk-ways as he checked out the construction work and instrumentation on the Tumut Pond concrete arch dam, Tumut 2 Dam and the Tumut 1 and Tumut 2 underground power stations. What a way to start a life. Certainly, today’s young can’t get that sort of early experience of the real world.
Pumped hydro is an excellent match for nuclear and for dirty brown coal fired power stations (because they run at full power all the time and produce very cheap power). Consider the 2007 NEM demand: Peak = 33GW, average = 25GW, base-load = 18GW. Option 1 – nuclear only. 33 GW @ $4b/GW = $132b. Option 2 – nuclear + pumped hydro. 25 GW nuclear @ $4b/GW = $100b + 8GW pumped hydro for $15b = $115b. Conclusion: Option 2 (nuclear + pumped hydro) is the lower cost option.
Reviewers’ Comments
Reviewer 1
I had a quick look at your idea of a pumped storage scheme between the Tantangara and Blowering resevoirs in the Snowys. I have only spent a couple of hours looking at your numbers for the assessment of the technical and economic viability of such a scheme. It is my personal view as an individual and not that of the company I am working for.
Ok, here comes the technical side:
1. One would have to assume that the available head is between the minimum operating level at Tangagara, MOL = 1,207 and the full supply level at Blowering, FSL = 380 because any operator would have to guarantee 95% reliability for his peaking power. Thus, the gross head for power generation is MOL – FSL = 827 m
2. Assuming 3 No.s tunnels of diameter D = 12.7 m gives a cross sectional area of Atot = 380 m2.
3. Assuming a maximum flow velocity of v = 3 m/s to keep friction losses within a reasonable range, the total discharge Q = v * Atot = 1,140 m3/s.
4. With that and assuming a local and friction loss factor of η = 0.85, the energy P computes to be P = 7,860 MW using the formula
P = (9.81*η*Q*H)/1000
5. Assuming an operating time of T = 3 hours/day the available energy is E = P * T//1000 = 8.6 GWh/year
6. The discharge volume V = Q * T * 3,600 = 12.3 106 m3.
7. With a reservoir area of Ares = 2,118 ha and assuming vertical reservoir walls, the drawdown over the 3 hour operating period will be Δh = V/Ares = 0.6 m which is acceptable from an environmental and safety point of view, I think.
8. Assuming that the operator can sell peaking power at 4 times the rate as he has to buy the power for pumping during off-peak times, say $0.60 generating vs $0.15 pumping costs, the annual revenue from the scheme would be R = ($0.60 – $0.15) * 8.6 106 = $3.87 billion per year.
9.I am not a mechanical engineer but I believe that at a head of H = 827 m you are pushing the envelope of what turbines can take. I also think that you may need more than 3 units, say 6 or 9 to keep the size of the turbines and pumps and the width of the underground cavern to a reasonable size.
Now comes the project cost sides:
1. The tunnel is by far the most expensive single item so I have focused on that. I do not have a price for a 53 km long, 12, 7 m diameter tunnel excavated by TBM so have used a 8 km long, 3.5 m diameter tunnel and scaled it up to give an approximate figure for the bigger tunnel. Assuming that the tunnel will be mostly unlined and constructed in essentially sound rock, the costs for excavation, support and care of water during construction is $ 7.56 109, which more than double your figure.
2. You have scaled up the 1967 costs of T3 to arrive at the other major cost items. If my tunnel cost figure is correct, I fear that the other cost items may also be higher than what you have estimated.
3. If this is the case, the construction costs may be closer to $15 billion than $7 billion as you have estimated, which will bring the cost per installed kW back into the range of $2,000/kW which is about what pumped storage schemes cost these days.
I do not mean to discourage you but the capital expenditure for a pumped storage scheme between Tantangara and Blowering seems prohibitive because of the scale of the investment, the high up-front costs and the long period for investors to recover their money. Unfortunately, politicians and banks take a much shorter view of life when it comes to political or financial gains and it seems to me that your idea, as much as I like hydro, seems to be condemned to the ‘not economical’ basket.
Reviewer 2
I took a quick look at your costs and determined that it would take more time than I have to review those adequately. We have had a lot of challenges with cost escalation over the last several years (until the last year or so) and I would not want to give you a misleading opinion. That said, I do have some quick comments on your proposal:
– The proposed capacity of 9GW (9000 MW) is huge. Compare to Itaipu (12,600 MW), previously the world’s largest hydro plant and now Three Gorges (ultimately about 22,000 MW) or Revelstoke (2000 MW, soon to be 2500 MW when Unit 5 is completed).
– The proposed number of turbines is 6, which translates to 1500 MW each. I believe the world’s largest turbine capacity to date is about 750MW. (e.g. the turbines at the Sayano-Shushenskaya dam in Siberia which recently experienced the world’s worst hydro plant disaster to date – check it out on Google if you are not familiar already).
– The head is very high as you note. I believe Francis turbines have been built for heads as high as about 800m, but probably not for large capacity.
– Your overall cost looks quite low at less than $800/kW; as you note, world experience is typically several times that today.
– Your stated uncertainty of 25% is too optimistic. When we do a conceptual level estimate by a qualified estimator, we state that the uncertainty on the upper end is as high as 100%. The uncertainty goes down as more design is done, and we would not claim 25% uncertainty until we were into final design.
– Steel lining is one of the more critical cost factors. For many high head projects, the cost of steel lining is the factor that determines whether the project is economic or not. You need to know in situ stresses etc to do a proper analysis.
Filed under: Nuclear, Renewables






.png)
















Thanks for this analysis Peter. Very interesting.
Given that even if tyhe impediments to rolling out nuclear power disappeared tomorrow, we would be burning gigatonnes of coal before dispensing with the last coal plant in favour of the latest nuclear plant, even if the total did come to $132 billion for the combination NPP + pumped storage it would probably still make sense.
After all, if one can reduce the CO2 intensity of coal and gas by judicious management of coal and gas plant operation that’s still an advantage. If less redundant capacity for the renewables we are going to have is needed then that too is an advantage.
And of course, our total stationary energy demand by 2030, 2040 and 2050 is bound to increase, especially if significant transport capacity is on grid, so the facility is hardly likely to be wasted.
Peter – Excellent post, thank you.
I wonder if you could explain your conclusion “Pumped hydro is … not well suited to intermittent, unscheduled generators” in a little more depth, as this wasn’t really discussed in the body of the paper. I assume this is because (in this example) it can only generate peak power (9 GW) for 3 hours a day, which is problematic when considering total density and volume of electricity in a grid powered by intermittent sources, but I’d be keen to understand it properly.
Cheers.
115 billion dollars is a very large amount of money. Is spending that much, even over a number of decades, even in the realm of possibility? I ask because this is mostly discussion from an engineering perspective, however that is not something the public is interested in. How much will it cost the average Australian? Apologies if these questions are too much in some way or another.
Thanks.
Teekay
I think its more a question of the fact that the pressure in pipes has to be maintained by a constant and steady supply of power to the pumps over several hours. Intermittent sources by definition can’t meet this standard.
Scott asks:
Well if we are talking 30 years, for example, that’s less than 4 billion per year or less than 0.4% of GDP. By way of reference, the government is negotiating over a submarine contract which is going to cost between 25 and 40 billion dollars. The national broadband network fund is $43 billion (most of it private but the government is backing the project funding).
So the money is there and in the end, the bulk of it is for installed energy production assets that have to be built. Those coal and gas plants have to be replaced sooner of later and in the end, someone will pay.
On the income side on both coasts of the country a number of massive LNG projects have just been announced probably beginning 2015 the revenue from which will dwarf the sums we are talking about here.
Ewen @ 5 April 2010 at 19.11
I am not quite clear what you are asking or stating in this first post. I’ll try to answer, and please ask again if I’ve misunderstood.
You are correct that demand will increase and it will take at least 30 years, probably longer, to replace all the coal fired power stations. This papers shows projections of demand and the replacement of coal generating capacity with other options between 2010 and 2050. http://bravenewclimate.com/2010/01/09/emission-cuts-realities/
Pumped hydro will not reduce the CO2 emissions intensity. It actually increases it because the efficiency of the pumped storage system is about 7%5 to 80%. So we need to burn say 5 tonnes of coal for pumping and then we get the energy equivalent of only 4 tonnes of coal when we generate from the pumped hydro. Gas generators would not be used for pumping because gas is far too expensive; similarly with wind and solar, even if they could provide reliable constant power in the early hours of the morning. Coal and nuclear are ideal for puimp storage because they produce cheap power in the early hours of the morning when demand is low. So there is no demand for the power from hydro and little other demand for the power from the coal fired generators.
The $132 billion figures was for the all nuclear option to replace all the current generators in the NEM. The alternative with 25GW nuclear and 8GW hydro would cost $115 billion. So this option is cheaper. (reserve capacity margin ignored in these figures for simplicity). I doubt pumped hydro is economic in Australia at the moment. Gas can do the job more cheaply and with less emissions than using brown coal (the cheapest) for pumping.
Does this address your points?
TeeKay, on 5 April 2010 at 19.35 Said:
I had intended to rewrite the paper after the reviewers comments and also address your question. But never got around to it. Thisew who were following the discussions with Neil Howes last year, will recognise that this paer stemmed from those discussions.
Hydro is an excellent mix with intermittent renewables because when the intermittent renewables are generating the hydro does not, so it saves its stored energy (the water stays in the storage reservoir for future use. But this is not the case with pumped hydro. With pumped hydro we need constant, reliable power when the demand on the grid is low. That is from about midnight to about 6am (refer to the last chart in the article above and not the time of low demand). So for this reason alone solar and wind power are totally unsuited to pumped hydro.
But there is another reason to. As the Reviewer # 1 above pointed out, the power for pumping needs to be purchased at about ¼ the price the power will be sold. Wind power costs about $110/MWh and solar abour $250/MWh, where as the baseload power from coal in the early hours of the morning is probably around $30/MWh. So wind and solar power (and gas) are too expensive for pump storage. The power from pump storage would be sold at peak power rates. (readers will appreciate I am simplifying everything here).
Scott, on 5 April 2010 at 19.44 Said:
Scott, I think you may not have seen this paper: http://bravenewclimate.com/2010/01/09/emission-cuts-realities/
It is an important background to all these discussions.
The spending of $115 billion would be over the period 2010 to 2040. However, if we didn’t have to spend it on nuclear, we’d have to spend it on replacing the existing coal fired power stations either with coal or with gas. We would need to spend about $2 billion per year for 40 years if we replaced with coal. So the extra cost is about 35 billion for nuclear and gas over a period of 40 years. The paper above shows the projections of capital expenditure, capacity of each technology, CO2 emissions, and electricity cost (for the substitutions) for six technology mix options (coal, gas, nuclear, wind and solar).
As Ewen pointed out, to put tthe $35 billion extra expenditure over 40 years in perspective, we have committed to a federal debt of $200 billion in the past year, spent $3 billion on pink bats insulation and committed to $43 billion for a national broadand network (mostly private sector funding is hoped but that is unlikely to happen).
By the way, I just noticed. Barry has been very cunning. If you click on the photo of the Tumut 3 power station, it takes you to a satellite view of the project and several other photos,
Thanks for your response Peter, that makes sense to me now. I appreciate the simplification too.
As far as I can tell there’s also no way pumped hydro could complement the renewable-only advocate’s notion of “efficiency” as a solution, as the process would have to be an overall net consumer of energy. It just makes good economic sense, in terms of peak revenue, if you have reliable baseload generators.
Good article Peter. For the sake of reference what sort of continuous output could this project deliver with the water inventories it collects from the natural catchments?
Pumped hydro certainly has a place but this idea looks to be in the engineers pipe dream class.
Apart from all the technical and cost problems it is just way too big and centralized which exposes the grid it feeds to reliability issues.
One issue could be water.I was at Tantangara Reservoir last year and it was virtually empty-below the tunnel outlet to Lake Eucumbene in fact.
Australia would do better to concentrate on smaller,dispersed generation,not mega projects.
An alternative approach might be to deliver unregulated electricity from nearby to dedicated pumps at the discharge area. The water is simply sent back uphill to the lake in a short steep pipe, no tunnels or major concrete works needed. The motors would be variable speed and the pumps would be positive displacement such as helical rotor. I have no idea how much it would cost or the round trip losses.
If Tasmania had the export capacity several dams would suit this approach. There are two vacant slots for 150 MW Francis turbines at Gordon Dam, suggesting river flows didn’t meet expectations. The King and Pieman catchments are very close to the windy west coast. Maybe there is 2 GW in it at unknown expense including building a second underwater HVDC cable for export. In reality Tasmania now imports more and more coal fired baseload electricity from the mainland since the existing cable was built. For the zinc, steel and aluminium electrorefiners it is a case of ‘out of sight out of mind’.
I misled readers in my post at 5 April 2010, 22:03.
The $35 billion extra is the additional cost to build 25 GW of nuclear and 8 GW of pumped hydro instead of replacing the retiring coal power stations with new coal. However, this does not take into account the demad growth. 25 GW was the average demand for 2007 and 33 GW the peak demand in 2007. The demand will increase over the 30 to 40 year replacement period, so obviously more cpacity will be required and this will cost more than the $35 billion I mentioned in my previous post. Based on the assumptions in the paper here http://bravenewclimate.com/2010/01/09/emission-cuts-realities/, (such as high cost nuclear), Figure 9 shows that the extra capital expenditure, cumulative to 2040, would be about $80 billion ($180 billion for coal and gas instead of $100 billion for coal). Figure 8 shows the projected capital expenditure per 5 years from 2010 to 2050. Divide the capital expenditure in Figure 8 by five to get the annual capital expendityre. Subtract the capital expenditre for BAU (Business as Usual) from ‘Nuclear & Gas’ to get the additional capital expenditure that is due to building nucear and gas instead of new coal.
DV82XL, on 6 April 2010 at 1.23 Said:
That is a complicated question. Here is some of the answer.
The upper reservoir Tantangara) is the smaller of the two. If it was full, and if there was no restriciton on the rate of drawdown, it could run at full power (9GW) for 58 hours. Great in an emergency where the grid goes down. That was the easy part to answer.
(As an aside, one of the really great things about hydro is it can restart the grid from scratch if there is a total failure).
Now for the harder part. Tantangara’s role is to capture water in the headwaters of the Murrumbidgee River and divert the water to Eucumbene, which is the Snowy Mountains Scheme’s large, central storage reservoir.
Another aside – (I love this stuff) Eucumbene is the key to the Snowy, and a great story in itself how it came to have this role (thanks to Sir William Hudson, a highly regarded consultant from the Tenesseee Valley Authority and a long horse back ride around the scheme in the early 1950s).
Water transferred from Tantangara to Eucumbene falls some 100 m without generating electricity. Then it runs down through three power station (Tumut 1, 2 and 3) to Blowering Reservoir.
This is going to get too complicated to explain here. The short answer is that I have based the scheme on pumped hydro only and no generation from the normal inflows to Tantangara. The economics of the scheme would be improved by using some of the Tantangara catchment water for generation. How much would be an economic decisions and a whole stack of other factors.
Teekay
Dead right. Well summarised. You’ve got that in one. Please explain it to Mark Diesendorf and Mark Jacobson. 🙂
Podargus, on 6 April 2010 at 5.50 Said:
I agree. It is not viable. I wrote this up because greenies kept bleating about how much pumped hydro storage capacity was available in existing dams in the Snowy Mountais Scheme and elsewhere. They keep raving on about how “we can have masses of cheap pumped hydro storage and Compressed Air Energy Storage available in existing dams. They reckon the problem is that no one takes any notice of them. So that is whay I wrote this up. And this is about the most economic scheme available. Anything else would provide more expensive electricity.
I presume you do realise of course that we don’t need to build the full 8 GW. We could build smaller amounts, built incrementally, and we could build similar but more expensive schemes elsewhere.
I presmue you did read right through to the Reviewers’ comments, since they said much the same as your comment.
The reason you saw it empty is because Tantangara’s role is to divert all its water to Eucumbene. It needs to be enpty before the seasonal inflow season starts so it can capture as much of the seasonal inflow as possible. But this is irrelevant to the pumped hydro scheme because the pumped hydro uses only the water pumped up from Blowering. The water level in Tantangara Reservoir would rise and fall by about 0.6 m each day (when the reservoir is full, more when empty).
No that is wrong. Distributed systems are far more expensive. Probably orders of magnitude more expensive.
The so called distributed wind and solar systems are EXTREMELY centralizing and very susceptible to common-mode failure.
Here is the aggregate wind power production of the entire nation of Germany: http://i47.tinypic.com/8xjuw6.jpg
It acts not as tens of thousands of individual turbines; it acts like a single unreliable 25 GW generator.
What is the typical solution offered to this problem by self-professed greens? They range from build a massive pan-european grid and intricately coordinate the various countries rather than the loose coordination of today to building weeks of electrical storage at massive centralized facilities.
What’s the solution taken by Germany in reality? Build a big gas-pipeline to Russia.
The decentralization of “renewables” is a mirage.
Why not connect talbingo->tantangara (which is much closer at ~20km)?
Hi Dashpool,
That is a really good question and it was discussed at length on another earlier thread.
The main reasons why I did the analysis on the basis of Tantangara Blowering (T-B) rather than Tantangara-Talbingo (T-T) are:
1. The greater hydraulic head difference (that is the difference in elevation between the water levels in the top and bottom reservoirs), and therefore more power available from T-B than T-T (see the Reservoir Details in the Appendix).
2. Talbingo is maintained near full to maximise the head for generation in Tumut 3. The operators manage the level in Talbingo by controlling the rate they release water from Eucumbene and down through Tumut 1 and Tumut 2 to Talbingo. They also have to keep enough storage space in the top of Talbingo to hold the water Tumut 3 pumps up at night (Tumut 3, as you probably know, is a pump storage facility itself). So, without knowing much about the operating constraints, I guessed that running another pump storage scheme using Talbingo might compromise the overall efficiency and flexibility of the system.
I actually did a rough comparison of power, storage and cost for four options:
1. Enlarged Tumut 3 including pump back from Blowering
2. Eucumbene – Talbingo
3. Tantangara – Talbingo
4. Tantangara – Blowering
Tantangara Blowering was the most economic based on my very rough calculations. However, as the two reviewers pointed out, I probably underestimated the cost by a factor of 2 or so, so a more expert analysis might find your proposal, Tantangara Talbingo, to be a better proposition. If you are able to do this comparison, it would be great if you could post it here.
Well, I would be interested to see why your Tantangara – Talbingo was relatively expensive.
Basically, the head is ~720m instead of 875m, so not so much different. For same flow rate, 6.5GW instead of 8GW.
The tunnels would be ~20km long instead of 53km long. Assuming the flow rate is limited by losses inside the tunnels, it would be reasonable to use two tunnels instead of three to get the same proportional drop in head due to friction losses. (a quick calculation gives losses of the order of a couple of percent one way)
I can’t figure out what cost methodology you used for the tunnels, but assuming
the cost is proportional to volume excavated, this would reduce the cost of the tunnels by almost a factor of four. As the reviewer points out, your tunneling costs seem low compared to comparable projects (e.g. Gotthard base tunnel per unit volume).
Since almost all the major cost items are proportional to tunnel cost, this would seem to massively reduce the cost of the project. The sides of talbingo and blowering are pretty steep, so 1km seems adequate for lining. $250,000/m should buy quite a lot of steel. Rougly adjusting your figures, the cost would be about 3.5 billion dollars instead of 6.7 billion.
I don’t know what the interoperations with tumut 3 would involve: this might be inside the margin of error for a project of this scale.
Hi dashpool,
I can see from this post that you do know quite a lot about the subject. I’ll give you some quick responses now, but I’ll have to wait until after the weekend to look back at the four cost comparisons.
I agree.
No this is not correct. We’d still need to keep the flow velocity at about 2.5m/s so we still need three tunnels. I agree, therfore, that the cost of the tunnels would be roughly 20/53. The length of the steel lining would be roughly the same if the topography is the same at the down stream end. So we’d still need 3km of steel tunnel liner. This is a mjor cost item. The steel liner design is explained here: http://140.194.76.129/publications/eng-manuals/em1110-2-2901/c-9.pdf
The tunneling costs were determined from Figure 24 here http://www.rocscience.com/hoek/references/H2001b.pdf and escalated to 2010. However, I now understand that this does not include all the costs for such tunnels, hence the comments by both reviewres that I had probably underestimated by about a factor of 2.
No that is not a correct assumption. The power station and equipment will change little. The steel liner, a major cost item will not change in length, but the steel thickness will change by the reduction in hydraulic head. The tunnel will change by about 20/53 roughly and this is applied to roughly half the costs. The surge shafts will not change. Most items don’t change. Very roughly I see the cost of TT/TB = 75% and the power of TT/TB = 70%. This is very rough. Ialso think the constraints on managing the storage in Talbingo are not insignificant. Talbingo was designed to poperate with Tumut 3 and as part of the Eucumbene to Blowering generating and pump storage system. We cannot expect to make a mjor change to the top reservoir of Tumut 3 and not have a significant impact on the total system.
dashpool,
I would consider that Tantangara-Blowering would be in the order of $15 billion and Tantangara-Talbingo in the order of $12 billion.
By the way, I seem to recall (but may be wrong) that Talbingo did not have sufficent storage volume to make full use of the available storage capacity at Tantangara, So in the TT case Talbingo is the constraint, whereas in the TB case Tantangara is the constraint. That is from memory, I might have that wrong.
Dashpool,
I just realised I made a mistake in my quick calculation of the change in power. TT/TB = 82% not 70%. This swings the conclusion towards wht you are arguing. So I’ll have to look back at my original comparison. However, I don’t expect to be able to do so before Monday.
Woops again. I accepted your 720m hydraulic head for TT. It is actually about 670m. So the power ratio TB/TT = 76%. This is roughly what I expect the ratio of the cost to be also. But the TT option has major constraints on storage in Talbingo reservoir. So much so that I expect it would be less economic than TB.
Sorry to go off topic but I thought this was interesting. It suggests that maybe fusion is hotting up as an alternative in the not to distant future.
http://www.abc.net.au/news/stories/2010/04/06/2865472.htm?section=justin
Sorry about my mistake in the head calculation.
The TT proposal would involve a height change of ~0.7m on Talbingo (which has approximately the same area as Tantangara). This is less than a tenth of the working head range of Talbingo. Why do you think this would pose a major problem? I would have thought Blowering going up and down by 80m was more of a headache.
To elaborate on the number of tunnels question: as far as I understand, frictional losses can be approximated using the Darcy–Weisbach equation. Given the same Darcy friction factor (which is approximately constant at these Reynolds numbers) , pressure drop due to friction per unit length is proportional to the square of the mean fluid velocity.
So keeping the proportion of frictional losses the same as in your TB proposal, the TT proposal uses two tunnels, 25km long, with ~85% of the total TB flow rate. 968e3 kg /s *9.8 m/s^2 * 670m = 6.3GW before losses, 5.4GW electrical power assuming efficiency of 0.85. The fraction of head drop due to friction is 3,3% in both cases, which seems pretty conservative (Darcy friction factor 0.015).
Essentially the point is that steeper tunnels are cheaper, because you can afford more losses per unit length and have the same overall efficiency.
I recalculated costs, rescaling costs in your table according to the number of tunnels, electrical power, and tunnel length where appropriate. I use the maximum head for the TB calculation.
Tantangara-Blowering:
8.3GW electrical
$7,170,000 total cost
$862/kW
Tantangara-Talbingo
5.4GW electrical
$3,440,000
$636/kW
Of course, these are based on your cost methodology, but it seems to indicate that TT is better. Especially since the proportion of tunnel cost (which is very uncertain) drops substantially. (I’m having trouble getting your figures to add up exactly hence the slightly different value for TB).
Hi dashpool,
I still haven’t had time to look back at the comparison of the four options so I am working from memory as to what I did at that time (about July or August last year). TB worked out to be the most economic option using the assumptions I used at the time. However, the anlaysis was very simple. For example I used the same size power station and equipment for all the options. I now realise that I need to double the size of the power station because the maximum size turbine and generator set is 750MW not 1500MW as I had used.
I’ll have a look again at my earlier calculations for the four options, but not until Monday.
However, I certainly would not dismiss the effect of using Talbingo for the lower reservoir for a very large pumped-hydro facility while also using it as the upper reservoir for Tumut 3. There will be significant compromises, efficiency losses, and costs associated with that. If the TT project was clearly economically viable, it might be at the expense of Tumut 3.
But as I said, this did not enter into my earlier calculations but was in the back of my mind.
@Lang: Given CSIRO predictions for AU rainfall to move down the isotherms away from the equator over the next few decades, I am surprised to see a pumped hydro calculation for AU that does not mention this.
I cannot recall whether you are an AGW denialist or not, but your Snowy study here seems compatible with believing that precipitation in south-east AU is and will be constant.
As you know, Venezuela depends heavily on hydro and due to drought is running blackouts and brownouts at present; Ecuador is 40% hydro dependent and had them from ca. last October to Jan.
While I believe that the Snowy contributes only ca 3.5% to the national grid, it would seem strange to build an addition to it the feedstock of which is migrating to the Pole.
Hi again Peter,
I am not sure what the efficiency losses would be when operating Talbingo as a middle station between two pumped hydro schemes. It seems like both schemes would tend to be operating in the same direction (either both pumping, or both generating) at any given moment. As a result, the variation in the level of Talbingo would tend to decrease. In the case where only one scheme is working, the variation would be no worse than before.
If anything this would appear to make combined operation easier, because:
1) It softens a volume constraint (height of Talbingo).
2) It slightly reduces the head variation of both schemes, so that equipment can operate closer to nominal head.
Both of these effects should be small though.
I look forward to seeing your updated costings.
@TerjeP, they haven’t even been able to get D-T fusion working. Not even with a fissionable blanket which provides a free 10x amplification of the energy released. Not even in a subcritical fission reactor with the neutron source being fusion instead of spallation.
p-B11 is orders of magnitude harder. I would expect it to take at least several decades just for the laser technology to improve enough between achieving ignition for D-T fusion at a useful pulse rate(~1 Hz could be useful if you have a large fission component, probably about ~10 Hz to make the economics work without fission) to p-B11 becomming feasible.
It’s becoming apparent that rainfall variability not only affects farming but hydro as well in several continents. Parts of western Tasmania got over 3 metres or 10 feet of rain last year I believe. This year I think those same areas have had less rain than Alice Springs. Assuming evaporation is minor it seems logical to utilise the sunk costs by looping the water flow in drought years. That is the river is almost dry but the dam stays full due to re-pumping. That also assumes the capital cost per watt is competitive.
If this volatility is systemic we might get a repeat of those times when peaking hydro was unable to prevent rolling blackouts in southern cities.
http://www.abc.net.au/news/stories/2009/01/30/2478497.htm?section=australia
The water was in the dams but the converters overheated on the Basslink cable. Next time the converters may be OK but the water won’t be there.
Another example of how climate change and population growth double up but the guvmints can’t see it.
John Newlands and Peter Lalor,
Rainfall is not relevant for pumped-hydro. The same water is pumped up and down between the upper and lower reservoirs. So pumped-hydro schemes have an upper reservoir that is entirely man-made, with no natural inflows.
In the case of Tantangara-Blowering or Tantangara-Talbingo, the inflows to Tantagara will make the scheme more economic than being dependent on pumped-hydro alone. I did not include the revenue from straight hydro generation in my calculations. The additional revenue would not be great, because most of the water captured by Tantangara must be diverted to Eucumbene for storage for use when most needed and when the peak power is most valuable.
The sentence in the second paragraph of my previous post was supposed to read “Some [not “so”] pumped-hydro schemes have an upper reservoir that is entirely man-made, with no natural inflows.”
Initially I compared four options, however I had not considered the Tantangara-Talbingo option previously. I have added it this morning. You are correct, it is better on a cost per kW basis. The key parameters and the cost of the four original options plus Tantangara-Talbingo are summarised below:
Power Storage Stg rate Cost Cost per unit Pw Cost per unit energy storage capacity
MW MWh MWh/h $ $/kW $/kWh
Tantangara Blowering 8,482 526,692 5,104 $6,689,079,648 $789 $13
Eucumbene Blowering 7,729 3,320,623 4,651 $8,336,829,648 $1,079 $3
Eucumbene Talbingo 2,140 24,946 1,168 $2,229,693,216 $1,042 $89
Tumut 3 Expansion 3,000 10,867 1,762 $3,597,948,848 $1,199 $331
Tantangara Talbingo 6,903 24,946 3,865 $4,022,349,120 $583 $161
The reviewers suggested that my estimates are low by a factor of about 2. I accept the reviewers comments; they have a lifetime of experience in hydro projects and are still fully involved. One is the Chief Engineer for a major utility with enormous hydro projects and still building them. The other is chief designer for another organisation and is on site building one in Asia now. We could not get a better sanity check from more experienced people than these two have provided. We can rely on what they have said in their reviews.
Let’s consider your most important concern about the costing for TT. You suggested we could manage with two instead of three tunnels. This is not correct. Let me explain how I did the simple analysis. The aim was to get a cost comparison. So I needed some detailed cost breakdowns by major components. The best available was for Tumut 3, a pumped-hydro facility built in about 1967. The cost breakdown for each major contract is available in the public domain. The costs from about 1967 and need to be escalated by about a factor of 10 to 2009 A$.
The Tumut 3 engineering specifications are also available. To make the comparison simple, I kept the rate of water flow the same for all options (except Eucumbene Talbingo where I used only one tunnel) and increased only the hydraulic head (or pressure). I assumed the power station, turbines, generators and length of steel pipe on the surface would be the same size for all options. Of course, this is a gross simplification. They should all be scaled up in proportion to power, (but not necessarily as a simple factor).
Many improvements are needed to my original estimates. The power station would need to be build below water level in the existing Blowering dam. That will be much higher cost than I allowed for. The upstream and down stream tunnels must be portaled below water level. The intake structure must be built below water level. These will add considerable extra costs. We would need a steel lined tunnel from the downstream portal to the position where the surface is some 400m above the tunnel level for TB and some 350m above for TT. I did not fully allow for the cost of the steel liner, nor for the logistics of getting the 12m diameter pipes from Sydney to Blowering. This may require high cost modifications to the highways from Sydney to Blowering. All these extras were no included in my estimate in the article published at the top of this thread.
What about the need for 2 or three tunnels for TT? The calculations are on the basis that the total flow is the same for all options and is the same as for Tumut 3. The total flow rate is 1133 m3/s. The flow velocity must be less than 3 m/s and preferably much less. One hydro project I worked on in Canada had a 2.8 km tunnel and the velocity in the unlined rock tunnel was 1.5 m/s. So, I have used the upper end of the acceptable velocity as the basis for the tunnel cross sectional area. So three tunnels are required and they are the same diameter for all projects, 12.7m (larger would be better from a head loss and revenue perspective). The head loss in the TB tunnel is 23m and in TT is 9m. This is a valuable benefit for the TT project, but I have not calculated the implications for total revenue and return on investment.
The last point concerns the impact of adding a 7GW pumped storage facility to the performance of the Tumut 1, 2 and 3 hydro system. I do not agree with you that the consequences would be insignificant. The scheme was optimised during design to obtain the maximum output and revenue consistent with meeting the obligations to provide water as required for irrigation. Water is released from Eucumbene to Tumut Pond and released down through Tumut 1, Tumut and Tumut 3 power stations. Some is held back below Tumut 3 and pumped back up at night into Talbingo. The remainder is released to Blowering where it is held for release to suit irrigation needs. Talbingo is designed to optimise the storage capacity above Tumut 3 so the best value can be extracted from that water. It is designed to hold the water pumped up by Tumut 3 at night and also to hold the flows released through Tumut 1 and Tumut 2. If all Talbingo’s stotrage was not required, its active storage would have been designed to be less. This would have given a higher maximum head and therefore more power in Tumut 3. The engineers knew what they were doing. We cannot add 7GW pump storage to that system without a significant impact on the operation and performance of the existing system. In my calculations, I have worked on the basis that 10% of the storage in Talbingo can be considered available for use by the new pump-hydro system.
At the moment I believe the Tantangara-Blowering pumped hydro facility would cost in the order of $13 billion ($1,577/kW) Tantangara-Talbingo pumped hydro facility would cost in the order of $8 billion ($1,165/kW). However, TB can store 527 GWh but TT just 25 GWh allowing for the impacts on the existing systems.
A more detailed comparison of the options would be needed to take this any further.
One option to be considered would be underground versus surface power station. The underground power station is much more costly, but it avoids much of the steel tunnel liner. This is as far as it is worth my while to take this simple options comparison.
dashpool and other contributors to this thread,
Further to my previous comments, I suspect none of these pumped-hydro schemes are economically viable at present. They may become viable if we adopt nuclear power. I expect some of these pumped-hydro schemes may start to be developed, in stages, once about half our coal fired power stations have been replaced with nuclear. I suspect pumped hydro will not be viable until we have a lot of nuclear installed, most of the coal is replaced and we are turning to pumped hydro instead of gas for the fast-response, load-following generation capacity.
dashpool
I am interested in this comment. I haven’t done the calculations for the cost of the steel liner, but if you could I’d be very interested.
Peter said:
And on this point I strongly suspect Peter has it right. It may well be that pumped hydro turns out to be the most cost-effective way of delivering increased power at short notice.
Fact is that pumped hydro is the ONLY solution that can be currently scaled, at a reasonable cost, and with a mature technology, to store excess nuclear power for peaking.
I suggest there are perhaps three ‘water’ connections for surplus nuclear electricity
1) pumped hydro
2) reverse osmosis desalination
3) high pressure electrolysis
A desal co-located with a coastal NPP could also expend electrical energy pumping the fresh water to a large holding tank in the hills above the city. That source can be mixed with conventional water supply when required. Electrolysis can produce compressed hydrogen and oxygen as a chemical feedstock and medical good respectively. These will be more expensively than hydrogen from steam reformed natural gas and oxy enriched air produced by the PSA method. However I have no doubt the demand for hydrogen will be insatiable in a few years.
Thus a large NPP could split the load between the grid, the desal and the electrolyser. I think they should be located together as a PR exercise and to reduce suspicions that the water and hydrogen output are underpinned by coal.
Dear Peter,
Your method for estimating costs (without scaling cost of certain system components for power generation, steepness or head height), and a very low figure for tunneling costs has led you to select a very large project which has extremely long tunnels and high head.
More accurate analysis might show smaller power plants to have comparable or smaller cost/kw.
I therefore am not confident that your system selection was correct. I don’t disagree with the referee’s comments though. I think that the cost estimates were too rough to say much except that pumped hydro would not be insanely expensive, even at quite large power. I don’t have the knowledge to provide better cost estimates, unfortunately. But it is an interesting exercise.
My gut feeling is that since large hydro has already been constructed in the area, with big tunnels, pumped storage should be feasible.
On flow rates: you seem to be claiming that a particular flow velocity is appropriate, without reference to the steepness or diameter of the pipe (based on previous experience). I would suggest that since the tunnels are very expensive, you had better figure out exactly how much flow you can put through the tunnel. Longer tunnels have more drag.
Data point: Jinping-II uses 4 headrace tunnels with nominal area of 100m^2 each (excavated diameter is 12.4m, but quite a lot of lining is required due to large overburden and water). At 4.4GW rated power (some sources give 4.8GW), efficiency 0.85, and rated head 310m (minimum head is 280m), gives a flow rate of 4.3m/s.
(www.rowa-ag.ch/images/PDFs/ref_JinPinStudie_d.pdf gives 4m/s)
We seem to both agree that the TT project would not interfere significantly with tumut scheme for the proposed pumping time.
On lining, 0.2m thick A517 steel would be sufficient for 8MPa pressure tube 12.5m diameter, at 30% of yield strength. That gives ~60e3 kg/m. At steel prices of a few dollars a kilo for simple steel products, plus assembly, transport, $250,000/m should be about sufficient. Liner thickness can decrease along the tube somewhat. To avoid transporting huge tubes, I believe that the liners are cut into sections, shaped so that welds are at a large angle to the line along the pipe. I am not a structural engineer, so this estimate is to be taken with appropriate caution.
Almost all high head hydro is built in caverns nowadays.
ps: Jinping II headrace tunnels are 17.2km long.
Hi dashpool,
Thank you for these comments and suggestions. This is much appreciated. I’ll provide a brief response to each.
This started off as a ‘ball park’ estimate. It is not a detailed cost analysis of all possible projects or options. It was confined to looking at the cost of adding pumped hydro to existing reservoirs in the Snowy Mountains Scheme. The initial proposal was to increase the capacity of Tumut 3 by a factor of two or three, including pumping back from Blowering. This was the least economic of the four options initially considered (in this rough comparison)
I agree that scaling up the power station, turbines and generators for the higher power will increase the estimated cost of all the options.
The slope of the tunnels is not relevant. The system may be designed with a near horizontal low pressure tunnel, shaft and high pressure tunnel or a sloping tunnel. Those are details that would be considered in preliminary design. They do not need to be decided during the earliest stages of feasibility. Regarding the “very low figure for tunneling costs”, I am not sure if you looked at the reference I gave you. This reference presents a compilation of world wide experience in all types of tunnels and rock conditions. The Swiss rail tunnel you pointed me to is not much help, unless we can separate out the costs for just the rock excavation component for the actual tunnels, excluding the tunnel lining, rails, signals, stations, cross tunnels, ventilation and rolling stock. All those appear to be included in the US$9 billion total project cost. Do you have the actual cost for the rock tunnelling? If so, can you point me to a link?
I agree that projects with shorter tunnels would be lower cost, everything else being equal. I am not aware of any other pumped hydro project that has tunnels as long required for these schemes. But this just supports the contention that these proposed pumped hydro projects, are not viable at this stage. I suspect this exercise supports the point, made earlier in this thread, that pumped hydro is not likely to be viable until a substantial amount of coal power is replaced with nuclear.
Small pumped-hydro projects are not viable either – without large subsidies.
My gut feel is that these projects are not economic until we have a major component of nuclear in the generation mix. If these projects were viable now, they would have been investigated extensively and repeatedly by now, and built long ago. They are not even on the radar. By the way, the water tunnels on the Snowy are not large. They are small span, and excavated by drill and blast – rough surface.
Practice for unlined rock tunnels for hydro schemes is maximum flow rate of 3m/s and usually well below that. The flow velocity, surface roughness and tunnel length are factors in the calculation of the head loss. The slope of the tunnel is not. The cross sectional area of the tunnel(s) is determined from the flow rate and flow velocity. The number of tunnels is determined by the excavation cost; larger diameters cost less per m3, but larger tunnel boring machines are less readily available and the mobilisations costs can be higher (eg modification to the highways from Sydney to Blowering).
I considered four configurations for the diameter and number of tunnels:
6 tunnels of 8.0m diameter, 3.76m/s = 401m head loss; cost $3.731 billion
3 tunnels of 12.7m diameter, 3.0m/s = 69m head loss; cost $3.295 billion
3 tunnels of 13.9m diameter, 2.5m/s = 43m head loss; cost $3.570 billion
2 tunnels of 15.5m diameter 3.0m/s = 35m head loss; cost $2.827 billion
I based the costs on 3 tunnels of 12.7 m diameter, because the tunnel boring machines for the larger diameters are less available.
I understand the Jinping-II headrace tunnels are lined. Therefore, they can have a higher flow rate than the unlined rock tunnels assumed for the T-B project. If the tunnels were lined they would be far more costly.
You have misunderstood my comments on that. I said the opposite.
Regarding the thickness of the steel plate for tunnel liner, did you look at the reference I provided on the design of tunnel liners (it is linked in the article above). The static pressure during pumping is 9.75MPa, not 8MPa. Also, I wonder, did you allow for dynamic internal pressure (when there is rapid shut off), for the external pressure and the buckling failure (see reference)?
You are correct that the steel plate thickness decreases from the portal to the end of the steel liner. The rate depends on the height of the ground surface above the tunnel. Let us assume the average thickness is 200 mm. We have three tunnels of 3 km length, 9,000 m @ $250,000/m = $2,250,000,000. That is 4.5 times more than I allowed in my estimate.
An underground rather than surface power station may be the better option. The cost of the steel liners would be much less; however, the cost of the underground power station is considerably more than the cost of a surface power station. The options would be compared during feasibility investigations. As pointed out above, this started as a simple exercise to get a rough cost estimate for the projects which were being claimed to be low cost and readily available. To get rough cost estimates I had to use information readily available. 33 year old costs are available for Tumut 3, a a pump storage facility with a surface power station, and located in Australia. That is a good start. World wide experience is that pump storage projects cost around $2000/kW.
Hi Peter,
Just to be clear:
I don’t think that your are exaggerating the cost of pumped hydro. I think your costs are too inaccurate to correctly select a project, or to give that much information about final cost. Thats why you end up falling back on ‘World wide experience $2000/kW’.
1) Tunneling costs:
You agreed earlier (8 April 2010 at 21.26) that the figure (fig 24 in reference) you used did not give all the costs. Also, it is not clear whether the tunnel is in ‘good ground’ or not. I don’t think you have a very useful number at all. Hopefully the part of the snowy mountains we are tunneling through is mostly granite, but who knows. I agree that the Gotthard tunnel estimate includes other things than tunneling, and the large overburden probably makes it more expensive: I intended it as a ‘high ball’ figure. Tunneling costs may indeed be a factor of two higher than this figure, rather than ~8 times higher.
Power station costs obviously need to be scaled with power to get even vaguely indicative figures.
2) Flow rates:
The ‘slope’ I am talking about is the overall slope (rated head)/(total length of tunnel). The point you seem to be missing is for the same tunnel efficiency [(head loss due to friction)/(rated head)] for otherwise identical tunnels, the flow rate will depend on the ‘slope’.
In other words 3m/s seems to be acceptable for a tunnel from Tantangara to Blowering, but if you were building the tunnel to Brisbane, the acceptable flow rate will be lower. If your tunnel to Blowering was 212km rather than 53km long, the acceptable flow rate for the same head loss would be ~1.5m/s.
Scaling your figures for TT, 25km tunnel for same flow rate gives 32m head loss. The efficiency of the tunnels alone is 95% (32m/670m), compared to 92% (69m/827m) for TB. So your TT tunnels are excessively conservative. I am not sure why we are having so much trouble engaging here: perhaps I am not expressing myself clearly.
3) Jinping II
These tunnels are lined for stability. I don’t know what the cost of lining a tunnel bored by a TBM in order to make it smooth would be. Certainly at an average thickness of 0.1m shotcrete material costs don’t look too bad.
Reference:
‘The hydraulic roughness of unlined and shotcreted TBM-bored tunnels in
volcanic rock: In situ observations and measurements at Kárahnjúkar Iceland’ by Kristín Martha Hákonardóttir et.al in Tunnelling and Underground Space Technology 24 (2009) 706–715
Unlined TBM walls 7.6m diameter, avg. 20mm roughness. Lined shotcrete walls, 10mm roughness. 10% difference in Darcy friction factor, 5% difference in velocity. for same head loss: conclusion, no, lined tunnels not significantly better.
4) Using 10% of Talbingo gives ~4hours of power and meets the original specification of 3 hours.
5) Lining: my figures were for 670m head TT where 8MPa seems adequate. I assumed that you wanted only 1km per tunnel, as per your cost breakdown. At 3km it indeed becomes very expensive. The pumps have to be buried deeper than (maybe 50m below) minimum dam level to deal with cavitation. So your turbines have to be at ~250m in altitude. Actually at this point it is clear that you are dealing with an underground power station anyway so this discussion is moot (same goes for TT obviously).
If you are designing a connection with 3km of 9MPa liner it indicates you are doing something wrong. By the way, where are your surface pipes meant to be? It seems like your whole design needs a complete rethink.
[…] Over at BraveNewClimate, there are some plans and cost estimates for a large (9 gigawatt) pumped hydroelectric storage facility in Australia. Two reservoirs separated by 875m of elevation would be joined with a 53km pipe. The […]
Dashpool,
Thank you again. You’ve made a lot of good points. Pity we didn’t have this discussion before I got started. I did not begin the exercise envisaging that I would get into this level of detail.
Below I will reply to the points in your latest post.
I agree with this statement. But ranking the projects was not the purpose of the exercise, as I explained in previous posts. In fact, the article did not include the rough analysis of the other projects. This was something I added in answer to one of your questions. What the exercise does show is that none of the projects are economically viable given the current mix of generators in the NEM. So it is no correct to claim that these pumped hydro sites could provide low-cost energy storage for intermittent renewables. It was that claim that the paper was originally written to address.
I used the world wide experience as a sanity check. It is unreasonable to believe that Australia has a pumped-hydro option sitting undeveloped in the Snowy Mountains Scheme, which would cost well below world experiece. If there was a feasible option SMEC and other organisations would have been advocating it for ages. It clearly is not viable.
I used “average tunnel costs” from the Evert Hoek’s figure 24, http://www.rocscience.com/hoek/references/H2001b.pdf. For the 12.7m diameter tunnel this gives a cost of A$155/m3 when escalated to 2009 A$. I could equally have used “good ground requiring minimum support” as that is the likely rock conditions for this tunnel. I’ve had some experience tunnelling in the area, am familiar with the rock types along the tunnel line, and have walked and done geological mapping in the area near Tantangara Dam and Long Plain. There is considerable experience and knowledge about the tunnelling conditions in the area. I have alos reviewed the 1:250,000 geological maps of the area which are available on-line from Geoscience Australia. I have written up a short description of the geology and rock conditions in the article. Having said this, if you can suggest a source of better cost figures for TBM tunnelling in granitic type rock, I’d be grateful. The Hoek figure 24 is still being widely used for preliminary estimating (that was confirmed by two of the people mentioned in the acknowledgements who are actively involved in underground excavation design and estimating, so I would need something more credible to persuade me to move away from these figures). I do agree that there may be some missing costs, and I may not have included sufficient escalation. However, the the TBM tunneling is cheaper and this would tend to reduce my estimate. However, all this is way beyond the level of detail I had intended to get into when I did the calculations initially.
I have just looked, for the first time, at possible tunnel alignments from Tantangara to Talbingo. This alignment will be a far more costly per kilometer than the Tantangara-Blowering alignment. For most of the tunnel length, the hydraulic head will be above ground level, meaning the tunnel will have to be lined as a pressure tunnel to prevent leakage. There are deeply incised creeks, where the tunnel will surface and have to be bridged, or the tunnel will need to be excavated at a relatively steep slope at the Tantangara end and then run at depth. The tunnel will pass through the limestones near Yarrongobilly Caves, meaning it may have to deal with cavernous limestones so there is the risk of dangerous, sudden water inflows during tunnelling. Furthermore, these sections would need to be lined as a pressure tunnel. From my rough scaling, I expect the tunnel will be more than 30km long, not the 20km you estimated. There is no suitable location for surge shafts. I expect the cost of this tunnel would be considerably higher per kilometer than the Tantangara-Blowering tunnel.
I agree I do need to scale up some of these costs, as I said before. I doubt the power station costs are proportional to power. The power of Tantangara-Blowering is six times higher than Tumut 3. However, I expect the costs would be perhaps 2 to 3 times higher than Tumut 3. I should have used twelve 750 MW instead of six 1,500 MW turbines, pumps and generators. The flow rate is the same as for Tumut 3 so I am guessing the turbines and pumps need only to be scaled up for strength, not flow. The generators should have been scaled up from 250MW to 1,500MW in my original estimates.
If I re-do the calculations, I would change from 6 to 12 turbines with half the flow rate of the Tumut 3 turbines and scale up from 6 generators of 250MW to 12 generators of 750MW. To do this I would reduce the cost of turbines to say 0.75 of the Tumut 3 turbines and increase the total cost of the generators by a factor of 4.5 of the total cost of the Tumut 3 generators.
The pumps are separate from the turbines in Tumut 3, but I understand would be the one unit in the Tantangara-Blowering power station (reversible Francis turbines used for both pumping and generating). So there is a cost saving for the pumps. I had included in my original estimates the factoring up of the pumping capacity.
I would double the size of the power station to cater for the 12 x 750 MW units instead of 6 x 1500 MW units (remembering that the turbines would have half the flow and therefore be smaller than the Tumut 3 turbines).
To keep this discussion in context, we are playing with power station costs that make up about 5% of the total project cost. The cost for the power station equipment in the article above totals $342 million. Roughly, I should double to tripple this to say $700 million to $1 billion. The total project cost increases from $6.7 billion to $7.4 or $7.7 billion (based on my initial figures). I’ve already accepted the cost of the project is more likely to be around $15 billion, so these changes are not very significant in the total picture. The component of the cost estimate I have the least confidence in is the steel tunnel lining.
You are expressing yourself clearly. I now understand your point. I felt previously it was a ‘down in the weeds’ issue so I had not examined it to this level of detail. The head loss in the 12.7m diameter, 53 km unlined rock tunnels for Tantangara-Blowering, I calculate as 69m..
Today I’ve looked at three options for the Tantangara-Talbingo (TT) tunnel. I’ve used 30 km tunnel length. Option 1 has three tunnels of 12.7m diameter, head loss = 39m. Options 2 and 3 keep the head loss the same as for Tantangara-Blowering (TB), i.e. 69 m. Option 2 has 3 tunnels of 11.4m diameter. Option 3 has 2 tunnels of 12.3m diameter. Now I see what you are getting at! 🙂
Tunnel excavation cost comparison:
TB with 69m head loss (3 x 12.7m x 53km tunnels) = $3.281 billion
TT with 26m head loss (3 x 12.7m x 30km tunnels) = $1.864 billion
TT with 69m head loss (3 x 10.5m x 30km tunnels) = $1.657 billion
TT with 69m head loss (2 x 11.4m x 30km tunnels) = $1.239 billion
The two tunnel option reduces the tunnel cost for TT by about $425 million. However, as pointed out above, I expect the cost estimates for the TT tunnels are too low in comparison with the TB tunnels. I expect they may be too low by perhaps 25% because of the reduced land height along the tunnel line, the need to cross deep ravines and the need for a pressure tunnel lining along much of the tunnel length.
Now I see what you were pointing out in your previous posts. Thank you. I didn’t take this into consideration when I ran the numbers for the TT option on Monday. I recognise there will be many other items that could also be improved for the purposes of comparing the projects. I accept your point that the rough figures I’ve produced are not sufficiently refined to allow a ranking of the projects. However, although the figures are not good enough to rank the projects, I still believe the exercise confirms that the projects are not viable with the existing generation system nor for energy storage for renewable energy generation such as wind and solar power.
3) and 4), I’ll skip over. Too much effort to explain any further. We can come back to these later if we want to get down to this level of detail.
The 9.75MPa pressure I gave was for TB and is for the maximum static head plus the friction loss. The dynamic head also must be added. You seem to know a lot about this, so I would be interested in what you would suggest. TB is the project I’ve done the main calculations on. As I mentioned in my previous post, I had not considered the TT option when I did the calculations last year (despite having said so in my first reply to you. My response was from memory). Monday morning I did a quick scaling to get the TT project. I have not analysed it to the same level of detail as I did for TB. However, for TT the maximum static head plus friction loss – when pumping from minimum operating level in lower reservoir to full supply level in upper reservoir – would be 763m.
I agree an underground power station might be the preferred option, but I do not have costs I can use. Without them, I cannot do the sort of ball park analysis I set out to do. I’d also point out that neither Tumut 3 nor Wivenhoe, Australia’s two largest pumped-hydro projects, have power statons. Both have surface power stations And neither go 50 m below minimum operating level.
The length of the steel lined section of the tunnel depends on the topography at the down stream end of the tunnel. The surface above the tunnel line does not get above above the Tantangara Full Supply Level until nearly 7 km from the downstream portal (see the east-west section of tunnel at the Blowering end of the tunnel).
I agree the design could do with a rethink. And, of course, that would be done as design progressed. The design for the orginal comparison was based on Tumut 3, as I’ve mentioned above. I had looked at surface penstocks at onstage and then settled on a configuration with surface pipes the same length as at Tumut 3, same diameter, and thicker steel for the higher pressure. I agree, if a surface power station was selected the configuration used at the Wivenhoe power station would be more suitable. There are lots of things to improved. I agree with many of your points and thank you for your contributions. This discussion is helpful for non-experts (of which I am one).
Main uncertainties in the cost estimates
1. Steel liner
2. tunnelling
3. underground versus surface power station
4. turbine/pump, generator and transformer
5. access and modifications to highways
Conclusion:
After all this, it seems the total project cost of around $15 billion for TB is unchanged.
I expect Tantangara-Talbingo would cost around $10 to $11 billion and have significant constraints on the amount of energy that could be generated without compromising operations in Tumut 1, 2 and 3.
We’ve been playing at the edges of the total project costs, except for the steel liner, which has a major uncertainty on the upside.
This rough analysis shows why these pumped hydro projects are not viable with the existing generation mix, and would not be suitable for energy storage for intermittent renewable energy. They may be viable once a substantial proportion of the electricity is supplied by nuclear power.
What next?
I am thinking of improving the calculations a little. I’d probably stick with a surface power station because I don’t have access to costs for an underground power station that I could scale up. I’d scale up the turbine/pumps, generator, transformer and power station as mentioned above and add some costs for the underwater work. If I could get better costs for tunnelling than Evert Hoek’s Terzaghi Lecture, I would use them, but I am not too concerned if I stick with Hoek’s figures and inflate them some more. The caption for Evert Hoek’s Figure 24 says: “Approximate costs for tunnel excavation and support (1999 US$). These costs do not include concrete lining, tunnel fittings or tunnels driven by TBMs.” Using TBM’s will be lower cost than drill and blast, so this will tend to offset tunnelling costs not included so far.
However, it is not worth my while re-doing the calculations unless I can get some help with the calculation for the steel costs. Would you be prepared to help me with that? I can provide the figures from two projects I used as the basis for my estimate. So, if I provide those figures, could you calculate the cost for the steel tunnel lining? I will recheck the length required.
Can I just say how interesting I have found the exchanges between Dashpool and Peter Lang! This is a fabulously informative set of posts especially for those of us interested in the potential of pumped storage to cost-effectively underpin clean energy systems.
Ewen,
Thank you for that comment. I am learning lots too!. I thank dashpool for his comments and hope he will continue to post here.
I mentioned the Wivenhoe pumped hydro project, near Brisbane, in my previous post. It is another example of a pumped-hydro project with a surface power station, albeit a low head one. Here is a fact sheet on Wivenhoe
http://www.tarongenergy.com.au/Portals/0/docs/factSheets/Factsheet%20-%20Wivenhoe%20Power%20Station%2024%20June%202008.pdf
I agree, thanks to Peter and dashpool for their incredibly informative comments (and to Peter for the lead post). This is ‘open blog science’ at its absolute best.
Dear Peter,
Thankyou for the informative reply. I don’t have that much more time right now, so I won’t post in that much detail and I will skip various points.
The point about underground pumping stations is that you can’t suck water uphill very far. Water head from bottom reservoir at pump intake + Atmospheric pressure has to be greater than zero. Because Jounama pondage varies only 9m in height, the pump intake at Tumut III could be built at 393m (max dam level) and still have positive intake pressure. I think actually it is built below this (by excavating a bit) but I can’t find the numbers.
So pumps at Blowering need to be built no higher than 10m above minimum dam level, 316m above sea level (actually somewhat lower than this to account for dynamic pressures in the pump). Since the ground next to the maximum dam level is at 380m, the pumps have to be significantly underground (or you could tunnel to the north side of the dam where the ground is lower, but this seems suboptimal).
On the cost of steel liners, I’m not sure I can do a particularly good cost estimate. I am assuming ‘typical’ steel costs and that material costs are around 50% of the total. Also (conservatively) assuming that the rock supports none of the load, which is reasonable for the thick part of the liner near ground level. In liners with similar internal and external pressures in good rock, the rock can support almost all of the hoop force and the liner, which acts like an elastic waterproof membrane, should be much cheaper (this is explained in the pdf on liners that you linked to). Dynamic pressures are typically limited to around 20% of the static pressures using protection devices like surge shafts and air chambers. (e.g. Applied hydraulic transients for hydropower plants and pumping stations By Mihail Popescu et. al)
Hi dashpool,
And thank you for your great replies too. Some readers are interested in the discussion so I’ll continue; the discussion provides readers with some insight into the sort of considerations involved in designing such systems. It provides insight as to why such systems are not as cheap as they often seem at first, and it illustrates the magnitude of the unknowns involved in the estimates. So here are responses to your post of 15 April @18:06.
I agree that pumps are normally submerged, but I was surprised by your comment about them being submerged by as much as 50m. I realise that this may be the case for an underground power station that is located a long way from the downstream reservoir, as this power station would have to be. Here are the relevant figures for Tumut 3 which is a ‘surface’ power and pump station (see the photo in the lead article for the thread):
Minimum Operating Level for pumping is: R.L.382.5
The centre of the pump scroll case is: R.L.362
The bottom of the excavation for the pumps is: R.L. 351
So the lowest point of the excavation is 32m below the Minimum Operating Level.
My original estimates for the power/pump station on the Blowering reservoir assumed the same arrangement as Tumut 3 (surface power station with submerged pumps), but based on the Blowering Minimum Operating Level, which is R.L.306. So the lowest point of the excavation would be at R.L. 274.
I agree that an underground power station may be more suitable, and this would be decided as design progresses. The cost of steel tunnel liner would be much less, but the cost of an underground power station would be more than a surface power station.
The Wivenhoe power station is also interesting for comparison. The lowest point of the excavation is 2m above seal level. It is a surface power station with similar arrangement to Tumut 3, but with two pumps and turbines. (vertical section: http://www.tarongenergy.com.au/Whatwedo/Generating/WivenhoePowerStation/Howelectricityismade/tabid/150/Default.aspx
Fact sheet: http://www.tarongenergy.com.au/Portals/0/docs/factSheets/Factsheet%20-%20Wivenhoe%20Power%20Station%2024%20June%202008.pdf
Steel Tunnel Liner Cost Estimate:
On the cost of the steel liners, I am not looking for a “good cost estimate” just an estimate that is an improvement on the very rough estimate I have now. My current estimate is based on scaling up from Tumut 3. I am still hoping you can help me to develop a better estimate for the steel liner. Below I explain how I estimated the costs for the steel surface pipe and tunnel liner by scaling from the Tumut 3 pipe costs. Following this, I list steel pipe dimensions and static hydraulic head for two projects and scale these up to estimate steel thickness for pipe at surface (no support from rock mass) and for tunnel (with support from rock mass). Lastly, I provide some input assumptions for the tunnel liner analysis. I am hoping you may be able to run this analysis for me, as I no longer have access to a program to do this, and am not particularly interested in doing the calculations from scratch or writing a spreadsheet or program to do them. I‘d be happy to ignore the analysis for the external pressure failure mode if that makes it easier.
1) Steel costs scaled up and escalated from Tumut 3 steel costs
The contract for the steel pipe for Tumut 3 was for $8,100,000 in 1968.
Escalate to 2009 $ = $81,000,000.
Surface pipes: factor up in proportion to maximum static pressure and pipe diameter = $495 million.
Tunnel liner: factor up in proportion to tunnel length and estimated steel plate thickness = $498 million.
Total cost of tunnel liner and surface pipes = $1 billion (approx.).
2) Steel thickness at surface scaled up from Tumut 3
Tumut 3:
Maximum static hydraulic head 155 m
Pipe diameter 5.56 m
Steel plate thickness, top 19.0 mm
Steel liner thickness, bottom 30.0 mm
Tantangara-Blowring:
Maximum static hydraulic head 993 m
Pipe diameter 11.12 m
Plate thickness scaled in proportion to head and diameter:
Steel plate thickness, top 243 mm
Steel liner thickness, bottom 384 mm
3) Steel thickness at surface and in tunnel scaled up from Cat Arm, Newfoundland, Canada
http://www.nlh.nl.ca/HydroWeb/NLHydroWeb.nsf/LookupGeneratingFacilities/Cat%20Arm%20Hydroelectric%20Generating%20Station?OpenDocument
Full Supply Level (R.L.) 393.2 m
Turbine Level (R.L.) 6.7 m
Static hydraulic head 386.5 m
Tunnel length 2,800 m
Unlined length 2,374 m
Steel lined length 426 m
Tunnel height and width
Unlined section 5.6 m
Lined section 4.2 m
Steel lined tunnel, inside diameter 2.9 m
Flow rate 40 m3/s
Flow velocity (unlined section) 1.5 m/s
Flow velocity (steel lined section) 6.1 m/s
Steel liner thickness, in tunnel (20m to 426 m from portal) 25 mm
Steel liner thickness, at surface and 0 to 20m from portal 75 mm
The steel pipe thickness is 75mm at surface and this is continued to 20m into the tunnel; then reduces to 25mm for the remaining 406m of the steel lined section.
The Cat Arm tunnel is in granite throughout. The rock is unweathered right to the ground surface (weathered overburden removed by ice sheets during ice age). This is a different situation to Blowering where the rock mass would be weathered, to varying degrees, to perhaps 50m depth (more in places).
Importantly, at Cat Arm the ground surface rises steeply to half the hydraulic head by 400m horizontally in from the tunnel portal. The end of the steel liner is below the point where the ground surface is at about 145m elevation, which is half the hydraulic head.
Scaling up the thickness of the Cat Arm steel liner to Tantangara-Blowering by the ratios of diameter and pressure would give:
Cat Arm, Tantangara-Blowering
75mm, 740mm
25mm, 246mm
My rough scaling is giving a steel thickness for the Tantangara-Blowering tunnel liner of about 246 mm, which is about 25% more than the 200mm you suggested. Scaling up the surface pipe to the Tantangara-Blowering pressure gives a steel thickness of 384mm based on Tumut 3 or 740mm based on Cat Arm. I don’t understand why this massive difference. (Perhaps it is because Cat Arm is 2.8km tunnel with no surge chamber whereas Tumut 3 penstocks are only 488m. Do you have any thoughts on this? What steel thickness would you calculate is necessary for 9.75MPa static pressure in an 11.12m diameter pipe?
4) Inputs for Tunnel Liner Analysis
Today, I have more carefully read from topographic map the ground level above the tunnel line at the downstream end. Having now done this more carefully than originally, I find the steel liner would need to be about 1.5 km long. I have also calculated vertical stress in the rock mass and given some very rough estimates of horizontal stress perpendicular to the tunnel at various distances from the tunnel portal; see below:
Tunnel distance from portal m 0 444 1333 1444 1667
Ground surface (R.L.) m 380 500 750 800 850
Tunnel level (R.L.) m 380 382 388 393 400
Cover m 0 118 362 407 450
rock mass unit weight kN/m3 25 25 25 25 25
Vertical stress MPa 0.0 2.9 9.1 10.2 11.3
Ratio horizontal to vertical stress 5 4 4 4
Horizontal stress MPa 14.7 36.2 40.7 45.0
Rock mass deformation modulus GPa 0.2 0.5 0.5 0.5
5) Estimating tunnel liner costs
You mentioned that your estimate of steel costs assumes the material is about half the cost. Do I understand correctly you have factored up the cost of steel materials by a factor of 2 to cover for transport and installation. Would this figure include the cost of the backfill concrete and grouting? This is a tricky issue, as you is know. The concrete and grouting must avoid a crack forming between the liner and the concrete. The steel liner may be installed when air temperature in the tunnel is, say, 25C. When the water enters from Tantangara dam it may be as cool as 4C. The steel liner may shrink and pull away from the concrete causing a crack between the steel and the concrete. If the tunnel is dewatered, external water pressure can cause the steel pipe to buckle inwards. So the grouting around the steel liner is an important issue. My questions is, do your costs for the steel liner include the installation of it in the tunnel, including the grouting?
Summary of my questions:
1. Can you give me a better estimate of the tunnel liner steel thickness, using the inputs I have provided?
2. Can you give me a rough estimate of the cost per tonne of steel (installed cost)? With this I may be able to adapt it to other options.
3. Can you give me a rough estimate for the cost of tunnel liner, per linear meter, and per steel thickness? I ask for this because I expect the length of the sections of different thickness may change depending on the ground surface profile.
4. What steel thickness would you calculate for 9.75MPa static pressure in a 11.12m diameter pipe on the surface?
5. Do I understand correctly you have factored up the cost of steel materials by a factor of 2 to cover for transport and installation. Would this figure include the cost of the backfill concrete and grouting?
Dashpool, I look for ward to your responses.
Dear Peter,
It seems to me that by excavating a 106m deep hole (from maximum dam level of 380m to 274m at the bottom of the pumps) you have more or less built an underground power station anyway.
Anyway, I think this is about enough of the details for me. I might say something about the liner later if I get time.
Hi dashpool,
Thank you for the comment, and I hope you do get a chance to look at the tunnel liner costs. As I mentioned before, I am not disagreeing that the underground power station might be preferable. However, I have nothing I can use as a basis to estimate the costs. There are costs and savings for both options, and many other options too, that would be considered in the options analysis. As you would know, open pit excavations ar far chepaer than underground excavations. As I said, if you have figures I could use for the underground powerhouse option, I’d be most please to work with them. Without some figures, I cannot progress the underground option.
dashpool,
I’ve been excessively conservative with my ratio of horizontal to vertical in situ stress in the rock mass. Halve the ratio and halve the horizontal stress.
Have you heard of this other method of pumped hydro proposed by Gravity Power in the US? Here is a link to an article about it published in ‘International Water Power and Dam Construction’.
http://www.waterpowermagazine.com/story.asp?storyCode=2056045
Any thoughts on their approach versus your approach?
Peter – vaguely related question: whats the power and energy capacity of the Snowy scheme, ie x GW for y hours?
Second question – Tumut 3 has 1.5 GW generating capacity – how long can it provide this for?
I know you’ve discussed these figures before, but it would take forever to hunt through the discussions to find them.
Cindy Waldorf,
Thank you for this article and for your question.
I had not heard of this concept. Here are a few initial reactions:
1. It is in early R&D stage. Most such ideas do not become commercial. Even those that do, take decades. Large systems, such as energy generation and storage, have a life expectancy of 20 to 80 years and are very expensive, so no one will build them at large scale until proven. That means a very long time until they become commercially viable at the scale needed to make a significant contribution to electrcity supply.
2. We have been ‘playing’ with pumped-hydro in deep mines for some time. This can be viable in some cases, but the amount of energy available is relatively small compared with conventional pumped-hydro, which connects surface reservoirs with much larger volume of water storage.
3. The fundamental physics cannot be bypassed. That is, power = weight of water per second, multiplied by height. So, for large power we need a large volume of water falling a great height. And we have to pump it back up again at night. So the round trip efficiency is important. Currently, pumped hydro is around 75% to 80% efficient, depending on the specific site conditions. Any new system needs to beat that, or be much cheaper over its life for other reasons.
4. Whereas there is a lot of room to improve the efficiency in coal, gas and nuclear generation, there is very little room for efficiency improvements in hydro-electric. Conventional hydro is a mature technology. It will take something very special to beat it. Whereas coal fired power plants range from about 20% efficient (Hazelwood, Victoria) to about 37.5% efficient (Millmerran and Kogan Creek, Queensland), hydro-electric is about 95% efficient (this refers to hydro-electric generation not the round trip efficiency of pumped-hydro).
5. The proposed system appears to have moving parts. I expect it will be very difficult to bring such a system to maturity and for it to have a long reliable life.
6. Excavating shafts is a very costly process – much more costly that tunnelling.
7. I notice this is being proposed for Texas to attempt to make the wind farms viable. My reaction is we are trying very hard to make wind farms viable. ‘You can’t turn a sow’s ear into a silk purse’. I’d suggest we simply dispense with the forlorn hopes of making renewables viable, dispense with the fear of nuclear and get rational.
8.
That is not special. Hydro-electric response time is very fast already. Dinorwig pumped-hydro station in Wales can ramp from 0 to 1800MW in 75 seconds, and that is from all turbines stationary, not spinning. Usually some are kept spinning to allow much faster response time.
9. Some important questions are not addressed in the article:
a) What is the expected cost (per kW and per kWh capacity, and per kWh cost of electricity).
b) What is the life expectancy
c) How long does it take to change from generating to storing. If this is a short time, then that ould give this system an enormous advantage over conventional pumped-hydro for storing energy from intermittent renewable generators.
This looks to me to be another Silicon Valley scheme to get venture capital and make a few guys rich quick:
John D Morgan,
From: http://www.snowyhydro.com.au/levelOne.asp?pageID=3
The installed capacity is 3,800MW
It produce 4,500GWh per year on average.
That is a capacity factor of 14%.
Over the long term, the amount of energy that can be generated from the existing installed capacity (i,e. without adding new installations) depends on the amount of water inflow to the dams. Over a short term, water can be withdrawn from storage to generate more energy than the inflows would allow. (This is equivalent to spending more than your income by drawing down on your bank accounts.)
To answer your specific question about the energy: theoretically, 3.8GW for 1184 hours per year. We could, of course, drain the dams and get more energy as a once off. How much more would depend on how full the dams are. They are not very full at the moment, thanks to the long drought.
Peter Lang this raises the prospects that Australian hydro will henceforth chronically underperform if we are in a long term drying trend. On a recent bushwalk I was tempted to shortcut through the transformer station on a small (12MWe) unattended hydro in Tasmania. I was surprised at the low dam level given 2009 was a very wet year. I speculate that is due to chasing spot prices for peak power via the Basslink cable then re-importing cheap coal from the mainland.
Thus I wonder if we should keep the dams topped up even in chronic drought years as a kind of peak power battery or capacitor rather than a source of steady power. However I’d like to that to be backed up with disincentives to burn gas instead as I believe gas should be conserved for other long term needs.
Peter,
It’s a very serious effort, backed by employees, investors and strategic collaborators who know how to sink shafts, design and develop pump-turbines and roll out projects. You should not be short-sighted in your assessments or at least request further information. We support all forms of pumped hydro, big and small, because we need it. Also, the water does not create head; it only does the work.
BTW, we’re not in Silicon Valley.
Chris
Chris – who cares if it serious effort, backed by employees, investors and strategic collaborators, Peter raised some good points, answer them if you can, but don’t call anyone short-sighted because they don’t by into this idea without some questions.
John D Morgan,
Thank you for this and the previous excellent questions. They are very relevant to the previous discussion with dashpool. The relevance is to my argument that we cannot simply add a very large pumped hydro scheme that uses the top reservoir of Tumut 3 without compromising the operation and economics of the Tumut river hydro development, and especially the Tumut 3 component of the system. Dashpool disagress with this. I may write another comment to better explain my argument.
Now to answer your question:
If Jounama Pond (the reservoir below Tumut 3) is at Minimum Operating Level, then it will take 6 hours to fill with Tumut running at full power, 1500MW. (it would take 21 hour to pump the water back up from Jounama Pond to Talbingo Reservoir)
After that, water is spilled from Jounama Pond into Blowering Reservoir and cannot be pumped back up. (However, the Tantangara-Blowering pumped hydro scheme would use this water that would ortherwise be lost from the hydro-electric system).
If Talbingo is at Full Supply Level, no water is being released from upstream (through Tumut 1 and Tumut 2) and we allow the water to be lost from Jounama Pond once it is full, then Tumut 3 can generate at 1500 MW for 44 hours.
Just for clarity, the relationship of the reservoirs and power station are, starting from upstream:
Talbingo Reservoir (upper storage)
Tumut 3 Power station and pump station
Jounama Pond (lower storage reservoir)
Blowering Reservoir – catches all the water flowing down the Tumut River after it has passed throuugh Tumut 2, Tumut 2 and Tumut 3 and has spilled from Jounama Pond.
The main purpose of Blowering Reservoir is to hold the water that has been used for generating power and release it when and at a reate required for irrigation. As such the water in Blowering needs to be managed for the long term to ensure adequate water supplies through long periods of drought. As water is released from Blowering it generates power, but that is a secondary consideration in deciding when and how much water to release from Blowering Reservoir.
Blowering has a large storage capacity, so adding the Tantangara-Blowering pumped hydro facility would not compromise the operation of the Blowering Reservoir.
Hi Chris,
Thank you for your comment. I agree, we all need to keep an open mind on new developments. I read the article quickly. I had nor heard of this particular new development previously. I found the article difficult to understand. It makes little sense to me. If you could post a link to another, clearer artilce, I am sure many here would be very interested.
For me, without good costings, I cannot get very excited about the many thousands of proposed new solutions that pop up everywhere.
The cost of excavating shafts is very high, so I have trouble believeing that this could be viable. Pumped hydro where the shaft has already been sunk for existing disused mines, are marginal at best. So I’d need some good costing information to get me excited about this.
John Newlands
I agree. When the state and Federal governments were intent on privatising Snowy Hydro, the accounts took over the management of Snowy Hydro. They instructed the operators to generate as much power as they could to make the profit and losss look good. They emptied the reservoirs (an exaggeration but you get the picture). They sold off assets (stored water) to make the business look more profitable than it actually is on a sustainable basis. That’s what accountants do when they want to sell something!!
In principle I strongly agree with this statement. Especially, I agree : gas should be conserved for other long term needs”. However, without trying to start this disussion all over again, I believe the way to achieve this objective is to remove the distortions that are causing us to have to burn gas. If we had the option of nuclear for baseload power at the cost it should, and could be if the distortions were removed, then we would not need to burn gas over for electrcity generation. However, I do agree we will need to burn gas until the time when we have a substantial proportion of our electrcity generated by nuclear. Then we can start winding back on the amount of gas.
The approach should be to remove the distortions that are causing nuclear to be costly, rather than add more distortions to the cost of coal and gas (other than internalising externalities where this can be done properly across all industries in a properly comparable basis and the benefits outweigh the cost to the whole community).
Thanks Peter for your clear and detailed response. Having your expertise available here really is a tremendous asset.
I am responding in the discussion thread in Crikey to Eponymous, who has referred to Australia’s 2.5 GW of pumped hydro storage. I am not sure he realizes the limits on that 2.5 GW, hence my question to you. Thanks again.
John,
I’ve mentioned in previous posts, but it is an important point to try to get across to those who think pump storage can help intemittent renewables, it cannot.
Renewanbles provide intermittent power, it is expensive, and it is not reliable in the early hours of the morning when we mucxt pump. The reason we need to pump in the early hjours of the morning, not during the day, is because the demand is lowest in the early hours of the morning. We can’t pump at other times because that is the times when we need to be generating power.
Wind power costs about $110/MWh + $15/MWh average fro transmission. So all up about $125/mWh. (by the way, the $15/MWh is one of the externalities that are not being attibuted to the wind generators).
For pump hydro to be viable they need to buy electricity in the early hours of the morning at about 1/4 the price they can sell it for. Coal and nuclear provide cheap off-peak power in the early hours of the morning (at around $20-$30/MWh, so they can provide the cheap power to allow pumped hydro to be viable. Clearly, wind cannot do this, and solar is not much help in the early hours of the morning (sarcasm alert).
The third factor is that for pumped hydro we need reliable, constant power for the pumping hours.
Wivenhoe, a 500MW pumped hydro facility near Brisbane, pumps from midnight to about 6am (average 5 hours). It supplies to meet peak load for about 7 hours per day (not at full power most of the time), and is on standby for 12 hours per day. During standby it provides some power to stabilise the grid. Your readers should understand from this, that pumped hydro is not available for pumping during the day time, Pump-hydro cannot quickly change to and from pumping. The weight of water in the pipes must be accelerated each time you start pumping. For Tumut 3, the pipes are 5.56m diameter, 448m long the water must be lifted 155m.
Thanks Peter, thats a very helpful summary of the issues.
I probably won’t raise most of this in the Crikey thread unless it comes up again as it seems to be beyond the sophistication of that discussion, which is very much zeroth order analysis. But I now know its here in this pumped hydro thread.
Incidentally, that discussion seems to be running quite strongly against renewables. We must thank Mark D for providing a great platform for the critique.
Peter/others:
I do have to say this is one of the more intelligent blogs on the subject we’ve come across.
Gravity Power has two markets for its system; the first being a capacity market, the second market being an energy market. We’re estimating about $1200/kW for the initial systems designed to be about 7.5MWh of storage capability each. With the ability to be more flexible in our siting vs. large PSH, we select competent rock, not too hard, but stable, thus reducing construction risk and costs. We’re using a shaft sinking method and facility layout that allows a unique combination of tried and true methods and a slant on a horizontal method. Believe me, we’re well aware of the conventional shaft sinking expense, having talked to many of the contractors that specialize in these things. Recall most shafts are relegated to a site (ore, ventilation, etc.) and thus there is no ability to choose the geology. Plus, does anyone do multiple shafts in close proximity? That helps amortize equipment, commonize use of conveyance and optimizes logistics of shipping commodity materials to sites. Peter, I’ll see if I can dig up more publicly available materials and in the meantime, thank you for your interest.
Chris
Peter,
Thank you for your response to my question and for your willingness to participate in this discussion in such an informative and productive manner. Your time is very much appreciated and thanks for sharing your expertise with a broader audience. I wish there were more online discussions like this.
Peter’s analysis on Renewables with pumped hydro is clearly skewed, wrong and misleading.
If your renewable grid has a lot of short term storage, ie 18hours with Molten Salt Power Towers, combined with weather forecasting it is easy to provide consistently many hours of pumping when that is the requirement.
Trying to compare the variability of 1 solar site (with no storage) or 1 wind site (with no storage) and then applying that to the lead time to switch from pumping to generating is cherry picking and trying to create a scenario that would never eventuate for the sake of your argument.
But I suppose that supports your pro nuclear agenda so it makes sense in that context.
Other than that – good numbers on pumped hydro, and I will get my research team to have a look and see where else we can go with them.
Matthew, how does 18 hours storage on the generators provide power for two or three days of cloud at synoptic weather scale? Even with forecasting?
Mathew Wright,
Thank you for your comments.
Do you have actual figures to support this statement?
There are several adjectives here that are not quantified. What is “a lot of short term storage”? What are you comparing with? What is “many hours of pumping when that is the requirement”?
You might like to look at this to explain one end of the spectrum: http://bravenewclimate.com/2009/08/16/solar-power-realities-supply-demand-storage-and-costs/
And this on solar thermal: http://bravenewclimate.com/2009/09/10/solar-realities-and-transmission-costs-addendum/
Where do we have 18h molten storage power towers in commercial operation? What is the cost of electricity from these? Surely, when we are using the stored energy from molten salt storage for supplying power to the grid we can’t also be using it for pumping, can we?
Where did you get the idea that I was comparing the variability of 1 solar site or 1 wind site? I wonder if you have read the papers ‘Solar Power Realities’, ‘Solar Realities and Transmission Costs – Addendum’ and ‘Emission Cuts Realities’. The papers are available from here: http://bravenewclimate.com/renewable-limits/
I recommend clicking on the link to the pdf version in each case.
I get the impression you may have missed these replies: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-52905
and here:
http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-58646
These charts show the variability of wind power in the Australian National Electricity Market: http://windfarmperformance.info/ . Select a month from the list on the right.
This comment suggests you have an irrational agenda. However, if you want to discuss this further, I’ll happy to.
I’d be very interested to hear your explanation of why you believe pumped-hydro provides economically viable energy storage that makes wind and solar power economically viable on a large scale. I look forward to your explanation.
Australia’s Pumped Hydro energy storage capacity
I’ve been asked elsewhere how much energy can be stored in Australia’s existing pumped hydro schemes. I have looked at only the two largest.
Australia’s two largest pumped hydro facilities are Tumut 3 and Wivenhoe. The rated generating capacity is: Tumut 3 = 1500MW, Wivenhoe = 500MW.
See aerial photo of Tumut 3 here (figure 7) http://www.rise.org.au/info/Tech/hydro/large.html
The smaller of the upper and lower reservoir for each facility defines the energy storage capacity.
I calculate the following:
Tumut 3 can generate at full power (1500MW) for 6.8 hours before the lower reservoir overflows (assuming it is at Minimum Operating Level at the start). That is, 10,867MWh of energy. However, Tumut 3 can store only 2,642MWh of energy in 6 hours of pumping each night. Therefore, Tumut 3 has 2,642MWh of energy storage capacity per day on an ongoing basis. Put another way, it would take four nights of pumping at full power for 6 hours to enough energy to generate at full power for 6.8 hours.
Wivenhoe can store 1,726MWh in 5 hours of pumping per day.
Therefore, the total energy storage capacity, per day, of Australia’s two largest pumped hydro facilities is about 4,300 MWh per day.
The significance of these figures is that the amount of energy storage we have is going to be next to useless as far as helping wind to provide our power through a period of low or no wind, or solar to provide our power through the even one night, let alone several nights. To put these figures in perspective, we need 450,000MWh of electricity, from somewhere, to meet our demand for one night. Our current energy storage could provide about 1% of our needs.
Conceivably a dam could be its own upper and lower reservoir if the small outfall pond from the turbine hall was immediately pumped uphill to the lake. This would be a kind of reverse alpenstock incorporating pumps only. Those pumps could be variable speed if the power source was intermittent and unregulated.
This is not so far fetched as I already pump water between a pond and a slightly elevated tank in the vegie garden. Admittedly with 12v solar panels it cost $15 a watt not counting the batteries.
Let me turn the problem around by posing this problem; is there anything that can be done to justify installing the two 144 MW Francis turbines in the vacant slots at the chronically low Gordon Power Station? I believe NSW, Vic and Tas each have dams that are chronically low and could be said to underperform.
John,
I don’t really understand your question. However, you can do the maths. The area that needs to be innundated and the height difference between the top and bottom reservoirs are enormous to get a reasonable amount of power.
Look back at the lead article for this thread. This enormous pumped hydro scheme, by far the largest in the world, would generate 8,000 MW of power and store about 40,000MWh each night, between midnight and 6am. That is about 6% of the daily electricity consumption of the NEM. In most cases small hydro schemes are uneconomic unless heavily subsidised.
A large pumped hydro schemem like the one described in the lead article, would be valuable and viable if linked with a substantial amount of nuclear power in the NEM.
I’m not sure how to calculate the costs but I picture unregulated wind generators on ridges or coastlines near half full hydro dams. Via short cheaper transmission lines variable speed external pumps return the dam outfall water to the lake recovering perhaps 80% of the input power.
This avoids the costs of wind output regulation, grid integration and backup. The only grid interface is the existing one at the hydro. If southern Australia is in a long term drying trend low level dams may become a common sight. Some of those dams will be close to good wind sites. For example in Tasmania there is a small Lake Echo hydro and 5km away there is to be a large Lake Echo wind farm. Perhaps the wind farm should stay off-grid and the hydro modified to function as its power smoother, in effect a capacitor. I don’t know if cost savings and extras will cancel out.
John Newlands,
This is the problem. They don’t.
Let’s consider this from the big picture perspective to start with. Wind power costs about $2600/kW in Australia. Large pumped hydro about $2000/kW. Small pumped hydro costs more. Wind capacity factor is about 30%, so say we need 3 kW of installed capacity of wind to equal 1kW from an NPP or fossil fuel plant. Plus we need say 10 days (240 hours) or more of energy storage if wind is the supplier versus about 6 hours storage if NPP or coal is the supplier.
Put it al together and I expect the cost of electricity from a scheme such as you are proposing would be perhaps 5 to 10 times the cost of electricity from an NPP.
You also need to consider where you can find suitable sitres for pumped hydro. If you give me some figures for a site you have in mind, I’ll tell you how much power it can produce and how much energy it can store. the inputs we need are:
1. Hydraulic head (the difference in elevation between the top reservoir at its Minimum Operating Level and the lower reservoir at its Full Supply Level)
2. The active storage of the smaller reservoir.
3. The flow rate you are assuming in the pumps during pumping and the turbines when generating at full power
You can do the calculations yourself.
Power (W) = hydraulic head (m) x flow rate (m^3/s) x density of water (kg/m^3) x 9.81m/s^2 x efficiency.
Energy storage capacity = hydraulic head (m) x volume of smaller reservoir (m3) x density of water (kg/m^3) x 9.81m/s^2 x efficiency.
For generation assume the efficiency is 90% to 95%. Assume the round trip efficiency is 75% to 80%.
In the case of the adjoining wind farm and hydro I suggest the following. The 225 MW nameplate wind farm may have an average output of say 60MW. If the 32 MW hydro is say 10m deep then it flows 327 cubic metres a second assuming perfect efficiency. Put in a new turbine with 92 MW = 32 + 60 capacity. We want the dam raised to say 15 metres high with a flow of 626 cubic metres per second. Knock off 20% and we will get a smoothed average 48 MW from the 225 MW wind farm (21% capacity). However there are no direct grid connection costs since the wind output would be unregulated but the dam would need to be modified.
However I note in practice the wind output will be sent to a substation which collects from several hydro stations. Perhaps they will integrate wind by throttling back hydro input. This would require wind output variation smaller than can be shadowed by hydro. Presumably a wind surge that was not needed by the grid will be restricted. With direct pumping that wind surge would be saved.
John,
I started to look at the figures you provided, but didn’t have all the info I’d need. So I’ve provided a second way to address your question
Comments on your analysis
I’ll use your figures without checking the cals. You require 327m^3/s. At 3m/s flow velocity, we need pipes with a cross sectional area of 109m^2. What is the cost of these pipes. Then we have the cost of the mechanical and electrical equipments and civil works. I’d allow $3000 to 5000/kW on top of the $2600/kW for the wind farm. We need to be able to accept the full installed capacity of the wind farms.
We also need to work out the area of the top and bottom reservoirs to hold say 10 days of stored energy. I suggest you have a go at this. I could do it for you, but I don’t think you will accept what I say until you have a go at the analyses yourself.
Remember that the power is calculated on the difference between MOL in the upper reservoir and FSL in the lower reservoir. So if your active storage is say 5m depth, and you want 15m head, the FSL in the upper reservoir will be 20m above the FSL of the lower reservoir and 25m above the MOL of the lower reservoir. Then you need freeboard above the FSL. Having a go at costing this scheme.
Another approach
We can consider two options:
1. The wind power is fed into a pumped hydro site as you suggest.
2. The power from the wind farm is fed into the national grid.
Let’s look at these in more detail
1. The wind power is fed into a pumped hydro site as you suggest. The pumped hydro site has to be developed, or an existing site enhanced. The pumped hydro site would need to be able to accept the maximum output of the wind farm, 225 MW, but the average power that could be stored and sold would be only 48MW (you estimated the average power supplied by the wind farm would be 60MW and we’d get about 80% of that back from the pumped hydro plant). So we would be building a 225MW hydro plant to generate and sell just 48MW average power. Not promising!
2. The power from the wind farm is fed into the national grid. If the power is fed into the grid, and the transmission system is sized to carry the maximum output of the wind farm, then all power produced by the wind farm can offset hydro power that would otherwise have to be generated from hydro. So in effect the hydro energy is stored by not using the water that is stored in the reservoirs. This is clearly the least cost solution because we don’t have to develop the pumped hydro site. And why would we want to. There is no benefit. In fact 20% of the energy would be lost through efficiency losses. Where hydro is available to back up for wind it is an excellent match and may (in some cases) make wind power economic where it wouldn’t otherwise be. This is what DV82XL pointed out is the situation in Quebec. It is also the situation with Denmark and Norway. Denmark sells its wind power to Norway for near nothing then Norway and sells it back to Denmark at peak power prices. Or Denmark buys baseload power from France’s nuclear power plants. Either way, the Danes are paying massively for their renewable dream.
So there is no real point in pursuing option 2 unless you want to. I expect it would be a very high cost option.
Peter at this stage my knowledge of hydro is not sophisticated enough to do these cost calculations. However I envisage only a small bottom reservoir at the outfall that wouldn’t be sucked dry. Even if direct wind pumping was viable at selected sites it would barely make a dent in coal burning.
I wondered if the US had thought of direct wind pumping to address the possibility of Lake Mead becoming unusable within a decade. Direct wind pumping could enable some hydro to function perhaps not downstream irrigation. The thinking seems to adapt to highly variable flows
http://www.brighterenergy.org/9098/news/marine-hydro/hoover-dam-turbines-set-for-upgrade-to-cope-with-drought/
John Newlands, on 11 May 2010 at 6.33 Said:
John, we don’t need a sophisticated understanding of hydro to compare these options. We just need to do a simple comparison. There are two key comparisons both of which make the decision crystal clear. One is the comparison of the capital cost per kW for the two options and the other is the amount of storage you need in the smaller reservoir.
For the option of wind feeding into the grid the capital cost per average kW is $9,750. For the option with wind feeding into the pumped hydro scheme and then into the grid the cost per average kW is $26,500. The pumped hydro scheme is much higher cost and provides no significant benefit in a system where there is already plenty of hydro capacity, and storage, in the system, as you have in Tasmania.
Capital cost per average kW.
Option 1 – If wind power is feeding into the grid then the Capital cost per average kW is $9,750/av kW.
(This is calculated as follows: 225MW capacity, 60MW average power (your figure), Capital cost = 225,000kW x $2,600/kW = $585 million. Capital cost per average power = $585,000,000/60,000kW = $9,750/kW.
Option 2- However, if the power is feeding into the pumped hydro plant and then into the grid, then the capital cost per average kW, for both the wind farm and the pumped hydro scheme, is: $26,250/av kW
(This is calculated as follows: 225MW capacity, 60MW average power (your figure), 80% efficiency of pumped hydro plant, 48MW average output from hydro plant. Capital cost = 225,000kW x $2,600/kW = $585 million. Capital cost per average power = $585,000,000/48,000kW = $12,187/kW this is for the wind power component only.
For the pumped hydro component we need 225MW at say $2000/kW = $675 million. This is for 48MW average power output. The cost per average kW = $675,000,000/48,000kW = $14,062/av kW. The total of the wind component and the pumped hydro component is $26,250/av kW
Storage
As I mentioned in the previous posts, the amount of storage is defined by the storage capacity of the smaller reservoir. Wind power is intermittent so we need to be able to store water in the upper reservoir so we can generate when the wind isn’t blowing. We need to store water in the lower reservoir so we can pump it up when the wind is blowing and producing more power than the grid is demanding. We need adequate storage in both reservoirs. What is adequate storage? For reliable base load power, so we will be able to pump every night, then 6 hours of storage is sufficient, although we would normally provide more. However, with wind, because of intermittency, we would need much more storage. If the system was totally dependent on this source of power we might need many tens of days of storage to carry us through long periods of low wind.
The pumps can only pump while the wind farms are producing more power than the grid demands. So we need storage. When you do the calculations for the storage required, you will find that the surface area involved is huge.
The pumps can only pump while the wind farms are producing more power than the grid demands No in my model the wind farm is not connected to the grid. It sends unregulated power (lower capital cost) through short transmission (lower capital cost) exclusively to a slightly modified hydro dam (lower capital cost). How much lower the costs could be I can’t say.
I’ll have to think this through but in some way there must be a way a valuing the fact that we have changed the wind power from intermittent to on-demand from storage. That is wind integration at the source. I believe a small scale experiment on these lines in the Canary Islands or somewhere didn’t work out or perhaps never started. If direct wind pumping is unviable it may mean that large hydros like Hoover Dam US are doomed by climate change.
John Newlands, on 11 May 2010 at 10.09 Said:
“I’ll have to think this through but in some way there must be a way a valuing the fact that we have changed the wind power from intermittent to on-demand from storage.”
The value of the wind is the value in KWhr stored as water inventory in the reservoir when it is used to generate power. The conversion from cubic-metres (or acre-feet, if you an in the US) is straight forward if you know the hydro side parameters.
John,
OK. I didn’t word that sentence you quoted properly. I do understand the scenario you are considering, which is to provide the wind power directly to storage. But the point I make is correct. When you have hydro capacity supplying the grid already it is obviously cheaper to send the intermittent wind power straight to the grid and save the stored hydro energy in the existing hydro reservoirs rather than send the wind power to a pumped hydro scheme. Your proposal makes no sense. It is about 4 times more expensive per unit of energy sent out (I used average power for the calcs above). Did you follow through the calculations I gave you?
And you still need a huge amount of storage capacity.
You say “there must be a way of valuing the fact that we have changed the wind power from intermittent to on-demand from storage”.
Yes there is. It’s called storage. It is very expensive. Pumped hydro is the cheapest. But it is still very expensive. The lack of low cost energy storage is known to be a fundamental problem for renewables. The article at the head of this thread has a figure which shows the cost of energy storage per unit of power output ($/kW) and per unit of energy storage capacity ($/kWh).
John,
Further to Storage
The area of the storage in the reservoirs is 6,300 ha (for each reservoir) assuming:
15m hydraulic head
5m depth of active storage
48MW average power generated
10 days of generation at this average power with no inflows and no pumping.
If this is a new reservoir, then the value of land area innundated at say $2000/ha = $12.6 million per reservoir, $25 million for both reservoirs.
There are differences if one takes a portfolio or system view. Imagine an integrated system with half coal, 20% each nuclear and gas, and a rapidly expanding renewable share. As more gigawatts of wind are built, keep in mind that they are ‘forced in’ by regulatory requirements, and subsidized. Also keep in mind that bidding into a power pool is done at variable or operating cost. For wind this is near zero-they are ‘must run’ to the grid and are banking on making their investment return on average over the project lifetime.
In an integrated system, if wind is showing up in low demand periods, there are only three (bad) options on offer at present: Cycle baseload units that are ill suited to cycling; pay the wind to curtail and not generate; or dump the power off on wholesale markets on the worst possible terms.
Storage gives a fourth option. Suppose the pumped storage was using both conventional and wind for pumping? Wind would be an opportunistic buy, at zero or negative cost depending on the value of ‘getting rid of it’ from the grid operator standpoint, and could be sold off at peak plus green pricing premium. To the extent that cheap off peak wind added value to the normal economics, it would make the storage scheme more profitable.
What if the portfolio tradeoff for wind integration is between building gas combustion turbines that only run 5% of the year and dumping the off-peak wind, or building pumped hydro and arbitraging the off-peak wind (along with other off-peak supply). Now which is better?
Jim of MN,
Sorry for the delay in replying. Apparently your post got held up in the moderation queue.
I’ll post some initial comments and may come back with a more considered comment later.
I agree. However, one of the policies I am trying to educate the population to reject is that we should mandate and subsidise renewable energy. I know that is the current situation, but it is one I hope we can change over the next few years. Of course we should honour all existing agreements, but I’d like us to not make any more such agreements.
I agree.
Jim, I think I understand what you are saying here, but perhaps not. I agree that if we consider only the perspective of the pumped hydro scheme, they can be more profitable if they can buyer cheaper power from wind farms, when it is available, than conventional generators. So that would make the pumped hysro scheme more profitable.
From my perspective, however, using wind power, when available, for pumping means we would be cycling the baseload power stations. The baseload power stations are already providing low cost power in the low demand periods. In Australia this is between about midnight and 6am. So if wind power is supplying intermittent power, the baseload plants have to cycle. They still have to recover their fixed costs, so they must get a higher average price for their electricity.
The last figure in the lead article for this thread helps me to explain. (Jim, I am explaining this for the other readers following the discussion). This figure shows the actual power supplied by the power stations feeding the National Energy Market on 7 August 2009. The reason the hydro is generating throughout the day is because it provides baseload power for Tasmania.
Points to notice from this figure:
1. the low demand period from roughly midnight to 6am.
2. the output from the brown coal power changes little throughout the 24 hour period. This is true baseload generation. It is cheap power. Most of the brown coal power stations are designed to run at full power and not cycle.
3. The black coal power stations are more flexible than the brown coal and these are turned down in the low demand period.
4. There is very little CCGT in the NEM yet
5. OCGT is generating throughout the day
6. Negligible contribution from wind power
The portfolio you suggested is 50% coal, 20% nuclear, 20% OCGT, 10% wind and sufficient pumped hydro storage. I’ll assume nuclear is behaving like the brown coal on this figure, so the baseload portion of your portfolio is not too dissimilar to the one in this figure.
If we had more pumped hydro the demand would be higher in the low demand period. My interpretation of your question is: What is the least cost way to supply the power during the off peak period to meet pumping demand?
It seems very clear to me that using nuclear to power the pumps will be cheaper than wind. I say this because we can’t make the investment decisions on the basis of the short run marginal cost of electricity (SRMC). We have to make the investment decision on the basis of the long run marginal cost of electricity (LRMC).
With the wind option we need:
1. Wind power (A$2600/kW)
2. Transmission for Wind (average cost A$1000.kW)
3. OCGT (A$800/kW)
4. Pumped hydro with sufficient storage for say 100 hours of peak power generation
5. Higher average cost for base load power to compensate for cycling and reduced power sold
With the no-wind option we need:
1. nuclear power (A$4000/kW)
2. pumped-hydro with sufficient storage for say 6 hours of peak power generation
It seems to me that the no-wind option would be far cheaper. But I suspect I must have mis-understood your point.
Jim, please explain again if I have misunderstood your post.
I think you did understand my point and I thank you for the thoughtful reply. Perhaps one could summarize by saying that the fact that forced/subsidized wind in sufficient quantities can make a pumped hydro scheme economic is, ipso facto, more evidence of just how much renewable requirements can distort markets.
We may differ a little on one point, in that I think the presence of a pumped hydro scheme can allow the wind to dispatch while avoiding costly baseload unit cycling, by increasing the pumping demand in tandem with the wind during off peak periods. It’s interesting to wonder, though, how much ‘slop’ there would be between the financial/contract path in which one could clear precisely vs. actual system operations where presumably the pumping could not match the wind down to the fine temporal grain of intermittancy, meaning some cycling would still take place.
I find it very interesting how much the economics of particular system assets depends on what other parts of the system are already in place. Call it a ‘first mover conditionality’. You are pointing out that it could be cheaper to run an existing pumped hydro scheme with nuclear instead of wind, while I am interesting in new pumped hydro as a storage/arbitrage/peaking solution to a surplus of off peak wind that is already ‘baked into the cake’. Different starting point, different solution. Both logically correct….I think.
Off topic but hopefully something interesting in return for your indulging my comment: In power market design there is a deep and unavoidable problem involving first movers. The existance of multiple feasible equilibrium solutions to the network optimization problem means that someone (the regulator normally) has to decide who goes first, or at least who is entered into the computer simulation modeling first. In so doing the first mover decision has a direct bearing on marginal costs (set by the last mover), and who is in and out of the money. This means that one cannot formally divorce equity considerations from efficiency considerations, as we are taught to do in microeconomics (‘first, get prices right; then figure the subsidies’).
Back on topic…If there is still appetite for this topic one other area that I wonder about is pumped hydro capacity factors: what is required for a viable project? 5%? 10%? Or higher? My understanding is that these assets do not operate many hours in the year which puts a lot of pressure on the project economics. You mention six hours per day so that’s 25%. Is that what the Australian projects operate at?
Jim in MN,
Lots of good points and good questions. I’ll have to come back to this tomorrow. I have to say, though, you are way ahead of me when it comes to the market behaviour side of all this. I leave price to others. I am stuck at cost.
A couple of quick points in answer to your post:
1. The snowymountais hydro scheme has a capacity factor of about 14%. That is excluding pumped hydro. The reason this figure is so low is because Australia is so dry. The generation is limited by the watrer inflows.
2. I don’t know the actual capacity factors for the pumped hydro. Wivenhoe is designed to pump for about 5 hours per day, generate at 7 hours per day (but not at full power) and run as spinning reserve for 12 hours per day.
3. You said
I’ll need to spend more time on this one. Because, we do differ a bit on this. I’d envisage two different types of pumped hydro schemes. One is in a system where reliable baseload power drives the pumps and the others is designed to run with intermittent renewables.
Australia’s existing pumped hydro is designed for the case with reliable baseload. It pumps each night to store energy for generating peak and shoulder power next day, and to provide rapid load follwing and grid stabiliations during the day. For this option we need only 1 day of storage. Of course we have a bit more for safety. If this system has more storage, then it can be used for emergency, and can restart the grid if there is a total system failure.
The pumped hydro system for variable power supply would have variable speed pumps. It would also need a much large storage capacity in both the upper and lower reservoirs.
More tomorrow.
Peter Lang there seems to be very little to go on with intermittent pumped hydro with just one serious project to date
http://en.wikipedia.org/wiki/El_Hierro
There’s a fun graphic in *swf of El Herro here
Given it is only covering 10MW of wind and they are using an extinct volcano to store water, it’s hard to extrapolate. That said, paying 54 million Euro for 10MW of power still sounds not too bad, all things considered. OTOH, apparently this will save them about 1.8 million Euro per year in diesel fuel, which works out at a payback time of 30 years.
There are only 10,000 people on the island so it’s not as if they have industrial scale energy needs.
Maybe one of those small nuclear “batteries” might have been better.
John,
One of the people mentioned in the acknowledgements in the lead article for this thread is currently doing some consulting work on the Iowa Hill pumped hydro project. Variable speed pump turbines are being considered for it. Google it and find out some more. David B. Benson might have some facts on it too.
Here is a lsiting of pumped hydro schemes. Somewhere I have some info on waht is happening with variable speed pump turbines and pumed hydro for intermittent renewables. The Japanese are the leaders in that field.
http://www.hydroworld.com/index/display/article-display/357777/articles/hydro-review-worldwide/volume-16/issue-6/articles/cover-story/snapshots-of-pumped-storage-projects.html
http://en.allexperts.com/e/p/pu/pumped-storage_hydroelectricity.htm
http://www.wind-watch.org/documents/cost-of-pumped-hydro-storage/
Most of those links relate to what I’d call ‘surplus baseload’ and how new dams can help. An angle that needs investigating is to what to do with chronically half full existing dams. I see them here in Tasmania and no doubt NSW and Vic have them as well. In the US there are concerns about the effect of long term drying on Lake Mead and Hoover Dam.
My cost saving idea is to use the chronically half full existing dam as the upper reservoir and elongate the outfall pond as the lower reservoir. I’d need unit costs on concrete, variable speed motors, positive displacement pumps etc to comment further.
Australia’s Pumped-Hydro Energy Storage Capacity
What is the total energy storage capacity (in GWh) of Australia’s existing Pumped-Hydro facilities?
The short answer is roughly 5 GWh can be stored per day and 20 GWh total.
Points to note:
1. The energy storage capacity is determined by:
a. The active storage capacity of the smaller reservoir
b. The minimum hydraulic head – i.e. when the upper reservoir is at its minimum operating level and the lower reservoir is at its full supply level
c. The pumping rate
d. The pumping hours per day
e. The maximum allowable drawdown rate in the reservoirs
2. Australia’s pumped-hydro storage facilities are designed to be powered by reliable, constant power, as is provided by base-load power stations. The existing pumped hydro storage facilities are not suitable as energy storage facilities for intermittent renewable energy generators.
I do not have the detailed engineering data needed to accurately calculate the energy storage capacity of the two smaller pumped hydro facilities. However, I’ll show here how I derived the total figure provided above.
Wivenhoe
Wivenhoe is Australia’s only ‘pure’ pumped hydro facility.
Power: 500 MW nominal rated power, 625 MW maximum
Average daily operating hours:
– pumping = 5 h/d
– generating: = 7 h/d
– standby and spinning reserve = 12 h/d
Energy stored per day in average pumping hours: 1,640 MWh
Total energy storage capacity in upper (smaller) reservoir: 5,171 MWh
Tumut 3
Tumut 3 is mainly a run-of-river hydro scheme with some pumping capacity. The generating capacity is 1,500 MW from six turbines. There are three pumps with a total pumping capacity of 297 m3/s.
The lower reservoir is the smaller. It would fill from empty in 6.8 hours if the Tumut 3 power station was generating at full power (1,500MW). After that time the water would spill over the spillway and could not be pumped back up. It would be lost from the energy storage system. It would take the pumps 26 hours to empty the lower reservoir (by pumping the water up to the upper reservoir).
Energy stored per day in 6 h of pumping: 2,378 MWh
Total energy storage capacity in lower (smaller) reservoir: 10,295 MWh
Kangaroo Valley and Bendeela
The rated generating capacity of Kangaroo Valley is 160MW and Bundeela is 80 MW. I do not have access to the engineering data for these two facilities so I make the assumption that the ratio of pumping capacity to generating capacity is the same as for Wivenhoe, i.e. 66%. On that basis, the energy stored per 6 hour day is: Kangaroo = 630 MWh and Bundeela = 315 MWh.
Total Energy Storage Capacity
The estimated total energy storage capacity per 6 hour day is:
– Wivenhoe = 1,968 MWh (1,640 MWh for 5h average pumping per day)
– Tumut 3 = 2,378 MWh
– Kangaroo Valley = 630 MWh
– Bundeela = 315 MWh
– Total = 5,290 MWh
The estimated total energy storage capacity of the smaller reservoir is:
– Wivenhoe = 5,171 MWh
– Tumut 3 = 10,295 MWh
– Kangaroo Valley = ?? MWh
– Bundeela = ?? MWh
– Total = 15,466 MWh + guess for 5,000 MWh = say 20 GWh
References
1. Engineering Features of the Snowy Mountains Scheme, 2nd Edition, 1982, ISBN 0 642 89182 6
2. http://www.tarongenergy.com.au/Portals/0/docs/factSheets/Factsheet%20-%20Wivenhoe%20Power%20Station%2024%20June%202008.pdf
3. http://www.sca.nsw.gov.au/dams-and-water/major-sca-dams/shoalhaven-system/hydro-electric-power-generation
I wanted to take a bit of issue with some of the assertions in the piece here. I love thorough analyses, as seems to have been done here, but there are some generalizations being made.
1. The assertion was made that pumped storage is not suitable for integrating high intermittency resources. This depends entirely on the design of the plant and the mode of operation. If you design your plant for a high storage-to-generating capacity ratio (which, admittedly, most have not been designed for so far), and select your pump-turbines to handle a wide range of input and output capability, including the use of variable speed equipment, then you can very well be suited to integrate wind and solar resources flexibly. You need to be willing to sacrifice the goal of packing it all into a peaking period and instead focus on enhancing the firm capacity of the renewable resource you’re associating with.
2. The cost figures associated with pumped storage in the literature do not match the figures associated with projects currently under development in the U.S., nor many of those recently in Europe. The figure of $800/kW is probably low, but they need not be $2,000 either. There is a very wide range of costs, very much dependent on the amount of civil engineering required, lengths of tunnels, steel lining (as mentioned by others), environmental mitigation, etc. For example, closed-loop projects using natural landforms, high-head, short distance between upper and lower reservoirs, being close to transmission, good geology, etc. will contribute to significantly lower costs,
I’ve always advocated for smaller, eco-friendly, efficient storage projects designed to support renewables.
Matthew Shapiro,
Thank you for your comments.
A high storage-to-generating capacity ratio means a large area must be inundated in both the upper and lower reservoirs. If the storage to generating ratio is high, then we need a vast area inundated for little power.
Compare the surface area of storage required for a high and a low-storage to generating capacity ratio, with all else equal. With pumped-hydro acting as a peaking plant matched to a base-load plants then we might need say 5 or 6 hours of storage per unit of power (eg 1 GW power and 6 hours storage = 6 GWh). This is because it can be refilled every day, with certainty, from the power supplied by the reliable base load plants. The area of the reservoirs is 6 units of area.
However, if we want 1GW of power for 6 hours each day from our pumped hydro plant and it is to be filled by wind power, then we would need perhaps 100 units of area for the storage. This is because we’d need 100 hours of storage (100GWh) or more because of the days when the wind doesn’t blow. (By the way, this has been the case for about 4 days from 17 May to 20 May over the whole NEM and it is still continuing).
We’d also need:
– 3 GW of wind power capacity based on annual average wind conditions or much more than this based on the average over shorter periods. The amount of capacity is determined by the amount of storage available.
– Transmission capacity from every wind farm to enable the full capacity of the wind farm to be transmitted when the wind farms are generating full power.
– Pump capacity able to utilise most of the full power supplied by the wind farms on the few occasions when it is available. (I’m exaggerating to make the point clear for all readers, but only a little).
– Optimise the size of the pumps, wind farm capacity and storage capacity. However, this will cause substantial losses. Perhaps only 25% or so of the actual wind farm’s energy output can be captured. Most of the remainder must be spilled.
– I recognise that we can bury the problem by assuming the other generators on the grid can be cycled to shadow for the wind power. However, whichever way you look at it, using pumped storage sites for storing excess energy from intermittent renewables is an expensive and inefficient way to use our few available pumped storage sites.
Which US and European projects are you referring to and what are the costs. Can you provide links to authoritative sources? I agree with your statement that there are a very wide range of costs and they are dependent on the factors you describe. The ideal features that would give us lower costs are not available in Australia. The costs for the Tantangara-Blowering project are very rough. However, they are more likely to be higher than lower. I’ve done some more analysis on it and it is looking more like $10 to $15 billion for 8 GW power and about 40 GWh per day storage capacity. I expect other constraints on the upper reservoir would limit the total storage capacity that could be used for pumped hydro storage to perhaps 100 GWh, but I have not investigated this. I have not analysed the project from the perspective of variable speed pump turbines because I suspect it would be totally uneconomic for the reason outlined in Point 1 above.
I hope your advocacy remains rational and based on sound engineering analysis. Unfortunately, rationality is not considered important by many of the overly enthusiastic renewable energy advocates.
Matthew, Shapiro
Here is another way to compare the value of pumped hydro storage for different uses; either designed for use with baseload source of power or intermittent, unscheduled source of power.
The Tantangara-Blowering pumped hydro site could provide 8GW of peak power every day for 60+ years if it is designed to be paired with base-load power sources, such as nuclear. If paired with 25 GW of nuclear plant the nuclear + hydro could meet all the NEM’s current electricity demand, including the peak demand.
However, if Tantangara-Blowering was designed to be energy storage for intermittent renewable energy, such as wind power, it could support 1.6 GW of wind capacity for just 4 days of little wind.
We have experienced just such a low wind situation in the NEM during the past week. The wind farms in the NEM are dispersed over a distance of about 1100 km. The NEM is the world’s largest electricity grid in aerial extent (so I am told). Despite this, the 1.6 GW of installed capacity has delivered just 10 MW average power for 4 days. That compares with 480 MW expected if we assume 30% average capacity factor. So we are deficient by 470MW for 96 hours (it’s actually much longer than that). We would need 45 GWh of storage in our pumped hydro scheme to have provided the power while the wind farms were on vacation. So our $15 billion Tantangara-Blowering pumped hydro scheme couldn’t make 1.6 GW of wind power capacity supply even 0.5 GW of reliable reliable base-load power supply, let alone 25 GW.
This must surely make it clear that using pumped hydro sites as energy storage for intermittent renewables would be a totally irresponsible waste of our assets. Consider how the future generations would consider such irresponsible actions by us!!
I should correct an error in my previous post, before I get caught out. The actual output and the capacity factor of the wind farms in the NEM, total capacity 1609MW, for past 6 days were:
Date MW CF
17/05/2010 31 1.9%
18/05/2010 19 1.2%
19/05/2010 51 3.1%
20/05/2010 80 5.0%
21/05/2010 168 10.4%
22/05/2010 242 15.0%
This correction would have an insignificant effect on the statements in the previous post.
Peter, BZE has 40% of demand being met by 2020 in their new storyline. This is an average power of roughly 10 GWe, based on around 30 GWe peak (I need to check their exact figures, but this is about the gist of it). On this basis, if PH was used to ‘make up the difference’ between their expectation and reality, how much stored energy would need to have been drawn upon over that 6 day period you cite? I make it as a ~1,200 GWh deficit over 6 days.
Barry Brook, on 24 May 2010 at 12.08 Said:
Below are some extracts from the BZE “Zero Carbon Australia by 2020” Executive Summary http://media.beyondzeroemissions.org/preview-exec-sum14.pdf
From my reading of the BZE “Zero Carbon Australia by 2020” Executive Summary, the authors are not proposing any more pumped hydro storage capacity. They are relying on the energy storage at the CST power stations and some biomass for back up.
However, let’s consider the question you have asked on the assumption that pumped hydro has to ‘make up the difference’ between their expectation and reality. The existing pumped hydro storage capacity is about 20GWh. This would back up for the deficient wind power for about 1.3 hours only. If we wanted pumped hydro capacity to back up for the wind, to ensure we had at least 30% of the wind power’s capacity supplied at all times, I calculate we would have needed 1,728 GWh of storage for these 6 days.
Basis of Estimate:
Average actual capacity factor for 6 days = 6%
BZE assumed average capacity factor = 30%
Capacity factor deficiency = 24%
BZE Capacity of Wind power = 49.5GW (say 50GW)
Energy deficiency = 24% x 50GW x 24h x 6d = 1,728 GWh
That is about 85 times our existing pumped hydro energy storage capacity. And this is for just 6 days. For 6 months of below average generation from wind power, I could envisage us needing 1000 times our current pumped hydro energy storage capacity.
I reitterate, however, that BZE analysis does not assume adding any more pumped hydro energy storage capacity.
Thanks Peter, that’s similar to the 1,200 GWh I estimated in the post before yours — my estimate is lower because I used a figure of 30 GWe of installed wind instead of 48 GWe. Scaling mine up, i.e. 48/30 * 1,200 = 1920 GWh, which is a little more than your figure, but I did it on daily averages rather than the overall 6-day average CF.
Peter:
On the cost estimates, first the U.S. projects: the published documents associated with the permitting of several U.S. projects with the FERC indicate costs of $970/kW for one (Eagle Mountain) – which uses mine pits for reservoirs, and Lake Elsinore Advanced Pumped Storage (LEAPS) – at about $1450/kW; neither include transmission. For European projects and projects in Asia, you need to hunt around for cost figures on a project-by-project basis, as I have, and there’s also the September, 2009 article from University College Cork (Ireland) titled “Techno-Economic Review of Pumped Hydro Energy Storage Plants” (available online) that shows the range of figures for mostly European projects. Also, the figures published for the newest South African projects both come in at well under $1,000/kW. Part of it certainly must be related to the cost of doing business in a given country (e.g., Japanese projects tend to be on the expensive side).
Regards,
Matthew
If it’s any interest here is my neighbour’s newly connected microhydro. Head 21m through 30cm pipe. Average turbine speed 1500 rpm connected to an asynchronous 230v three phase generator. Max output 14 kwe. Metering is 26.5c per kwh which was the pre-existing tariff at the adjoining farmhouse. There is no special feed in tariff or credit for RECs.
The turbine room a stone hut.
————————
Water exits below the hut.
The owner is under no illusions it makes any difference at all. It just suits his property.
John,
Thank you for this. I love these micro hydro hydro schemes, but for interest not for economic reasons. I had a small part to ply in a very similar scheme in Canada, From memory it was about 80kW and it generated that power all year. When the power generated was excess to demand (it was off grid), the excess power heated water in the tailrace.
The really valuable pieces of information you could give us, if your friend will release them, are:
1. The total cost of the system (all costs inlcluded)
2. Energy generated per year from the 14kW plant
Matthew Shapiro,
Thank you for the cost info for some pumped storage sites.
Australia is not average with hydro or pumped hydro because we have relative low topographic relief and less water when compared with USA, Europe and Japan.
Here is a list of some recent pumped-hydro schemes including costs.
http://www.hydroworld.com/index/display/article-display/357777/articles/hydro-review-worldwide/volume-16/issue-6/articles/cover-story/snapshots-of-pumped-storage-projects.html
What I find interesting about the figures above is that even if one were to use the least cost figures above ($970 per Kwh, as opposed to the $2000 Peter Lang has used) is that the six days of coverage would have implied a spend well in excess of $1.5 trillion dollars, even assuming the capaicty to build and connect at that cost were available.
Then of course you have an empty reservoir, which is utterly useless until enough surplus wind (or fossil fuels) is used to replenish it. You actually have to do that pretty quickly otherwise you have no spare capacity at all if there’s even a brief dip in wiond capacity.
Realistically you’d be switching your fossil fuel sources on well before you got near exhaustion of the pumped storage and since it was such a substantial task you’d probably choose your cheapest source — in this case coal, probably brown coal.
So at the end of the day you have a lot of expensive wind, a hideously large and expensive pumped storage capacity standing by for wind you expect to be no use and finally you have to have fossil fuels in at worst black start readiness anyway.
Yet if you just went with a purely CCGT-based system you could just use the existing pumped storage to manage slews and run the CCGT at optimal efficiency and have no major outlays outside of the new gas capacity. Total CO2 abated per dollar of outlay would be far smaller and if you really did want to spend more you could cut deeper into emissions without the wind for still a fraction of the price.
Ewen,
I agree with the point you are making but you are confusing the unit cost of power (kW) and unit cost of energy (kWh). Have a look at the chart in the lead article (the one full of coloured rectangles just before the Conclusions). The chart plots Capital Cost Per Unit Energy versus Capital Cost Per Unit Power. Capital Cost per unit energy fror Pumped hydro is around $50 – $150/kWh. Note the log scale on both axes.
Ewen,
I calculate a rough cost for sufficient pumped hydro storage capacity to allow wind power to meet the NEM’s demand for power at all times as follows:
1,728 GWh (from above) for sufficient storage for the 6 days 17 to 22 May 2010
= 1,728,000,000 kWh
@$100/kWh for storage capacity (ref. figure in lead article)
= $172.8 billion
How much storage capacity would we need for 6 months of low wind conditions for an average year? Say 10 times this amount? And how much for a worst case, low wind period? Say 20 times?
Estimated cost for sufficient pumped hydro energy storage capacity to last through a worst case low wind year:
= $172.8 billion x 20
= $3,460 billion
No problem! Put it on credit? Worry about it tomorrow! Let the next generation worry about it! And all future generations !! 🙂
Look at it on an annual average basis. Taking a purist point of view on who’s using the storage facility is not helpful; rather, attempt to work the ratios between wind capacity, storage generating and pumping capacity, and storage volume such that you minimize the need for the latter to maintain a given amount of supply to the grid. You won’t be getting 100% of your charging energy from wind. Throughout the year, there will be times when much of it is coming from wind, and you are firming wind with wind. At other times, you will be using more off-peak baseload resource to maintain the required reserves. The end goal is to maximize the amount of non-polluting, flexible supply in the system while maintaining reliability at the lowest cost. Wind and solar can be part of that.
Peter Lang re microhydro economics; the owner claims it cost around $40k as a result of using second hand hardware and mates to do the trade work, though fully certified. Since this years rainfall is nothing like last year it will be tuned to earn around $250 pw giving a payback period of about 4 years. Tuning involves setting the nozzles to produce a target output with the least water flow, say
40 L/s (flow) X 20m (head) X 9.8 ( g) X 0.7 (efficiency)
= 5.5 kw
It will only produce 14 kw if the big rains come like last year. The annual average output will probably be in the range 5-10 kw X 8,760 h = 44 – 88 Mwh.
Thank you John. For an analysis to be of much value we’d need to do the calculations on the basis of the commercial cost of such a system. We’d also need to have a cost for operation and maintenance. You’ve just mentioned it needs an operator to tune the nozzles from time to time. I wonder what the true operation and maintenance cost would be on a fully commercial basis.
Matthew Shapiro,
@ 2 June 2010 at 0.18
I strongly disagree with your approach. What you are proposing is what the RE advocates attempt to do all the time. That is to muddy the waters so much that no one can see the reality.
Do not use averages. They hide the reality. We need to be able to provide power that is demanded at every point in time.
If you follow through the analysis in the lead article, in the comments, and on the other threads I and others have posted on BNC, you can see that the cost of storage for renewables is exceedingly high.
You need to separate out the components to understand the cost. Otherwise you fall into the trap of burying the true costs of renewables in a system such that the true extra cost caused by renewable energy is not visible.
Matthew,
Are you genuinely interested in finding a viable solution, or are you more interested in trying to promote a belief in renewable energy?
If you are genuinely interested in finding viable solutions to address a problem, can I suggest you define the problem then dispesne with the adjectives. Crunch the numbers and estimate the cost of your proposals. Then we can have a serious discusion. Otherwise we are simply discussing a belief – “renewable energy is good because it is good”.
I’m simply an advocate of living in a manner that leaves as little trace of damage in the long run as possible. Any long-term thinker will consider renewables seriously, even if they are more expensive at the moment.
As for averages, demand at any given moment is based on averages. Even conventional plant outputs have “average” reliabilities of a given number, and can be forced out unpredictably. Wind happens to be quite variable – but it is okay to use averages for it, too, so long as we have a means (the storage system) that helps fit the overall energy flow with the demand at a given point in time.
For for illustration’s sake, a 200 MW storage plant, with a reasonable amount of storage, coupled with a 300 or 400 MW wind plant can – over the long term – operate as an integrated entity with firm output; one that can (under circumstances of a good wind resource and a well-chose storage site) compete directly against conventional sources. So the addition of storage is incremental, not on a par. You don’t need to add the cost of wind/MW plus a MW of storage (that would indeed be expensive). And different types of sites or wind patterns and demand patterns will require different types of configurations. And as I mentioned previously, there is a role for other baseload sources to play in there as well. Even with half or so of the charging energy used to maintain the reserve coming from a non-wind source, you still end up with a product that is mostly renewable in nature.
Now, as I tried to point out, in extended wind lull periods, the lion’s share of charging energy will come from off-peak baseload sources; in extended high wind periods, the lion’s share of charging energy will come from wind. That is okay, and that is why using averages is okay. You just need to look ahead at the seasonal and diurnal patterns based on historical information to determine where it’s safest to set your basic thresholds of firm capacity commitment for the integrated product.
Matthew,
I’m simply an advocate of living in a manner that leaves as little trace of damage in the long run as possible. Any long-term thinker will consider renewables seriously, even if they are more expensive at the moment.
What you either don’t realise or are ignoring is that “renewables” are not renewable. Only the fuel is renewable. Renewables require 10 times more concrete, 15 times more steel, and tens of times more of other non-renewable material. So they require far more mining, far more area disturbed for mining, and far more area for the actual plants. Renewables are not as sustainable as nuclear energy, not even close. So the reason you should look more closely into your belief is not just about cost. Renewables are less sustainable than nuclear. There are several other threads on the BNC web site where this has been covered and discussed at length in the comments.
Matthew,
What you either don’t realise or are ignoring is that “renewables” are not renewable. Only the fuel is renewable. Renewables require 10 times more concrete, 15 times more steel, and tens of times more of other non-renewable material. So they require far more mining, far more area disturbed for mining, and far more area for the actual plants. Renewables are not as sustainable as nuclear energy, not even close. So the reason you should look more closely into your belief is not just about cost. Renewables are less sustainable than nuclear. There are several other threads on the BNC web site where this has been covered and discussed at length in the comments.
Matthew,
We can’t even begin to sidsucc something like your example when you make statements like this:
I retort: most pumped storage sites have a few hours of storage at full power. So what on earth oare we talking about? The whole post is so loaded with adjectives we can’r discuss it in any meaningful way. Could I urge you to consider the pdf paper linked from here:
http://bravenewclimate.com/2009/08/16/solar-power-realities-supply-demand-storage-and-costs/
Even though this article is about solar and pumped hydro storage, it will give you the gist of what is required for pumped hydro to provide sufficent storage to make intermittent renewables viable. Note the costs. The discussion in the comments covers many of the points you are making.
@Mathew …
I agree completely. I share your desire to leave a small footprint and spent most of the first part of my life as an adult considering renewables seriously, even though I knew they would be more expensive. I put a significant value on treading lightly.
What I found though was that I’d grossly underestimated just how much more expensive RE would be in practice. When I began investigating I discovered that others who had considered renewables seriously and had solid expertise in the field found that they simply couldn’t do the most important job most RE advocates, me included, wanted them to do — the job now being done with fossil fuels, except at an unrealistic premium and maybe not even then. It suddenly became very clear why what had seemed obvious to me — renewables were the way to go — was being ignored by almost everyone with the dollars to invest. They weren’t stupid or ignorant or greedy (well they were but that was beside the point). They simply could not see any way they could break turn a profit on the deal, even with a state subsidy. Sad but true. After all, if you could sell “clean energy” for only a modest premium on coal or gas (and thus for the same price with a modest subsidy), why would you not do so? A dollar is a dollar, however you get it.
I also found out that nuclear power was a lot less polluting and dangerous than I’d thought. As Peter points out, it involves a far smaller footprint in practice than renewables.
The problem is the numbers. If you are going to supply an industrial scale energy system you must have despatchable output i.e you must be able to promise to deliver exactly so much power to the grid at a given moment in time. If you can’t do that what you can produce at random times is simply not commercially useful.
The point Peter makes is that it is not the average output of windfarms that is key. It is the minimum output that is critical in assessing storage needs. If there are times when you are only producing 5% of what you could produce at best or of what you would produce on average then one of these has to be the benchmark for your storage or your fossil fuel cover. It you expect, for example, on on average to supply the grid with 400MW then you must have the shortfall from 400MW at any given time in storage perpetually or a fully despatchable source able to fill the gap on the same notice you have of the shortfall. Either solution is very expensive unless the average and the minimum are very similar. They aren’t , so “reasonable storage” doesn’t cover it. The question is how far into deficit will you go before your average power output recovers to that you predicted? Nobody can say that with certainty. It is politically unacceptable for any government to load shed in circumstances where they ought to have been able to avoid it and so no government will take that risk.
As Peter demonstrates in the Hazelwood thread, trying to use wind with gas shadowing costs a lot but at the margin, doesn’t produce significant reductions either in emissions of reductions in fossil fuel usage and yet it is very expensive.
[…] Hydro Power Storage is quite expensive with estimates ranging from $500-$1500/KwH which is comparable to the most expensive forms of Energy Storage like Lithium Batteries.This form of Energy Storage also leads to losses of between 15 – 30%.There are also minor problems of environmental impact of large hydro plants and availability of favorable sites. The main advantages are that it uses existing infrastructure of Hydro Power which has a large global installed base.In the 1930s technology was developed for building Turbines which could generate Electricity and also serve as Motors allowing Storage of Hydro Power.Also Pumped Hydro Storage has High Reliability of >99% and relatively Long Cycle times which means that the stored electricity can be used in a few hours to a few days. […]
There is an important error in the previous post. It highlights the frequent confusion between power, energy, and energy storage capacity.
This should be restated as follows:
Hydro Power Storage is the cheapest electrcity storage technology with estimates ranging from $500-$1500/kW power and $50-$150/kWh energy storage capacity which is about 1/10th the cost of forms of energy storage like Lithium Batteries
[…] has 2.5 GW of pumped hydro. 1.5 GW of that is the Tumut 3 system which can generate full power for 6 hours. Then it requires 21 hours to pump it back up […]
Neil Howes @ http://bravenewclimate.com/2010/07/14/zca2020/#comment-85915
Tantangara Reservoir is a component of the Snowy Mountains Hydro Electric Scheme. Its purpose in the scheme is to divert water from the upper catchment of the Murrumbidgee River to Eucumbene Reservoir for long term storage. Eucumbene Reservoir is the large central storage reservoir for the Snowy Mountains Scheme.
Tanatangara operates between empty and full. Seasonal waters flow into the reservoir and are diverted to Ecumbene Reservoir as fast as the tunnel can move the water. Sometimes Tantangara Reservoir fills faster then the water can be diverted. When this happens Tantangara Dam overflows and water is discharged down the Murrumbidgee River. This water is lost from use for hydro electricity generation. It generates no electricity. So overflowing is a loss of potential stored hydro energy.
If we were to use Tantangara Reservoir for pumped hydro, then the proportion of the reservoir’s volume we use for pumped hydro storage is storage removed from use for Tantangara’s intended purpose. If we wanted to use all of Tantangara Reservoir for pumped hydro storage in the way envisaged by Neil Howes – that is, using 526GWh of potential storage to back up for intermittent wind power – then Tantangara Reservoir would need to be kept full throughout the year so it is ready to generate at high power for days at a time. To do that would mean Tantangara Reservoir could not do its job of capturing the seasonal inflows from the upper Murrumbidgee River and diverting them to the central storage (Eucumbene Reservoir) for future use in generating electricity. So the capacity factor of the Snowy Mountains Hydro Electric scheme would be reduced forever. It would produce less hydro electricity forever more.
The Tantangara-Blowering pumped hydro scheme I envisage is a traditional pumped hydro plant that would pump the water up every night at the times of least demand on the grid. At this time power is cheap and is supplied by the least cost baseload power stations. I envisage these being nuclear power stations in the future. If we used Tantangara-Blowering as I envisage we would use only up to about 40GWh of storage. That would amount to less than 10% of the total storage of Tantangara. So we would effectively lose only 10% of Tantangara’s capacity to capture water for traditional hydro electric generation in the years when Tantangara overflows.
If Tantangara-Blowering is developed as a traditional pumped hydro scheme for use with low cost baseload power in the early ours of the morning it can provide 8GW or peak power (high value power) every day for 80 odd years. That would avoid the equivalent of eight nuclear power stations. It would cost about $15 billion and save about $32 billion in nuclear power stations (the nuclear power stations to do the same job, in a fossil fuel free world, would be load following and used at a capacity factor of about 20%). That is the really great value of pumped hydro if we do not waste it on propping up renewable energy.
However, if the site was used for supporting wind, we’d need to use all Tantangara’s capacity for pumped hydro and would lose its use for conventional hydro. Tantangara Reservoir would need to be kept full so it is able to provide essential power in the infrequent events where the wind isn’t blowing and there is insufficient energy stored in the molten salt at the solar power stations. This would be an enormously expensive way to ensure a secure supply of electricity. It is totally ludicrous suggestion when you really think about it. The $15 billion investment would be for a plant that is required rarely but then is essential to keep our electricity system running.
It would be irrational to use our limited hydro resources and any other potential sites for the purpose of supporting wind power.
I’ve answered the other points in your post before on this thread and several others.
Neil Howes, your advocacy of wind power is irrational.
Compare the cost of wind power and nuclear power on the basis that they must be able to provide baseload power:
Requirements:
Power is available whenever we demand it – every instant of every day and all through the night.
Cost of nuclear power
Assumptions:
1. the first nuclear power station would cost the same or less than the first nuclear power station to be built in United Arab Republic (contract for four APR1400 units awarded to a Korean consortium a few months ago); i.e.
A$4,100/kW
2. The cost of further units would decrease over time, to say
$3,000/kW for the sixth unit.
Cost of wind power (to provide reliable, on demand power)
$2,600/kW for the Wind farms.
$1,000/kW cost for transmission and grid enhancements to manage the peak and fluctuating wind power
$1,000/kW for gas generators to provide the power when the wind is not blowing at full power
$4,600/kW total
But wind power delivers, on average, only about 1/3 the energy of a nuclear power station of the same capacity. So we need 3 wind farms to produce the same energy per year (or average power) as a nuclear power station. So the cost of the wind farms to provide the same energy as a nuclear power station would be:
$7,800/kWy/y of average power for the wind farms
$3,000/kWy/y of average power for the transmission and grid upgrades
$1,000/kWy/y for gas generation for backup when there is no wind
$11,800/kWy/y total
An alternative to back-up with gas generators is to use energy storage, such as pumped hydro, compressed air or batteries. Pumped hydro is the cheapest option where the appropriate topographic and geological conditions are available (Australia does not have much economic hydro potential near our major demand centres).
If we did have economic pumped hydro sites available the cost might be something like this:
$7,800/kWy/y of average power for the wind farms
$3,000/kWy/y of average power for the transmission and grid upgrades
$1,500/kWy/y for pumped hydro generating capacity
$100/kWh for energy storage capacity and we’d need say 50 days energy storage to get us through the low wind season; 50d x 24h/d = 1200h x 1kW @ $100/kWh =
$120,000/kWy/y of average power
$132,300/kWy/y total (cost per kW average power)
Peter Lang,
Neil Howes, your advocacy of wind power is irrational.
Possibly the way you are advocating that pumped hydro would be used to support wind and solar power is irrational. I was pointing out that you stated only 40GWh of pumped hydro was available in the Tantangara/Blowering scheme when you had earlier stated 525 Gwh “potential”. I was not proposing that Tantangara be kept full. By linking Tantangara, Eucumbene and Blowering with a least one tunnel each, about 600,000ML of the 1,600,000ML active storage could be used (1200GWh) without compromising long term storage.In fact it could ensure no water was lost from Tantangara as all would end up in Blowering or Eucumbene. During each high wind event( <48h) in SE Australia, up to 8GW surplus wind power would be used
to pump (4,000ML/h) or 200GWh storage( 18% of working pumped storage), and save up to 700GWh of CSP thermal storage. As well no hydro would be used for peak demand( saving 80GWh/2days). During lower wind periods( in SE) some of the thermal storage would be used, and most of the 200GWh pumped hydro used saving additional hydro and some CSP and wind from outside the SE would be imported(up to 8GW).
During really low wind events in SE( generally <24h but sometimes up to 120h) 8GW of long term pumped hydro, 5GW( 2.3GW in Snowy, 2.2GW in TAS) would be used generally for <24h but for about 12-24 days per year in total. Running Snowy at 10.3GW for even 5 days is only going to use <1300GWh storage, with <10% lost via Murray. TAS hydro would be using 280GWh (<2weeks average consumption and 2% of storage). After the first 24h of low wind or when CSP storage was low could start up existing 4GW NG fired power(mainly May to July), generating another 380GWh in 4days, but at a very low annual capacity factor or using NG to top up CSP storage.
Longer seasonal balancing could be mainly achieved by adjusting TAS hydro storage(at a maximum rate of 25-50GWh/day or 6,000GWh over 3-6 months.), with no annual change to storage except in very wet years when more hydro would be used.
At a time when we need an energy common denominator, pumped storage of water may be efficient on site if the conditions are right, but pumped storage of water, as opposed to compressed air, can’t be portable.
I believe in wind to compressed air to the pipes, as a portable energy solution. The compressed air can easily be produced offshore, as dragging air down to depth compresses it. The beauty of the compressed air is that it can be used with any fossil fuel. The new compressed air vehicles that also use gasoline are efficient.
check out the Tripe System Report on http://www.environmentalfisherman.com It is a system converting wind to compressed air, wind to Hydrogen, and wind to ORCA, or oxygen rich compressed air. Steven J. Scannell
If you google, the FortisBC Resource Plan you will get the detail of a $510M pumped hydro plan for Nicola lake.
The project has an maximum output 770 MW of 2250 floding 25 ha max 8 hectare min, and will pump a huge recreational water body up and down 6 inches every day with associated massive methane emissions. There is zero chance the enviro’s will let this one through. Maybe if they used sea water they might have a chance.
With full utilization the project would output 2250 GWH annual into the grid in peak hours after sucking 3000 GWH into its pumps at night – 75% efficiency.
If we only look at the power input as if it was a power plant the cost per GW avg is $2B/Gw (.510/(2250/(365*24)))
By comparison the last Candu 6 build in at Qinshan was $2B a GW and somewhat less than the $2.5B/Gw currently quoted for first of kind Candu ACR-1000 builds in Canada.
http://www.cnnc.com.cn/tabid/168/Default.aspx
It is more than the current and twice the predicted cost for mass produced nuclear power based on the massive builds of American designed nukes built by American engineers in China today.
http://nextbigfuture.com/2010/08/china-leverages-learning-curve-cost.html
We can build better airplanes cheaper than the Chinese in the most highly regulated industry on earth. We should be able to compete on nukes after America’s major cost and delay factor the NRC is upgraded to an OECD standard regulator like Canada’s CNRC. We invented the damn things nukes after all.
So like at lot of things stupid greenie attorney politicians come up with the idea is idiocy. Better to build the nukes and use them off peak for off peak power would be used for hydrogen/methane fuel production, COGEN, desalinization, heat storage and cooling ice storage and charging of electric vehicles.
Seth,
Thank you for that info. It is really interesting for several reasons. It shows:
1. It is the same cost per kW as a CANDU6 nuclear power plant.
2. It generates 38% the energy of a CANDU6 per year
3. So electricity would be, roughly, 2.5 times the cost of energy from a CANDU6 (Both have O&M costs but nuclear would be a little higher)
4. It generates for about 8 hours per day (during day time and evening peak)
5. It sucks power from the grid that is generated by coal power stations for about 12 hours per day (during the night).
6. Because of the 75% efficiency, the electricity generated i, in effect, emitting 133% of the normal emissions from a coal fired power station.
7. The 770MW pumped hydro plant, if paired with three CANDU6 plants, would provide peak power up to 33% above the baseload and allow the CANDU6′s to run at full power full time (apart from during mainenance). That happens to be exactly the ratio we have in the NEM (in 2007). Our baseload was 25GW, minimum was 17 to 20GW depending on the season, and peak was 33GW.
8. This would allow three CANDU6 units to run at full power, full time, and thus at least cost. This would be the ideal situation.
9. Also note, that wind power could not provide the power for pumping because wind power is not reliable and not cheap.
Point to note: BC has some of the best hydro and pumped hydro potential of anywhere in the world. Yet even in BC, the cost is $2/W.
Thanks again Seth, really interesting. Consistent with everything we’ve been saying in this thread and others.
Very interesting discussion !
The concept to build a pumped-hydro facility by connecting two existing reservoir with a tunnel and with a cavern power plant is applicated in Europe for several pumped storage projects recently.
For instance, projects in realisation:
– Nant De Drance, Switzerland, first step 600 MW, final 1000 MW
– Vianden 11, Luxembourg, 120 MW
Project under investigation:
Lago Bianco, Switzerland, 1000 MW
[…] Because wind is so fitful, and because power providers have to supply load on demand, back-up generators are required to fill in the gaps when the wind gusts or fails. Hydro power is best for this, but in Australia that resource is already fully utilised, so any new windfarm capacity will require the building of additional generators. In practice the solution is to add a gas turbine generator of the same capacity as the windfarm. This back-up must be running at all times so that wind fluctuations can immediately be compensated, otherwise blackouts will occur. The costs of construction of the back-up generator should be counted when assessing the capital cost of the windfarm. The running costs and carbon generation of the back-up should be counted when assessing the cost of power and the carbon emissions of the windfarm. For a rough cost comparison see this comment: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-86108 […]
Dear Mr Peter Lang would you be so kind to give your opinion about this method show on google :
CASCADING MARINE HYDRO ELECTRICAL GENERATION APPLICATION OCEAN .
since you are an expert Eng in this HYDRO field we would like to have your opinion in this specific field
thanks
Tantangara-Blowering Pumped Hydro – suitability for energy storage for renewable energy generators
The Tantangara-Blowering pumped hydro project would not be suitable for energy storage for intermittent renewable energy generation.
First, to be viable, the sell price of electricity from the pumped hydro scheme needs to be about four times the buy price – so the electricity needs to be generated by low-cost, baseload power stations.
Second, the pumped hydro scheme needs to generate for around 8 to 12 hours every day to earn enough revenue to pay for the capital cost. So it needs a reliable, constant supply of power for about 6 to 8 hours every night when demand is low and electricity is cheap. Intermittent generation throughout the year would not earn enough revenue to pay for the plant. (see Reviewer 1’s comments in the article at the top of this thread).
Third, it is not possible to frequently reverse the direction of the water flow in the tunnels, as would be required if used to store energy from intermittent renewable generators. The tunnels contain 20 million tonnes of water. The flow rate at full power is 3 m/s. Consider the power required to stop 20 million tonnes of water flowing at 3 m/s and pump it back in the opposite direction.
Fourth, for intermittent renewables we’d need much greater storage capacity. The storage required for 5 hours of generation at full power (8 GW) is 40 GWh. That is what is needed to allow the pumped hydro to pump every night and generate every day at peak times for the life of the project. Contrast this with the situation if we wanted to use intermittent renewable energy generators instead of reliable baseload generators. The plant would need enormous storage to allow it to generate during long periods when the renewable energy plants are generating insufficient power. We’d need sufficient storage to cover for days, months and decades of below average generation.
Fifth, we cannot use the full storage capacity of Tantangara Reservoir for pumped hydro. Tantangara’s main purpose is to capture spring run off and divert it to Eucumbene Reservoir for long term water storage (to ensure water for hydro and irrigation during decade-long droughts). I suggested using about 0.6m height of Tantangara’s water (at full supply level, more at lower levels) for pumped hydro storage. This gives 40 GWh of energy storage. The other water in the reservoir could be used for emergency if required and when Tantangara is full the scheme could generate up to 500 GWh, in an emergency situation.
The proposed Tantangara-Blowering pumped hydro scheme is unsuited to intermittent renewables.
Peter a possible solution to the flow reversal problem is to have separate water circuits. Rather than reversible motor-generators that need to be built into the hillside merely keep the existing generators (if they have spare capacity) and build a separate water lifting system as an add-on. How the cost compares I don’t know but it wouldn’t require tunnelling or much concrete.
With climate change some once mighty dams may be chronically low (e.g. Hoover Dam USA) therefore they could generate more power with their existing turbines with increased water flow. Assuming there is a cheap enough external power source some of the outlet water could simply pumped back up to the lake with the dedicated pump. If that pumping is irregular the large volume of existing water smooths out the fluctuations.
As you say logically this suits excess baseload. I believe many people now have a psychological need for wind and solar so this could help give them the reassurance they need.
“I understand manyufacturers are working at the moment to double them up.”
In Nestil, Switzerland, VA Tech Hydro have installed a Francis machine with 4 runners in series. They can deliver over 1000 m head. The quadro-runner unit is primed with a Pelton machine.
Dirk,
Thank you for that information. Can you provide a link?
Is that 1000 m head being used for pumped hydro or just hydro?
What is the maximum power output per generator?
The concept in the lead article is for 923 m static head and maximum total generating capacity of 9,018 MW (at maximum static head). If we assume twelve turbine-generator-pump sets, the maximum power output per generator is 750 MW.
So, the Tantangara-Blowering Pumped Hydro concept needs reversible Francis turbines for pumping and generating, with maximum static head of 923 m, and suited for generating 750 MW power output. Is the state of the art here yet? If not, how long until we get there?
By the way, I suspect there would be no need for such a scheme until well into the 2030′s. It would not be viable until at least 50% of our baseload power is being produced by nuclear power.
Goldisthal Pumped-Storage Plant: More than Power Production
http://www.hydroworld.com/index/display/article-display/351208/articles/hydro-review-worldwide/volume-15/issue-1/articles/goldisthal-pumped-storage-plant-more-than-power-production.html
Some points of interest:
1. The time it takes for large capital projects like hydro to go from initial concept to completion. This one started in 1965 and was competed in 2004. That is 40 years.
2. The story of the interrupted progress through investigation, delays, deferments, financial and political interference is common. It’s worst with nuclear, but happens with all technologies.
3. The information about the variable speed turbines is interesting. They are used for controlling fluctuations in grid power. This is definitely not a plant designed for or useable with the variable power output from intermittent renewable energy generators like solar and wind power.
This link is interesting and contains the key engineering features on the last page. http://www.andritz.com/hydro-media-media-center-large-hydro-goldisthal_en.pdf I’ve compared some key figures for Goldisthal and Tantangara-Blowering. These highlight what a huge scheme Tantangara-Blowering would be by today’s standards. The Goldisthal plant is tiny in every respect in comparison
Goldisthal versus Tantantangara-Blowering
head (maximum static) m 325 924
Maximum power output MW 1,060 9,018
Max power per generator MW 265 750
Flow rate
– generating m3/s 412 1,133
– pumping m3/s 320 595
Storage m3 12,000,000 238,800,000
Headrace tunnels
– number 2 3
– length m 825 53,000
– diameter m 6.2 12.7
Here is the table with columns separated by semicolons. Copy to Excel and pars with “:” to display in columns.
Goldisthal versus Tantantangara-Blowering;
item;units;Goldisthal;Tantangara-Blowering
head (maximum static);m;325;924
Maximum power output;MW;1,060;9,018
Max power per generator;MW;265;750
Flow rate;;;
– generating;m3/s;412;1,133
– pumping;m3/s;320;595
Storage;m3;12,000,000;238,800,000
Headrace tunnels;;;
– number;;2;3
– length;m;825;53,000
– diameter;m;6.2;12.7
The figure on page 7 here is interesting: http://www.seai.ie/Renewables/Renewable_Energy_Policy/Policy_Initiatives/Electricity_Storage_Event/Paul_Dean.pdf
It shows how development of pumped hydro has correlated with development of nuclear historically.
Would the correlation of nuclear and pumped storage have anything to do with the problems of integrating inflexible nuclear power stations into the grid?
The inflexibility of nuclear and the need to find demand in off-peak times is something that often seems to be ignored in the nuclear debate.
Hawkemoon,
The economics drives the choice of technologies. The least cost option is to make nuclear baseload only (get the most electricity for the capital cost invested) and build pumped hydro storage (where practicable) to provide the flexibility. Where sufficient pumped hydro storage is not available, economically, then we find the least cost alternative way to provide the needed flexibility from other options such as load-following nuclear, gas and/or coal.
The key point to understand is that pumped hydro is far too expensive to be viable as a support for expensive, intermittent, unreliable unscheduled renewable energy. The reason is explained in my comment @ 14 August 2011 at 8:43 PM.
If you are genuinely seeking a better understanding, you may find the lead article and comments on this thread valuable.
Storage of the sustainable such as wind and wave, geothermal, solar, remote locations is best done using pumped hydro’s first cousin compressed air. The second cousin, hydrogen, would also use pipes. Over time, pipe costs will not be too expensive, especially when we interface the energy pipes with mono rail and other needs. Consider a compare and contrast, that pushing water up, and then pushing air down (under water at sea to pressurize), are very similar in concept. http://www.environmentalfisherman.com The Tripe (track-pipe) System report. 11 pages illustrated.
I think too that hydrogen, expensive and difficult as it may be has enormous potential to be our miracle fuel. If we can think of hydrogen potentially as frozen electricity, transmitted by pipe, not wires, this may help us to justify working more diligently on hydrogen system proposals, and get us out of the bad habit of defaulting back to the fossil fuels. When we crack water we get hydrogen and oxygen, both usable fuels. ORCA, (oxygen rich compressed air) can be very helpful in hybrid gasoline and compressed air hybrid cars. We have a need for higher quality brainstorming, along with a willingness to push technologies forward. We haven’t maxed out on fossil fuel efficiency either, so I’m not saying give that a rest, but the directed need is for practical storage or conversions delivery etc. for our many good sustainable energy systems. Let’s look for the common denominators, non electrical, for future energy systems. What, or how does compressed air, (CAES) (ORCA), and hydrogen, and or other generated gases and liquids, or even pipe ready pellets, …. What do these have in common, and how do we invent the interfaces with the existing fossil fuels based and smart electrical grid based systems?
This is the wiser question rather than putting all hope and research into the electrical grid systems.
Hawkmoon, on 23 August 2011 at 1:29 PM — Gen II nuclear reactors were originally designed to provide nearly constant power. In fact, those units can be (and are) cycled for load-following; most of the data is from France.
The newest Gen III+ designs are prefectly capable of load following although even these newer units will operate to provide lower cost electricity if run nearly flat out. However, as I see the economics, while there may be a few locations where pumped hydro is economic, in most regions using the newer NPPs for load following is the most economic alternative.
@Peter Lang,
In point 3 on 23 August 2011 at 10:54 AM you said:
“The information about the variable speed turbines is interesting. They are used for controlling fluctuations in grid power. This is definitely not a plant designed for or useable with the variable power output from intermittent renewable energy generators like solar and wind power.”
Having read the article, I think it’s ambiguous at best. The following comment from the article:
“Asynchronous machines make it possible to regulate power not only in turbine mode but also in pumping mode. The range of control at Goldisthal amounts to 190 mw to 290 mw.”
and further reading of this article:
http://infoscience.epfl.ch/record/134078/files/asamihppaiaftegs.pdf
suggest to me that variable speed units, whilst unable to vary all the way down to zero active power, have a broader operating power range in both pumping and generating mode than their synchronous counter-parts. They also, as you say, seem to have a few more strings to their bow with regard to providing ancillary services.
I’m still getting my head around the power issues with sync and async machines, and indeed active and reactive power (my AC theory is very weak), but it does seem to me that variable speed pumped hydro units have some distinct advantages in a grid environment with strong fluctuations.
MickH,
Thank you for your comment and the link you provided. My comment you replied to is necessarily simplified for posting on a web site like this. It also assumes a lot of background from previous posts on BNC, the lead article on this thread and my previous comment here: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-133008 . In response to your comment I’d make the following points:
While intermittent renewables, like wind, are a small proportion of total generation, during pumping hours, the variability can be accommodated by the variability of the variable speed pump turbines. However, when the wind penetration is high, as is advocated by renewable energy advocates, the variability cannot be handled by variable speed pumped hydro units. This is one reason it is wrong to argue that projects like Tantangara-Blowering could be used to make wind power viable at high wind penetration (as Beyond Zero Emissions advocates).
Solar power is generated during the day. At this time hydro is generating or on standby, not pumping, so solar energy will not be stored. Furthermore, it is very high cost electricity so unsuitable for pumping (see comment linked above).
Wind power is high cost, so the economics are not favourable for pump storage. You wouldn’t consider building wind power or pumped hydro storage unless wind power is mandated. It wouldn’t make economic sense.
Furthermore, wind power is highly variable. That imposes additional costs on the system.
The most important point I can make is that there is little value in discussing possible technological solutions without looking at the overall economics and financing aspects.
Another trick I learned with variable speed water pumping (on a pond system) was to replace impeller type pumps with positive displacement types eg helical rotor for large volumes. Impeller pumps don’t like changes in intake water level (causing cavitation) or low r.pm. near stalling speeds when the water flows backwards. Helical pumps can go fast or slow though I understand they are less efficient.
My neighbour has an asynchronous or 3-phase squirrel cage generator on his mini hydro. I don’t fully understand the theory yet but I know some electrical settings have to be tuned for a particular water flow. I imagine that applies to pumping as well.
MickH,
Further to the last paragraph of my reply to you, “there is little value in discussing possible technological solutions without looking at the overall economics and financing aspects“, the cost of wind with pumped hydro as a means to provide reliable dispatchable power would cost roughly thirty times as much as conventional power generation: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-86108. So it totally uneconomic
Some important reasons why pump hydro storage is not suitable for intermittent renewables is summarised here: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-133008
I get it; if the nuclear proponents need-it/want-it that’s OK, but if the renewable proponents propose a solution it’s too expensive or not technically possible.
My father-in-law’s farm submersible wind/solar bore pumps a head of over 120m (I believe it go do 200m). Maybe the wide-diametre tunnel is the wrong approach; above ground pipes to covered/smaller reservoirs.
Zvyozdochka (@Zvyozdochka), on 29 August 2011 at 8:05 AM — Peter Lang has been looking at one particular proposed pumped hydro project. Some power stations stations, already in operation, are more versatile. The usual difficulty for gengizing by wind power is the lack of large storage; almost all existing pumped hydro stations are only appropriate for diurnal operation. Lack of wind power for an even moderately extended perior would put such a station out of business for the interim.
Follow the green line on
http://transmission.bpa.gov/business/operations/wind/baltwg.aspx
Following.
@ David B. Benson
I understand what you say but perhaps misreading what Peter is implying; are you Peter Lang, implying that pumps that can operate with a constantly variable input of energy (ie from wind) are not available?
As a technical challenge, why approach it with a massive diameter tunnel? Why not use tanks (like a lock) to raise the water step-by-step. I’d suggest it’s likely that the tanks themselves wouldn’t have to be huge, but perhaps large enough to stablise the next pump’s input draw.
Zvyozdochka (@Zvyozdochka), on 29 August 2011 at 1:23 PM — I’m not Peter Lang. It is standard practice to use variable rate pumps; done locally to pump groundwater. However, pumped hydro almost always uses a special king of pump/generator about which I know no more than such exist.
But even with a setup which can reverse every 15 minutes (as in a Franch pumped hydro facility), if you are out of overnight power you are out of business. Which is why nobody is seriously looking into such schemes.
@ David B. Benson
I apologise for accusing you of being Peter….
I thought the idea was to pump water from Blowering (lower) to Tantangara (upper) and then just let it run through Tumut 3. Why is it necessary to use 3-massively expensive new bored shafts forward/reverse to be the both the pumping path and power generation?
Obviously I’m missing something, but I can’t see why you wouldn’t just connect the two reservoirs over ground and drain through Tumut.
Zvyozdochka (@Zvyozdochka), on 30 August 2011 at 2:05 PM — You’ll have to ask Peter Lang. We don’t seem to have anything remotely comperable here in the USA.
Suggestions by Neil Howes and others that Tasmanian hydro stores excess energy generated on the mainland seem to be off the agenda. See the 4th paragraph in
http://www.themercury.com.au/article/2011/08/30/257231_tasmania-news.html
The present underwater HVDC cable is normally limited to 500 MW either way with minimum periods between flow reversals. The converter station on the Tasmanian end is close to an aluminium smelter and two gas fired power stations. The Victorian end is Loy Yang brown coal fired station, a candidate for replacement by combined cycle gas with the contract to be drawn by June 2012. Slight problem being lack of gas.
Clearly Tas dams have capacity for increased generation. The photogenic Strathgordon dam whose narrow ravine features in TV ads and sometimes on BNC has vacant mounting slots for two 150 MW Francis turbines. Evidently 3-4m rainfall the last couple of years is still below expectations. Another power source could easily pump outfall water back up to the lake to be recovered by existing or updated turbines.
John Newlands, on 30 August 2011 at 2:50 PM said:
Suggestions by Neil Howes and others that Tasmanian hydro stores excess energy generated on the mainland seem to be off the agenda. See the 4th paragraph in……
The data suggests that Tasmanian hydro already stores excess energy generated on the mainland, however presently most of that excess is off-peak coal -fired, returned during peak demand. Since TAS peak demand is about 500MW lower than present TAS hydro capacity, no need at present for additional HVDC links, but with more TAS wind capacity and more hydro capacity that could change. Of course future excess mainland electricity may be from wind, solar or nuclear rather than coal-fired.
David B. Benson, on 29 August 2011 at 8:29 AM said:
The usual difficulty for gengizing by wind power is the lack of large storage; almost all existing pumped hydro stations are only appropriate for diurnal operation. Lack of wind power for an even moderately extended perior would put such a station out of business for the interim.
Since most pumped hydro was built to even out diurnal fluctuations its not surprising. For BPA however, there is clearly enough hydro capacity and hydro storage for wind ( see the daily range in hydro). The problem is the transmission capacity for exporting surplus wind plus hydro in periods of high precipitation.
Follow the green line on
http://transmission.bpa.gov/business/operations/wind/baltwg.aspx
Neil Howes, on 30 August 2011 at 7:04 PM — I’ve followed the BPA situation quite closely. (1) Isn’t enough storage capacity. (2) Wind has to be curtailed in June. The problem has been partially resolved by almost 1 GW [nameplate] wind turbines shiftling from BPA balancing authority to the baancing authority to the south.
All this, of course, is off-topic on this pumped hydro threaed.
Neil to my knowledge recovery of water pumped uphill in Tasmania adds up to a mere 1.7 MW http://www.hydro.com.au/system/files/documents/PS_Factsheets/TodsCorner_Power_Station-Fact-Sheets.pdf
The Hydro plays the NEM spot market by selling hydro at peak times and re-importing coal power. You’d think carbon tax will make it preferable to conserve water in the dams. The other technique I believe is hydro balancing of wind so that hydro is throttled back when the wind is strong and vice versa.
http://www.transend.com.au/ournetworks/electricity/planning/windpower/
Despite claims that Australia has boundless gas I believe it will be unaffordable by 2050 so we’ll have to find some other way to balance windpower.
John Newlands, on 31 August 2011 at 6:08 AM said:
Neil to my knowledge recovery of water pumped uphill in Tasmania adds up to a mere 1.7 MW
I was not referring to pumped hydro but storing off-peak power from mainland by not using as much hydro locally during off-peak times.
The Hydro plays the NEM spot market by selling hydro at peak times and re-importing coal power. You’d think carbon tax will make it preferable to conserve water in the dams
A carbon tax isnt relevant while excess off-peak power is available. TAS hydro is going to generate the same number of kWhs/year it just makes more by selling at high peak prices.
Neil it’s alleged that the Comalco aluminium smelter and Nyrstar zinc smelter pay some 3-4c per kwhe, a subsidy against market rates claimed to be worth $133,000 per employee. If Loy Yang Vic produces 1.4 kg CO2 per kwh then 1.4 X 2.3c = 3.2c carbon tax, doubling the energy cost to the smelter if sourced this way.
What I don’t know is if there will be is enough local electricity in dry times to cover all Tasmania’s needs and whether there are escalator clauses in big supply contracts. A proposal for a silicon smelter near Burnie was nixed when carbon tax was first mentioned. I think several dams would suit pumping with minor modification but the Hydro seems uninterested.
John Newlands,
Off-peak prices on the NEM grid drop to $130( about the price that OCGT starts to come on-line). TAS off-peak demand is 6-800MW while TAS peak demand is usually 500MW less than hydro capacity so importing cheap off-peak mainland power and storing hydro to export at peak prices makes sense. The CO2 price is irrelevant because its a MWh/MWh swap, both off-peak and peak rates will rise. If TAS hydro is using the Bass-link at full capacity(500MW) pumped hydro adds no value, because they already have full flexibility.
Neil,
Is that a retail price? Data from AEMO suggests (in 2011) that the average wholesale price for the cheapest 7.5 hours of electricity each day is about $20 for VIC and about $21.60 for TAS. Are we talking about different things?
Zvyozdochka (@Zvyozdochka),
@ 29 August 2011 at 1:23 PM
No. I am saying you cannot change the flow direction and velocity of 20 million tonnes of water to suit the wind. Did you see this comment:
http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-133008
@ 30 August 2011 at 2:05 PM,
Read the lead article. The water is pumped up through the tunnels and runs back down through the tunnels to generate. Pumping is from about midnight to 6 am and geneation and standby is during the day, with maximum power output at peak times and in emergency.
The wter would not be released through Eucumbene reservoir, long tuinnels and three dams and power stations (Tumut 1, 2 and 3) on the Tumut River because around half the power would be lost in head loss.
The large diameter tunnels are needed to move the volume of water needed to generate the power. Power = hydraulic head x flow rate.
Surface pipes are far more costly that tunnels.
Really?
John Morgan,
Yes. The reasons are:
1. longer distance,
2. pumping needed to push water over elevations above the lowest level of the upper reservoir
3. Pipe has to be strong enough to resist negative internal pressure at high points.
4. Pipes have to be strong enough to withstand 10 MPa internal static pressure plus dynamic pressure at the lowest level. Conversely, the tunnel needs no lining except near the power station and in fault zones.
Refer to the discussions upthread about the cost of the steel liner for the surface power station option.
John Morgan, to see some comparative costs look at Table 1 in the lead article.
Surface pipes, at the lower levels (full pressure), cost about $1,000,000 a metre.
The tunnels cost about $65,000 a metre.
The steel pipe cost/metre is probably too low by at least a factor of two.
The pipes would be longer than the tunnels (probably 50% or more longer).
The tunnels need no lining for most of their length.
Thank you Peter. There’s a peculiar pleasure to be had from having one’s intuitions completely upended.
@ Peter Lang
Why not raise the water over the surface in a series of elevations, to tanks, like a ship lock? The pipes need only be strong enough to get to the next head. A college believes you could operate the pumping with a much wider range of power consumption as well (spare kWs to spare MWs).
Then you could have one drain/power tunnel that only ever operates in one direction.
Zvyozdochka,
Engineers look at all options and cost them. They select the least cost option that meets all the requirements. The fact that the vast majority of large pumped hydro schemes, especially high head schemes like this, use tunnels rather than surface pipes should be sufficent to convince you.
However, if you are not convinced, I’d suggest doing some simple calculations yourself. You can use the information in the lead article of this thread as a guide.
You might also ponder how you would transport the pipes to site and weld them on site. How do you weld steel pipes with 700mm wall thickness?
It is easy for people to pose all sorts of ideas but they need to be checked out before they are posted. Here is an example of one of the silliest ideas around at the moment:
http://www.solarserver.com/solar-magazine/solar-energy-system-of-the-month/hydraulic-hydro-storage.html
A quick check with anyone who knows anything about rock would have made them aware that this idea is totally impracticable. This is one of many such schemes being proposed by people who sit in front of computer screens but have no practical engineering experience.
I hope this reply will enable you to understand why I do not engage with you in depth on your various comments on this or the other threads.
“How do you weld steel pipes with 700mm wall thickness?”
Why would you distort what I say like that? If the pipes that raise the water in steps are NOT used as the power path (ie use one bored tunnel rather than three, one flow direction for drainage), the surface pipes that raise the water (in steps with smaller heads) don’t need to be 700mm thick.
Zvyozdochka,
Get someone to design and do the cost calculations for your proposed scheme. It is not in the ball park of being viable. There is no point in me wasting my time on totally hare-brained schemes. It’s just as hare brained as the one I linked to above.
Just think about it. This discussion started by arguing you want to be able to provide storage for wind power. You argued you could use reverseable pump-turbines so you could reverse the flow each time the wind changed. That is reverse the direction of 20 million tonnes of water flowing at up to 3 m/s.
Now you want to be able to pump up in one direction (in surface pipes) and let water down in the other (in tunnels). So you need all three tunnels for the flow in the down direction PLUS you want pipes, pumps and storage tanks for the upstream direction. You want thin walled steel pipes, pumps, and storage tanks at what vertical spacing? Say every 100m of vertical spacing. So you need say six pipes like the ones pictured in the Tumut 3 photo at the top of this thread. Each is about 80 km long, total 480 km of pipes plus the tunnels. And fifty four pumps and reservoirs.
Your proposed scheme is at least ten times the cost of the proposed conventional scheme. And this is being proposed to try and make wind power viable. This should be a wake up call about the sanity of those who promote wind energy and renewable energy.
Have you considered piping hydrogen from the Sun to Earth?
“You argued you could use reverseable pump-turbines so you could reverse the flow each time the wind changed.”
I made no such suggestion. I initially queried whether you were claiming that no pump existed that could operate with a variable/intermittent energy source.
After-that, I simply observed that it should be possible to use lightweight piping/tanks on the way “up” reserving a single large(r) tunnel on the way down.
Such a system could be capturing grid excess wind contributions continuously.
@ Peter Lang
“There is no point in me wasting my time on totally hare-brained schemes.”
Might I say that while you are good with your calculator and that is a plus, you are a magnitude of minuses on your advocacy.
Nuclear proponents need storage too, unless there is to be a massive overbuild of NPPs to meet the peak demand. This was the motivation behind the examination of a number of pumped storage schemes in the first place; capture the unused excess generation during the demand lows and use them during the peaks.
The alternative is to use some other low CF but high availability source during peaks, which usually turns out to be fossil fuelled.
The fact that proponents of renewables might wish to utilise such pumping storage schemes as well appears to irritate you endlessly. What a shame.
Zvyozdochka,
The problem is you just don’t take notice of what you are told if it doesn’;t agree with your preconceived ideas. You have little understanding of the subject matter and and seem unable to recognise the difference between 10% and 10 times difference between two options.
Yes, nuclear is cheaper if you use some storage for peak generation (every day). It is not essential, it is just cheaper to do it this way. But that is not the case for intermittent renewables. I explained why here: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-133008
That statement reveals you have no understanding of what is involved, and worse still you have not even bothered to try to understand the article at the top of the thread. If you have only one tunnel instead of three, you reduce the power by two-thirds, from 8 GW to 2.6 GW. Your lack of understanding or willingness to understand what you are being told, is why it is a waste of time trying to explain anything to you. You simply do not want to know. You just want to believe that wind must be good because …
Here http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-86108 I did a rough calculation showing that the cost of wind with pumped hydro storage to make it capable of meeting our energy demand would cost about 30 times the cost of nuclear. The scheme you propose would cost at least 300 times the cost of nuclear.
Your proposed pumped hydro scheme would cost:
$12 billion for the generating component (tunnels, power station, etc), Plus:
100 pump stations (6 pipes the size of Tumut 3 pipes and 12 lifts because we have to get over hills above the top reservoir level and there will be multiple ups and downs) . Each pump station will cost say $7 million. Total = $700 million for pumps.
Reservoirs: say $100 million
Pipes: Tumut 3 pipes are 500 m long and cost roughly $80 million in todays dollars; i.e. $160 million per km. We’d need say 80 km. Therefore, total cost of pipes = $128,000,000,000
Total cost of the pumping up component is $128,900,000,000 (say $129 billion.
Generating component = $12 billion
Total = $141 billion
Compared with about $12 billion for the proposed pumped hydro scheme (which is suitable for coal and nuclear but not for intermittent renewables for the reasons outlined in the link provided above)
This cost estimate is very rough (back of an envelope), but sufficient to show it is pointless investigating such ideas any further.
By the way, the Tantangara-Blowering scheme is unlikely to ever be viable, even for nuclear. The Tantangara-Talbingo scheme at about 6 GW may be more viable. However, none of these schemes would be considered until at least 50 % of our electricity was being supplied by nuclear.
I hope this clarifies this for you. I hope you will do your own rough cost calculations in future before posting your ideas.
“I hope you will do your own rough cost calculations in future before posting your ideas.”
Happy to. We will cost;
– 1 only bored tunnel w/equiv flow to 3x 12.7m tunnels
– required lightweight surface pipes to create 12 lifts to tanks using submersible pumps* over 12-18 hr period
It is my understanding that the Ludington Pumped Storage facility upgrades (Michigan) will use surface based piping in the manner I describe. It increases the plant flexibility.
* A recent project my US collegues consulted on uses some of the largest submersibles to lift 44-100m into tanks for stormwater control in Mexico City. They are sized for enormous and very sudden volumes. The pumps/piping/tanking per unit of pumping capability cost nothing like your statements.
How can you estimate the cost for a tunnel that is larger than the largest tunnel boring machine?
When I did the analysis I looked at combinations of two three and four tunnels and different tunnel diameters for each so I considered 9 options. If you reduce the total corss sectional area you increase the water velocity; this increases the head loss which means less power is generated and less revenue over the plant life. I used the least cost option. You can’t build one tunnel because there is no tunnel boring machine large enough to bore it (read the references in the article and learn a little background). You seem to think no one considers options.
You can’t use light weight steel if you want to raise water 100 m. And the steel thickness must be thicker as pipe diameter increases.
The costs I gave you would show any engineer that you are totally wasting your time. It shows me that you do not check out anything properly. You are running on belief that renewables are a good thing. just because they are! I’d urge you to get rational. You and those of suimilar ilk, such those who follow Climate Spectator, are doing Australia enormous damage.
I await your design that you claim will be cheaper than three tunnel option. By the way, just to cover my backside, I agree with comments up thread that the powerstation would have to be underground and the 6 GW Tantangara-Talbingo option may be more economic than Tantangara-Blowering.
PL this link gives some costs for the El Hierro 11 MW pumped storage system in the Canary Islands
http://gotpowered.com/2010/el-hierro-an-island-powered-entirely-by-renewables/
If I understand it right the image shows the upflow penstock and the downflow penstock side by side. Some key points are
– it integrates with desalination
– it’s small
– it is competing with diesel.
John, 11 MW, low head cannot be compared with 8 GW and 900 m head.
@ Peter Lang
Your “worldwide rock experience” reference does not link to a page so no-one can see what you were referring to.
Robbins Company have a 14.4m hard rock machine in use now for the Niagara Hydro Tunnel Project. They claim their design can go to 22-24m, recently discussed in the Berring Straight Tunnel speculation.
I see you choose to ignore my reference to a recent project undertaking by our company. Complete pump/pipe/tank costs on a cubic metre basis of head raised are nothing like your estimates.
“You and those of suimilar ilk, such those who follow Climate Spectator, are doing Australia enormous damage.”
Ilk? Our company is doing active work worldwide reducing emissions NOW on many projects, matching clients, investors and technology;
A project that has recently been given the go-ahead here in WA is a 50MW solar PV system (with diesel backup) via a fully commercial tendered PPA with audited emissions reduction claim for peak power production. It will be installed outside of Geraldton and be operating for 2013′s summer. The operator has options to supply a further 250MW.
How do you feel about that? Are we “damaging Australia”? Please.
Z@Z, do you have any links for the WA solar system referred to above?
Zvyozdochka,
Write up your proposed design and cost estimate. Then we can discuss it. Until then, further discussion is pointless.
In my opinion those advocating renewable energy, and blocking nuclear, are damaging Australia. In my opinion they are not being objective or rational. Your advocacy of a project that is totally uneconomic just because you want it to work is a typical example. People advocating renewables generally ignore the economic facts. I doubt you have even looked back at the references I gave in my earlier comments.
Those advocating renewables are usually the same people as those blocking nuclear. 50 years of blocking nuclear has caused it to be more expensive than it would be if progress had been allowed as in other industries. It also means that world emissions now are about 10% to 20% higher than they would be if nuclear development had not been thwarted. And we’d be on a much faster trajectory achieve low emisisons.
Your lack of ability to provide even the most basic cost estimates for what you advocate is common amongst renewable energy advocates, but demostrates how scary such irrational beliefs (such as in renewable energy) can be.
So my answer to your question is “yes”.
@ John Morgan
It’s fully commercial unfortunately, but here is one item of coverage;
http://www.energybusinessnews.com.au/2011/08/23/investec-banks-on-solar/
This report’s timings are slightly out and the project is already proceeding. Last I’d heard, full details will be available before year end as orders have been placed for the tracking CPV systems. It looks highly likely that the overall cost will be significantly lower than reported as well.
See LCOE estimate for PV component of Geraldton PV-diesel hybrid power station here: http://bravenewclimate.com/2011/08/28/open-thread-18/#comment-135561
Zvyozdochka @ 12 September 2011 at 1:38 PM
I don’t know which link you are referring to. Is it this one?
http://www.solarserver.com/solar-magazine/solar-energy-system-of-the-month/hydraulic-hydro-storage.html
It is working fine for me.
Barry,
Could you please change the link to “worldwide rock experience” in the lead article. It is under the sub heading “Cost Estimate”.
The last three letters “pdf” have been changed to “PDF”. The revised link is: http://www.rocscience.com/hoek/references/H2001b.PDF
@ Peter Lang
“11 MW, low head cannot be compared with 8 GW and 900 m head.”
The El Hierro head appears to be ~700m (http://en.wikipedia.org/wiki/El_Hierro#Energy).
What is your definition of “low”?
My mistake on the head for El Hierro.
I look forward to your cost estimates you said you will do for an 8GW Tantangara-Blowering pumped hydro scheme comparing all tunnel option with an option with tunnels for generating and surface pipes for pumping.
Volcanic islands that rise straight up out of the sea offer better elevation therefore need smaller volume upper reservoirs for the same stored energy. Thus pumped seawater hydro has been proposed for Hawaii and Reunion Island. In Australia we might be lucky to get 100-200m coastal elevation close to transmission. If I recall John Bennetts suggests the escarpment near Wollongong NSW. Fleurieu Peninsula near Adelaide might be OK but that area is NIMBY central.
Z@Z
Here http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-135527 I did a rough ‘back-of-an-envelope’ calculation of the cost of your suggested alterative to the Tantangara Blowering Pumped Hydro scheme.
My rough estimate for your suggested alternative was $141 billion
My estimate for Tantangara-Blowering (8GW minimum, 9GW average power) is about $12 to $15 billion.
I’ve done another very rough, calculation of your proposal by scaling up the cost of El Hiero from 11 MW to 9 GW (based on the El Hierro figures – $38 million for the pumped hydro component – given here: http://gotpowered.com/2010/el-hierro-an-island-powered-entirely-by-renewables/ (thanks John Newlands for that link).
This very rough estimate is $42 billion for a surface scheme. This is much lower than my first ball park estimate but still about three times the estimated cost of the underground alternative.
I look forward to your cost estimates for the two options: underground versus surface.
Just for interest:
The capital cost for the pumped hydro component is US$3450/kW.
The capital cost for the whole renewable energy scheme is US$4450/kW (does not include the desalination component)
Woops, this statement in my previous comment looks wrong:
It seems unlikely that 11 MW of wind capacity costs only $16 million Euro (US$22 million) which is $1450/kW. That is about half what I would expect it to be.
I expect the the capital cost for the whole renewable energy scheme is more likely to be around US$5,000 to $6,000/kW.
Current US wind farm installations are running around US$1725/kW capital costs, but I don’t know by how much that is lowered by various incentive schemes. Nor does that include the cost of new, long transmission lines.
David Benson,
Sources please. Total project cost divided by kW, for all US projects completed over the past 12 months. Doing that for Australia the average cost id $2750/kW. I doubt Australia’s costs are that much higher than US costs.
Overnight cost from
http://www.nrel.gov/analysis/tech_costs.html
Now for an example. A relatively speaking nearby 30 MW [nameplate] wind farm contracted with Idaho Power for an LCOE of US$0.091/kWh. Assuming 100% financing at US rates (15 years @ 8%), maximum CF of 26%, standard O&M (US$30/kW-yr), standard integration fee of US$0.005/kWh, and assuming Idaho production credit is the same as Washington state’s US$0.021/kWh, the project just breaks even at US$1800/kW.
Peter, thank you for that update.
My international colleagues (in their wisdom) have decided to make this a fully fledged project and estimate it ‘properly’.
Requests have gone out for the tunnelling component (RFQ to Grow Tunnelling and Skanska JV).
Current discussion revolves around the possibility of using composite pipes which are up to 40% cheaper than steel. (RFQ to Sekisui Chemical http://www.sekisuichemical.com/eslon/index.html).
We have the required turbine, pump and tank estimates.
Obviously our greatest unknown is the surface path and profile for works.
Will we get a credit for longer system life?? (Joking).
Zvyozdochka (@Zvyozdochka), on 14 September 2011 at 1:39 PM
Its worth considering a different option of a vertical shaft from Tantangara to an underground turbine room and a low pressure low incline tunnel to Blowering similar to the Kopswerk pumped hydro that is designed to handle variable wind power. This would eliminate the use of steel lined tunnels/pipelines.
http://www.hydroworld.com/index/display/article-display/0159389604/articles/hrhrw/hydroindustrynews/pumpedstoragehydro/austria_s-450-mw_kopswerk.html
Neil Howes,
You are correct that the power station has to be sited underground. This was discussed up thread. I explained than that my original analysis was intended as a simple analysis making use of the Tumut 3 costs and engineering features which I had access to and could scale up. I did not have any way to do a rough calculation of the cost of the underground siting.
The cost of high pressure surface pipes is far too expensive. Also, surface pipes are more vulnerable to environmental threats, such as land slides. At higher elevations there is the threat of freezing in winter if there is a period when the water is not flowing in the pipes.
You suggest the shaft should be located at the upstream end rather than near the downstream end. The choices are:
1. Long, high level pressure tunnel to shaft above the power station and short low pressure tailrace tunnel. In this case the tunnel would begin a little belo Tantangara’s minimum supply level and decline at about 2% slope to the top of the shaft. A surge tower would be above the shaft.
2. Short high pressure tunnel, shaft to deep underground power station, and long tailrace tunnel.
3. sloping tunnel from Tantangara to the underground power station and then a short tailrace tunnel. The power station would be as close to Blowering as is practicable. It must at about 300m depth below surface so there is sufficient weight of rock above to contain the 925 m of static water pressure plus dynamic pressure.
Which option is selected would be based on engineering design and costs of the various options. (the surface pipe option would also be considered in early options analysis, but I suspect would be ruled out at the prefeasibility stage).
Here are some issues that would be considered in the options analyses:
1. Geology, rock conditions, tunnel stability, tunnel support and leakage along the various possible routes.
2. Location and cost of the surge chambers
3. Tunnel length
4. Length of access tunnels to the tunnels (for construction and removal of the excavated rock). The longer and steeper the access tunnels the higher the cost of the project.
5. Length and gradient of the access tunnels to the underground power station. (these tunnels have be used to get the huge turbines, generators, transformers and other large equipment into the power station and for operation and maintenance for 60 to 100 years.
6. Hydraulic head loss in the low pressure tailrace tunnels. The tailrace tunnel must slope down from the Minimum Supply Level of Blowering Reservoir. So the power station would have to be located deeper if it is located far from the downstream end. This means the shaft must be longer. Long tailrace tunnels have to be larger diameter or more of them.
I would expect the cost difference between the highest and lowest cost underground option would be no more than 20%. Surface option would be probably 5 to 10 times higher than the underground options.
The best option will not be decided until well into the design stage. However, the difference between the various underground options will be small compared with big issues that you, Neil, are concerned about. The cost difference between the various underground options doesn’t make the slightest difference to the fact that a large pumped hydro scheme like this is totally uneconomic now, even for storing energy from cheap baseload power stations. When we get to the point that nuclear generates at least 50% of our baseload, it is cheap electricity, and is available every night during low demand periods, then a project like this may start becoming attractive. It will only be attractive if the cost of electricity with pumped hydro is cheaper than from load following nuclear. Pumped hydro may become a viable option sometime after 2030 at the earliest, IMO.
One thing for sure, as I’ve made clear many times before, pumped hydro will not be viable as back up for intermittent renewable energy in Australia. Wind and pumped hydro will be some 30 times more expensive than nuclear (ref: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/#comment-86108 )
If you want to argue that wind power can be a fully dispatchable electricity supplier, like fossil fuels, hydro and nuclear, then I suggest you cost wind generators with energy storage at site. That should be your starting point. Then you can get a good estimate of the true cost of wind generation.
Neil Howes,
Contrary to your statement that Kops II has a vertical shaft and the underground power station is located below the upper reservoir, this is not correct. Kops II is conventional layout [1]. The power station is located near the down stream end. There is a high level pressure tunnel, sloping pressure shaft, surge chambers, underground power station and tailrace tunnel. This is usually the least cost option and would probably be the least cost option for Tantangara-Blowering (if such a scheme with 53 km of headrace tunnel could ever be viable).
Just for interest, I’ve compared Kops II [1], [2]] and Tantangar-Blowering:
Capital cost; $ m;$545;$12,000
Power; MW; 450; 9,000
Capital cost; $/W; $1.21; $1.33
Generation p.a.; MWh; 614,000;
Capacity factory;; 16%;
Pressure tunnel:
length m 5552 53,000
diameter m 4.9 3 x 12.7
Water weight t 104,696 20,141,622
Note: In changing from generating to pumping mode, Kop II has to stop and reverse the flow of 100,000 tonnes and Tantangara-Blowering 20 million tonnes of water.
References:
[1] http://www.kopswerk2.at/downloads/Folder_061006_englisch.pdf
[2] http://www.hydroworld.com/index/display/article-display/0159389604/articles/hrhrw/hydroindustrynews/pumpedstoragehydro/austria_s-450-mw_kopswerk.html
This “Do the Maths” article on Pumped Hydro Energy Storage covers many bases and explains the key issues in easy to understand language.
http://physics.ucsd.edu/do-the-math/2011/11/pump-up-the-storage/#comment-1655
Australia’s pumped hydro not for renewables
There have been many comments on this thread about using Australia’s pumped hydro facilities to help make wind and solar power more viable.
A recent paper “100% renewable electricity for Australia’s NEM” by Elliston, Diesendorf and MacGilll http://www.ies.unsw.edu.au/docs/Solar2011-100percent.pdf demonstrates clearly that Australia’s pumped hydro plants could not help renewable energy much at the time it is most needed. (As explained in a number of comments up-thread there are also a number of reasons why the existing hydro facilities’ role and function in the NEM could not be diverted for the use envisaged by the wind and solar power advocates).
The objective of the paper is to show that a 100% renewable electricity system could reliably meet all of the NEM’s demand. In fact, it demonstrates the opposite.
Look at slide 12 in this slide presentation of the simulation study http://www.ceem.unsw.edu.au/content/userDocs/Solar2011-slides.pdf . There is no pumped hydro generation on 1, 2, 5 and 6 July, 2010. Those are the days where Wind + CST + PV could not provide sufficient energy to store energy at the CST plants, let alone in the pumped hydro plants.
This slide reveals much more too. For the period 1 to 6 July, the simulation would need gas generating capacity about equal to the winter peak demand. Ignore the hydo; it is wrong. Contrary to assumptions in the simulation, Australia’s total hydro capacity cannot be run at full power for days and weeks at a time (outside sun hours).
Retooling to green energy is proving to be a daunting task. If only we could figure out how to both store and ship energy … feasibly. I think I may have the answer, but my research is seat of the pants. My thinking is that we can plumb our energy, rather than depend on the fossil fuel related electrical transmission lines, entirely. CAES has major advantages in storage and shipment, using pipe. So once pipes are in place the location of CAES and hydrogen is not a factor. In fact using plenty of pipe, we gain storage, and we gain equilibrium, so transmission pumping energy drops to virtually zero. High pressures are a must to achieve these lofty goals, and also larger diameters than we’re used to. These pipes can also serve, and must serve other utility needs as well, just to justify the expense. That’s not a problem. We need a good monorail system. We could also do with a modernization of our rail systems, which can be augmented with this plumbing. My designs for track-pipe rail systems use steel to ground for most of the weight, but have two gauges of steel track and the wide pipe gauge would be for outriggers or light weight land yachts on rail, increasing tourism. Conduit pipe is a good idea in many respects in spite of naysayers who can’t fathom how the air gets compressed or can’t fathom how pumping or use conversions would work. These conduits are a super system which carries any and almost all of our major infrastructure needs: Water, Sewage, Natural Gas, Broadband, Granulated Plastics, and of course CAES and Hydrogen. So I have a feeling in addition to the major transportation infrastructure rebuild, these utilities would be carried by such a system, and financially carry it indeed. So many uses for a pipe. It’s the Track+Pipe concept, or TRIPE for short. CAES I’m sure could augment pumped hydro, and add to its viability. High pressure hydraulic systems tied to CAES are up and coming technologies, and a company SustainX is working on this. Peter, have a look please. http://www.environmentalfisherman.com
Steven Jf Scannell,
You need to estmate the cost of your proposal, and provide the basis of your estimate so we can understand it, or it is measningless. Look at the lead article on this thread and the twoo hundred comments on the thread to get some background as to how to approach that.
Without costs, your idea has about as much credibility as a proposal to pipe hydrogen from the Sun.
The following is an extract from a comment posted by EL on the “100% renewable electricity for Australia – the cost” thread http://bravenewclimate.com/2012/02/09/100-renewable-electricity-for-australia-the-cost/ . I’d like to post the questions and an edited version of the answer here for ease of finding comments on pumped hydro in future.
EL asked:
I’d like to expand on the comment here http://www.oz-energy-analysis.org/feed/show_me.php?comm=OzEA_DG0002 which addressed the question:
EDM-2011 cited this comment on OzEA as the basis of their pumped hydro energy storage capacity, but they did not realise there is a constraint on the rate at which energy can be stored.
In reply to EL’s comment about the rate at which energy can be stored in the three existing pumped hydro plants:
“20 GWh DOES reflect an upper storage limit”. This statement is correct.
“2.2 GW capacity”. No. That is not correct. Wivenhoe is the only pure pumped hydro scheme in Australia. The other two PHES plants have some pumped hydro capacity within a plant that is mainly a hydro plant. EDM-2011 attributed the full generating capacity of these plants to pumped hydro.
Only 0.9 GW of generating capacity can be attributed to pumped hydro. The remainder of the 2.2 GW EDM-2011 assumed should be attributed to hydro. Furthermore, there are energy losses in pumping and generating, so only about 75% to 80% the energy can be recovered.
Wivenhoe pumped hydro energy storage facility:
All the water Wivenhoe PHES plant uses to generate power must be pumped up from Wivenhoe reservoir. It can store energy (that is energy that can be recovered, after losses) at the rate of about 328 MWh per hour. It pumps when demand is low and electricity is cheap – between about midnight and 6 am (longer on weekends). It is on standby (spinning and ready to go to full power within less than 1 minute) for about 12 h per day and generating to meet peak and intermediate demand for about 7 hours per day (at variable power output). It generates a little during standby to balance power and frequency fluctuations in the grid. It cannot pump while it is generating or on standby. Because it is needed to be generating and on standby during the day, and because power is cheap at night, the pumping is done at night when the plant is unlikely to be needed for generation.
It takes a lot of energy to start pumping the water. The weight (~23,000 tonnes) of water must be lifted up 100 m against gravity and accelerated from 0 to 3.6 m/s velocity each time pumping starts. Therefore, it is not economic to repeatedly stop and start the pumping. The pumps are not variable speed so once started they run at their constant pumping rate of 207 m3/s.
Therefore, the pumps should only be started if they can be assured they will pump for at least several hours (e.g. 5 hours, but I said let’s assume a minimum of 4 hours to be economically viable).
If we assume an average of 5 hours of pumping time per day and energy storage at the rate of 328 MWh per h, then Wivenhoe can store about 1,640 MWh per day.
Tumut 3 has 1,500 MW of generating capacity in six generating units but only three have pumps and the power of the pumps is only little more than half the power of the generators. So it is not appropriate to assign the 1,500 MW of Tumut 3 generating capacity to PHES.
Bendeela & Kangaroo Valley – similar comment to Tumut 3.
See more details here:
http://www.oz-energy-analysis.org/feed/show_me.php?comm=OzEA_DG0002”
I’ve received questions recently about pumped hydro cost estimates. I’ll post the questions (edited) and my answers here for the benefit of others:
My reply:
Thank you for your question. I do not have recent cost figures.
What I can tell you is the cost of pumped hydro is very site specific. By “very” I mean order of magnitude. So realistically, unless you are dealing with a specific site, any cost estimates would be next to useless.
You asked for ‘ball park’ cost in $/MW. That is one of the unit costs. But the other you would need, if your interested is in energy storage for renewable energy, is $/MWh of energy storage capacity. Because, with renewable energy, the important parameter is how much energy you can store, not how much power you can generate.
This site gives a broad range of costs (both $/kW and $/kWh) for pumped hydro in the USA:
http://www.electricitystorage.org/technology/storage_technologies/technology_comparison
Here are some tools that can help with cost estimating, but you would need an engineer with a great deal of experience in hydro to assist with the data input.
http://hydrohelp.ca/eng/home.htm
Lastly, in this paper posted on 10 February 2012
http://bravenewclimate.com/2012/02/09/100-renewable-electricity-for-australia-the-cost/, I made a crude cost estimate for the “100% renewable electric NEM” system analysed by Elliston et al. (2011). My critique of the Elliston et al. paper provides some comments on the Australian pumped hydro storage capacity and the rate that energy can be stored.
Few people realise that pumped hydro has its place when matched with low cost base load power supply, but is most unlikely to be economic for storing renewable energy.
I do not have recent costs for the mechanical and electrical equipment. However, I’d caution against the approach where you start by estimating the cost of items that are a small component of the total cost and then look at the sensitivity to the high cost items. Other than adding a small pumped hydro facility to an existing dam, the costs of the civil works will dominate the costs as Table 1 in the Tantangara-Blowring post shows (the pumps, turbines, generators and transformers comprise about 5% of the total cost in that estimate).
I’d tend to start with the item that is the highest cost as the first step. There is no “general” price for pumped hydro. The cost depends on the hydraulic head (the elevation difference between the minimum operating level in the upper reservoir and the full supply level in the lower reservoir), the distance between the outlet from the upper reservoir and the lower reservoir, the length of tunnels or surface pipes, the length and thickness of steel pipes ( a very high cost item), and the minimum amount of storage available in smaller reservoir.
By the way, please note that the Tantangara-Blowering reservoir was purely and exercise to reveal the costs, and what is involved in the costs. The capital cost figure I derived is too low by at least a factor of two, as the two reviewers’ comments at the end of the post show. I expect the cost would be in the order of $15 billion. However, there is no way that the Tantangara Blowering pumped hydro scheme could be viable. It is not viable physically nor financially. It is not viable physically because of the time and power that would be required to stop and start the flow of 20 million tonnes of water moving at 3 m/s in the tunnels each time pumping had to stop and start. Think about the power and energy needed to accelerate 20 million tonnes to 3 m/s. That would be equivalent of having one tug boat at the head of a line of 100 fully loaded 200,000 tonne ships and trying to accelerate them to 11 km/h
Yes. I suspect you are correct on that point.
OK, Energy = 1/2 * m * v^2
20 * 10^6 * 10^3 kg * (3 m/s)^2 = 10 * 9 * 10^9 J = 90 GW.s
Which is a lot, but is also only 10 s of full power output, or 20 s of charging input.
Another perspective, use energy = pressure * volume. If the pumps can manage ~5 bar/50m head/0.5 MPa above the hydrostatic 875 m head to accelerate the water, they need to pump 90 GJ / 0.5 MPa = 180,000 m^3 of water to supply the kinetic energy. At a total cross section of 380 m^2, that’s ~473 m of movement. Call it 0.5 km. If the acceleration is steady from standstill to 3 m/s, the average speed during that time will be 1.5 m/s, so it will take 500/1.5 = 333 s, ~5.5 minutes to start up. This seems unrealistic for something so large, so maybe it’s only 1 bar of overpressure available, for a 30 minute startup. Doesn’t look inherently unworkable on these grounds.
Luke_UK,
This is an excellent reality check. Very elegant. Thank you.
i.e. 9 GW for 10 s or 4.5 GW for 20 s.
In terms of power I think it is more manageable than this because there are three tunnels. I expect they would be started one at a time. Therefore, we’d need 3 GW for 10 s or 1.5 GW for 20 s (if the pumps had the capability to accelerate the mass of water in that time).
However, as you imply, the pumps would not have the power to provide this acceleration in addition to lifting the water against 875 m of hydraulic head. Hence your second “perspective”.
I’ve redone your calculations for the situation with three tunnels. I calculate the time to accelerate the water in each tunnel would be the same as you calculated – say 30 minutes – but the three tunnels would probably not be started in parallel. So the start up time to full pumping rate would probably be longer, and perhaps up to 90 minutes.
This seems to me to be an excessively long duration for pumped hydro. As far as I know the big pumps that would be needed on a project like this have to run at constant speed. So, I suspect a long acceleration time is unlikely to be viable (however, this is outside my area of expertise). I’d note that most hydro plants boast they can go from zero to full power generation in less than a minute. I am not sure how long the pumps take to start. Perhaps someone else could comment.
My gut feeling remains that a pumped hydro scheme with 53 km of tunnel and 875 m of head is not viable. For comparison, Tumut 3 has 488 m of surface penstock (i.e. steel pipes) and 150 m of head. Wivenhoe has 420 m of tunnel and 100 m of head (from memory). Therefore, the Tantangara-Blowring tunnel is more than 100 times as long and the hydraulic head is about 6-10 times greater than Wivenhoe and Tumut 3.
Peter Lang — I’m a bit unsure about what you are enquiring, however even big pumps can use induction motors and so run at variable speed. For highest electrical efficiency synchronous motors are used and those run at only one speed under load.
The synchronous generators in the dams around here are rescheduled every five minutes and I’m not sure how much less time than that the units could be started or stopped. The ones I’ve seen rotate quite slowly despite generating around 200 MW each. In any case BPA routinely ramps in excess of 400 MW each rescheduling interval (but of course has many individual generators to participate in this load following).
Grand Coulee dam has has six pump-generators to deliver irrigation water (and someday do some peaking power gneration). These are of a design similar to the generators although only about 50MW each.
DBB, Your examples are not applicable at all. They are of a totally different scale – orders of magnitude difference. Could I urge you to reread the lead article and the particular comments you are responding to with a particluar aim of getting a feel for the scale of what we are talking about. Then you might want to look for examples of pumped hydro schemes with 53 km tunnel length, 12.7 m diameter, 900 m of hydralulic head, 8-9 GW generating capacity and see if you can find anything that might be relevant?
The latest in large-scale engineering technology are variable speed machines for greater efficiency. These machines generate in synchronization with the network frequency, but operate asynchronously (independent of the network frequency) as motor-pumps. from
http://en.wikipedia.org/wiki/Pumped-storage_hydroelectricity
and which I take to refer to induction motor-generators connected to the switchyard via power electronics. The technology is quite similar to that used in wind turbines [but of course the wind turbines are just used as generators]. The critical element is the power electronics but these can be made arbitrarily large, being not much more than a form of highly efficient rectifier/inverter pair. One could even put an HVDC line between the two ends if desired.
From
http://en.wikipedia.org/wiki/Francis_turbine
the highest head utilized so far is around 700 meters; I have no way to estimate whether operating with a 900 meter head is even possible with currently available materials.
The remaining issue is the valves used to control flow rates while generating. Again that great head height may be a concern. For smaller projects it seems that starting in under a minute is possible [from the first wiki article]. So one possiblity is to provide several smaller pump-generators, each with its own tunnel; only a suggestion.
In any case, I don’t see (so far) any insuperable difficulty regarding the electrical aspects. But as earlier comments have discussed, inertia means that flow is not going to quickly reverse.
DBB, You are mixing apples and rocks.
This is meaningless. What does it mean in the context of the pumped hydro we are talking about. Can I urge you to put the bits and pieces you come up with together. Otherwise it a bit like saying “an Atlas rocket is really big, but a Holden car is one of our biggest cars”. It’s just meaningless bits and pieces of unrelated snippets.
Peter Lang — I explained already following the link to the quoted wiki page: once again, this is an induction motor-generator with power electronics to allow for variable speed operation.
I don’t see why the three tunnels should not be started at least partially in parallel. Even for a 5-minute start, the peak acceleration power is only 12% of the full-rate pumping power, and for 30-minute startup only 2%. The simplest option would seem to be to let the pumps run up until the total power is the designed 1.5 GW/tunnel, then leave the flow rate to asymptotically approach 3 m/s at constant power draw.
For the nuclear + hydro case, how fast would you want to ramp up? You start with all the reactors running at near capacity and demand falling in the late evening. From the demand graph above the load ramp rate is about 1250 MW/hr, so you start the pumps at 23:00 but have to wait until 02:30 for there to be enough spare power to run at full rate. Then you ramp back down more steeply from 06:00 to 07:30. This scheme is so big, 18% of the average grid load, that it is constrained to move slowly to avoid over-stressing the grid it is meant to serve.
A possible error – is the 3 m/s flow rate for the discharge or recharge step? Back-of-envelope calculation gives 4.5 GW recharge as only 1.5 m/s, so all the energy and power estimates drop by a factor of 4.
Luke_UK,
Good point. The 3 m/s is for discharge not recharge. I haven’t calculated the rate for recharge, but I’ll take your figure as probably correct.
You make a good point about the additional power needed for acceleration (i.e. additional to the power needed for constant rate pumping) is only 2% for 30 minutes acceleration period or 12% for 5 minute acceleration period.
However, I am still not sure about the capability of pumps to accelerate 7 million tonnes of water (per tunnel). I understand the pump’s speed is synchronised to the grid then begins pumping and its speed stays constant throughout. So I am not sure if it is feasible to accelerate the flow over a long period. I know very little about this, but I still wonder about accelerating this mass of water given that existing pumped hydro schemes have only relatively short tunnels.
You’ll notice on the map in the lead article the dog leg in the tunnel alignment. That is a high point in the surface topography and the best location for the surge shaft. I wonder how high the surge shaft would have to be above ground level to accommodate the surge caused by the relatively long duration acceleration and decelerations we are considering. Calculating this would be beyond my capability. Of course, this is just an added cost so it is does not preclude the concept. Also, there may be other ways, such as an underground pressure chamber instead. Again, just an additional cost.
For DBB, variable speed pumps are not used in large pumped hydro faculties, although they may become viable in the future. I’ve commented on some pumped hydro plants in Japan and Europe in previous comments on this thread.
Having a surge shaft near the low end will make startup a fair bit easier, as it is then unnecessary to accelerate the whole mass of water together. Some checking on Google maps finds several points in the region to the east of Tantangara where ground level is well above the level of Blowering, Assuming that tunnelling there is possible, there is plenty of scope to get the water level in the shaft several tens of metres above hydrostatic equilibrium, which is all the overpressure required for any reasonable startup time.
The major issue, though, is how to manage the necessary ‘slip’ between the turbine rotor moving at full speed as required for grid synchrony and the water which is initially not moving at all. At startup the impeller blades have to move through the near-stationary water, while nearly all their swept volume goes around their edges. During normal pumping, or generation, running at only slightly lower pressure than the startup pressure, there can be only a few percent of the swept volume leaking past the blades if acceptable efficiency is to be achieved. I can’t think how this could be done with a fixed geometry for the rotor and housing. There has to be some way of allowing more bypass during startup. This problem is not unique to this scheme, and must have been solved for other pumped storage sysyems
Too much speculation here, I don’t think we can get much further unless a turbine designer comes along to help.
Just enjoying the great brainstorming here. Perhaps very high pressure compressed air could both cheaply jump start the impeller, and using a temporary seal, far up the pipeline, we could vastly increase the water pressure, and velocity, just temporarily, to get the system up to efficient speed, cheaply.
I don’t know if there has been any experimentation with a hybrid low head pumped hydro, along with CAES. But this may make sense, just to toy around with the idea. Since wind and wave generated compressed air could augment any pumped hydro system. In theory it may be a good marriage. Both the wind and water supply can be fickle, and each could hedge each other, again in theory.
Since the most efficient storage of compressed air, to me, is at depth at sea, then the problem of distance would need to be overcome with pipe diameter, which should not be a problem. At sea CAES means little to no wiring and all the distance issues with transmission. Pipe is cheap, but pipe dreams are cheaper. http://www.environmentalfisherman.com