.png)
Below I reproduce our first serious modelling work on Oz-Energy-Analysis.org (see this BNC post for a description of OzEA, including its goals and Open Science methods). The work presented here is high level and abstracted, and will be developed in future rounds.We’re looking for hard-nosed comments/critiques, and suggestions for current and future directions (especially over at the OzEA site, where we want the action to start happening). We want our assumptions and simplifications to be ‘road tested’ by heavy traffic. Go on, savage us (if you can)!
Note that before you read the below, it would be helpful to catch up on a bit of the history of the development of these ideas. The ideal OzEA posts to read, in evolutionary order, are:
Reconcile Wind Farm output with BoM wind data
Gross Variability of SA Wind Power
First Analysis of Wind Penetration
(Don’t worry, they’re all fairly short and the background reading shouldn’t take you more than about 20 min).
———————————————————-
Large-scale wind power using a bucket storage model and gas backup
ABSTRACT
We model the use of Wind Power, Gas Turbines and Storage to supply electricity as required to meet a demand curve at an hourly time resolution. For the demand curve and the wind power we use historical data from South Australia (SA) in 2009. The gas power and the storage are both idealised, the aim here being to, first, lay the groundwork for later models, and second, to examine the basic dynamics of a power system based on Wind, Gas and Storage.
INTRODUCTION
Building from the analysis of wind penetration, and simplifying as described on the models cover page, we implement a high level model of storage dynamics, and also gas turbines, such that wind, gas and storage combine to supply the demand for electricity. We consider the SA grid to be isolated except insomuch as the storage we include here abstracts the interstate connectors.
To model a desired amount of Installed Wind we simply scale up from historical data. To get the demand left after Wind Power (as in Figure WP2 from Analysis / Wind Penetration) it is straightforward to step through the historical data (hour by hour, 8760 of them per year) and subtract the wind power from the demand to give a remainder. It is this remaining demand that we need to supply using Storage and Gas Turbines.
In the first instance (Results, part 1) we introduce a simple storage model such that when the wind power exceeds the demand, the excess can be stored (up to some limits) and then used later. Then (Results, part 2) we include Gas Turbines, such that demand is supplied by three components: (i) available wind power, (ii) gas power, and (iii) drawing down storage reserves. Both the wind and the gas can ‘charge up’ the storage.
The storage model is very simple (abstracted). We conceptualise storage as a bucket of a certain size (the Storage Capacity), and with two pipes – one for filling the bucket, one for draining the bucket. So, when the Wind Power exceeds Demand, the excess electricity goes into storage at a rate no higher than the input ‘pipe’ allows, and only while there is room left in the bucket. When Wind Power is less than the Demand, electricity flows to demand from the pipe at the bottom of the bucket (either dumbly, or somewhat intelligently when we include the gas turbines). In all cases the three parameters that describe the storage model remain as the total capacity, the maximum input rate, and the maximum output rate. As this stage we ignore storage losses and make the input and output pipes the same size.
Adding gas turbines to the model is more complicated that it might first seem. Let’s back up a step; when using storage to capture excess wind power it is simple (as above) to add and subtract from the storage, but with gas turbines included the role of storage is not just to capture excess wind power, but also to smooth the ups and downs to use the gas power as evenly as possible. That is, when the unmet (after wind) demand is high, we want to draw from available storage, and when the unmet demand is low we may want the gas turbines to work on charging up the storage in preparation for the next days peak demand.
Managing the use of gas turbines in a real grid is more complex than we consider here at this stage. Here we use a simple heuristic algorithm to do this (described in the methods below). While the details of this heuristic are important, and will be developed, it is recommended that readers avoid getting bogged in this before appreciating the broad view. What matters is that the results we obtain, at every hour point, have supply meeting demand (and the constraints of the storage model respected). The heuristic achieves this, and otherwise provides a suitable basis for this starting model.
Finally, note that average demand in SA 2009 was close to 1.5 GW. In part 1 (Results) we consider increasing levels of Installed Wind, and quantify how much of the overall demand can be meet with different storage cases. You can think about this in multiples of average demand; that is, 3 GW installed wind is twice average demand, 4.5 GW is thrice times, etc. In part 2 we fix on a constant value for the installed wind at 3 GW Installed Capacity, which is twice the average demand, and which has a ~30% Capacity Factor and so translates into a little over 50% penetration (depending on the storage model / amount of spill).
METHODS
The basic model is that, at every time point, Supply = Demand. In this work Supply and Demand can be broken down with the following categories and nomenclature:
Demand = Overall Demand that must be supplied.
DS = Delta_Storage; +ve when power flows into
(charges up) storage, -ve when drawn down.
Spill = Spill; this is any power (usually Wind Power)
that is not used
WFS = Wind Farm Supply
FFS = Gas (Fossil Fuel) Supply
With which we can write down the basic equation of this model:
Demand + DS + Spill = WFS + FFS (*)
In addition to requiring (*) to hold at every time point, the Storage model imposes constraints. There is a maximum storage capacity, and maximum values for the flows in and out of storage.
Within these requirements there are as many different ‘solutions’ as you care to carve out; while the WFS is defined for us, how gas power and storage are utilised to make up the remainder admits many possibilities. In a general sense some of these possibilities are better than others because we recognise the intelligent use of storage in shaving the demand peaks, and also the desirability of a smoothly varying gas power requirement. Thus (at this stage at least) we do not attempt to solve this problem in some mathematically optimal way; rather we seek to solve it in some simple and reasonable way. What follows is the simplest useful approach I could muster; it is based around a ‘dumb’ starting solution that is ‘annealed’ into a more reasonable solution.
The Dumb Starting Solution (the Bucket Storage Model)
First up we simply run the bucket model of storage, as above, using the given ‘Dem’ and ‘WFS’ curves to solve for ‘DS’ and Spill, which in turn allows us to solve for the required FFS. Explicitly: if the WFS is greater than the demand, then the excess power goes into storage up to the maximum rate and maximum capacity (any WFS remaining is spilt); if WFS is less than demand, then the shortfall is made up, as much as possible, from storage (with any demand remainder being supplied by FFS). In this way a valid starting solution is obtained. Note that this solution is not making smart use of the storage (not holding it in store for peak demand times), and it is not using the low demand times to ‘charge up’ (with FFS) the storage in preparation for the demand peaks.
The Annealed Solution
This is an iterative three step process; I simply describe the process and ask the reader to note that so long as (*) is satisfied at every time point, and so long as the final solution is useful, then there is little to argue about. If you understand how this works, and / or if you are able to suggest or provide better methods, then I am most interested to hear. If you do not understand how this works (and want to) you should read up on Simulated Annealing.
Step 1. Since our goal is to smooth out the ‘remainder’ curve (i.e. the FFS), we apply a simple filter (a three point moving average here) to the previous FFS curve, and call this the wished_for_FFS, or simply wFFS (and we will also have wDS).
Step 2. Since our goal is to use low demand times to charge the storage in preparation for the high demand times, we add a random component to each wFFS value that preferentially moves it towards the mean FFS value. This random component is applied in the style of a simulated annealing algorithm in that: (i) for early rounds, the random components are larger (up to 10% of the mean FFS) and these are only mildly biased towards the centre; (ii) as the annealing progresses, the application of a ‘cooling schedule’ means that at each iteration the random components are (on average) a little smaller than previously, and the central biasing tendency a little stronger.
Step 3. Run ‘the enforcer’ to ensure that (*) and the storage constraints are respected. At each time point take the Demand, the WFS and the (wished for) wFFS (i.e. the FFS result for that time point from the previous steps) and calculates the ‘the remainder’ (i.e. Demand – WFS – wFFS); if this remainder can be supplied (absorbed) by the storage then the wFFS value is accepted (and the DS and any spill is calculated). Otherwise, wFFS is adjusted back to the nearest value that allows a legal solution to (*).
The above steps are iterated a large number of times (1000 at the moment) to give the FFS and storage curves seen in this work.
RESULTS
Part 1. The Basic Dynamics of Storage and Wind Penetration
In the basic implementation of the Bucket Storage Model, excess wind power is stored (up to the capacities of both the bucket and the input ‘pipe’), and this stored power flows to demand when wind power is less than demand (conceptualised as flowing to demand from the ‘pipe’ at the bottom of the bucket).
Following on from Analysis / Wind Penetration, we examine the Wind Penetration curves under the following versions (parameterisations) of the Bucket Storage model:
storage Capacity pipe size
(GWh) (GW)
-----------------------------------------
No Storage 0 0
Storage 1 5 0.5
Storage 2 20 1.0
Storage 3 50 2.0
TABLE M1-1: Storage model parameterisations for the first round of modelling.
As previously, we are using the SA 2009 historical data, for which the average demand is close to 1.5 GW, and where the Wind Farm data has a Capacity Factor of close to 30%. The Wind Penetration (i.e. the overall percentage of demand provided for by Wind Power) is considering at increasing levels of installed capacity, modelled by scaling up historical Wind Farm output data. In Figure M1-1 we see how the different storage models allow the Wind Penetration to obtain higher values before the diminishing return of significant lost (spilt) power kicks in.
Figure M1-1: Wind Penetration with Storage. The percentage of demand met for increasing levels of installed wind power under the various storage cases. Based on SA demand and Wind Farm data, 2009.
We now perform a simple sensitivity analysis. Treating No-Storage and Storage-3 as bounding cases, we examine how the Storage-1 and Storage-2 cases respond to changes in, first, the overall Storage Capacity (while holding the Pipe Sizes constant), and then examine changing the Pipe Sizes (while holding the total Storage Capacity constant), as shown in (Figure M1-2). In all cases the variable being examined is halved and doubled in order to define the shaded regions shown.
Figure M1-2: Sensitivity Analysis (for the Storage-1 and Storage-2 curves from Figure M1-1). In the left panel the pipe sizes are held constant and sensitivity of the penetration value to changes in the maximum storage capacity from one half to double the value in Table M1-1 is shown shaded. Similarly for the right panel but with the maximum storage capacity help constant, and a half to double range applied to the Pipe size.
It is not surprising to observe sensitivity to a doubling or halving of the total Storage Capacity (left panel); what is noteworthy is the lack of sensitivity to the Pipe Size (right panel). For both the Storage-1 case (5 GWh Capacity, 500 MW pipes) and the Storage-2 case (20 GWh, 1 GW), doubling the pipe sizes does very little, and halving them not much either. It seems apparent that the lower frequency changes in the Wind power dominate the storage requirementswhen the concern is achieving minimal spill at high levels of installed capacity.
Part 2. Modelling the Gas Supply (first attempt)
Now we explicitly treat the use of gas turbines to provide the remaining (and controlled) power we need to balance the system. For this we work with a single value of the Installed Wind Capacity at 3 GW (this being twice the average demand of 1.5 GW, and subject to a capacity factor of ~30%), and corresponding to a penetration of around 50% (depending on the storage model).
We use the methods described above to (somewhat) intelligently schedule the gas power so as to utilise the storage for peak shaving (i.e. at low demand times, more power than needed is produced and the excess is used to ‘charge up’ the storage for drawing down at times of high demand). This is shown for the Storage-2 case, and for a Jan 2009 (first month) slice of the data, in Figure M1-2 below; the full results, for the whole year, are here given for Storage-0,Storage-1, Storage-2, and Storage-3. A few minutes looking at these numbers can help reveal the complexities involved in cleverly scheduling the gas turbines; but the reader is also cautioned against getting stuck on this aspect (i.e. fixating on trees without taking time to appreciate the forest).
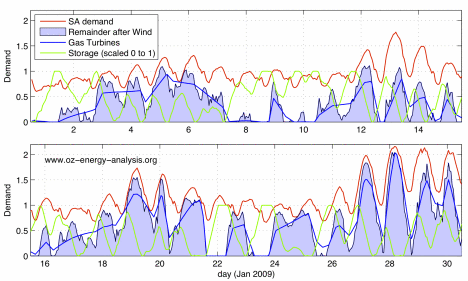A. Storage-1 (5 GWh max Capacity; 500 MW ‘Pipes’)
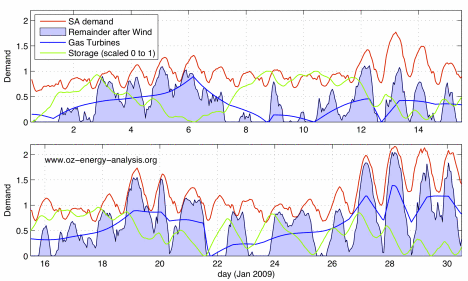B. Storage-2 (20 GWh max Capacity; 1 GW ‘Pipes’)
Figure M1-3: Scheduling Gas Power with Storage. Model results (shown for Jan 2009) for the Storage-1 case (top panel A), and the Storage-2 case (bottom panel B). Based on SA demand and Wind Farm data (scaled up to 3 GW Installed Capacity). NOTE that the ‘Demand’ axis has been scaled so the mean SA demand (1538 MW) = 1. Also, the storage curve (green) is scaled from 0 to 1 covering empty to the Maximun Capacity as given by the storage model.
———————————————————-
This is mission accomplished for here and now — to run a simplified model of supply meeting demand.
From here we want to:
(i) Look specifically at the problem of scheduling combined cycle and open cycle (peaking) gas turbines to meet a demand curve;
(ii) Look at ‘The Bucket’ in more detail; specifically, to look at the NEM states collectively (as individual units piped together).
Please consider this work as a starting point, as something we will build on as we develop through to costed scenarios.
Filed under: Renewables
A couple more graphs may shed further light. Firstly an hourly cost curve. I think the figure of 10c per kwh or $100 per Mwh is bandied about for storage in sodium sulphur batteries. Not sure of the cost figures for SA wind, coal and gas. Then draw a horizontal line for the average monthly cost. If this exceeds say 15c per kwh wholesale price then it could be a cause for alarm.
The difference between wind output and demand could be the ‘gap’. Due to lags the gas ‘response’ curve would be somewhat right shifted. I don’t think it could ever fall to zero if steam units (closed and combined cycle) are involved. On a second graph show response vs demand gap. Excess response will add to storage and vice versa. Below that on the same time scale graph the storage level and rate showing upper and lower bounds. This will be particularly interesting eg if storage falls to zero.
Sorry if this sounds muddled.
Woah! The last few days of January don’t look real good at all. Even using all the storage we can and all the wind we can get, we’d still need all the gas we can get!
Moral of the story so far seems to be unless the cost of storage (which limits the size of the ‘bucket’) can come down 100 fold, fossil fuels are going to be required to back a renewable system up.
Hi John,
have you got a link on those costs? Because my understanding is that the capital cost of stored energy is so high that once one looks into storing electricity for any significant period of time – say around 2 days of serious grid storage – you may just as well spend the same amount of money on a nuclear power plant that would give you reliable power *all year* instead of now and then.
What a terrific abstraction! My inner engineer says it passes the bullshit test.
My inner businessman would want to find the optimal mix of “storage” and gas. One assumes in the real world we would optimise for cost as we have assumed that demand is always met. So we would then adjust the amount of storage (or gas) to deliver the lowest cost. Possibly on this basis if the storage is very expensive (eg batteries) the optimal might be zero storage.
If the “storage” is relatively inexpensive (as in inter-state links) then the use of gas would be minimised. On this basis you could use this model to calculate just how much gas back-up you actually do need for a given wind capacity. The storage pipes would be the link capacity in each direction and the “storage” size would be the limit of demand/supply the neighbour could accept. Just idle thoughts.
Barry,
I realise that you sort of look at open-blog science as an accessible alternative to journal publishing, and that this is just a starting point in a greater project, but are you going to try to get this published? It looks sound enough to me.
Tom Keen: Yes, it will definitely be written up and published in the peer-reviewed technical literature, once we think we have a sufficient package of coherent materials. At this point, however, consider this a first draft, open for refereeing by YOU (i.e. the community in general).
Martin: Agreed, and we are now doing some of this optimisation. An obvious first optimisation step is the storage/pipe trade-off that saves the most gas. We also need to consider ramp rates and peak demand smoothing, in later iterations, as well as the optimal mix between combined cycle and open cycle gas turbines (either of which can, in theory, also feed into the storage, along with the wind).
Francis thinks storage costs might not be a factor, if we consider the wind system to be a way of saving hydro (standard, not pumped) that would otherwise be used in the Snowys and Tassie.
Eclipsenow: If you are willing to build enough gas to equal peak (perhaps flattened peak) power demands, then you would never need anywhere near 2 days storage. You’d just burn more gas during those low wind periods. Right now, the system as configured is obviously very reliant on having gas around, and is about finding out how much gas is saved as wind penetration increases. To calculate this realistically, as a next step, we obviously also need to start to factor in the CCGT/OCGT mix, as mentioned above, and the amount of gas used in different ramping/spinning reserve scenarios. For now, it’s at a higher (more abstract) level than that.
The ever reliable Wikipedia seems reluctant to give cost comparisons of energy storage. The 10c/kwh for sodium sulphur was a throwaway line I remember from The Oil Drum. The difficulty must relate to the tradeoffs between unit capital cost (eg hydro dam vs flywheel), short working life such as batteries and poor round trip efficiencies such as reversible hydrogen fuel cells. However there are no gigawatt-hour scale chemical storage systems AFAIK.
An instantaneous cost function could assume output was steady in one hour increments. Thus open cycle gas could be weighted at say $100 and wind at say $80 per Mwh, using Wiki figures. As a numerical convention flow battery drawdown could be priced at say $100 per Mwh but charging up would have no assigned cost. Sample calculation 300 Mw wind, 1200 Mw gas and 200 Mw ex-storage would cost a weighted average of $96 per Mwh or 9.6c per kwh.
I think estimating cost of storage is important because I’m sure gas won’t last as long as we think when everybody is using it. Note Saudi Arabia is now thinking of importing LNG and Norway says its once boundless reserves will peak within a decade. This will happen to Australia within decades and the gas option will be extremely expensive.
Hi John,
here’s some rough costs of storage Barry helped me out with (I’m not very technical) based on the idea of storing power as heat in huge ‘gravel batteries’.
http://eclipsenow.wordpress.com/storing-energy/
A couple of measures may be useful in judging the FFS scheduling.
– Let GU = gas used with no Wind or Storage and AGU is actual gas used, so the ratio of AGU/GU should be as small as possible … we want to save fossil fuels.
– AGU/GU should also be a function of the ratio of InstalledWindCapacity/Average Demand. ie. how does the amount of
gas you can save vary as you overbuild wind capacity (or storage).
Lastly, some probability estimates would be good for how often actual demand will exceed available supply for given ratios of installed gas capacity/average demand and installed wind capacity/average demand.
And a question … We don’t want to waste
gas, but do we care about wasted wind? Do we really need to minimise this?
Depends on the pricing scheme. If the folks who paid for the wind turbines are selling output by the kWhr, then they’ll care about the wasted wind.
” I think estimating cost of storage is important because I’m sure gas won’t last as long as we think when everybody is using it. Note Saudi Arabia is now thinking of importing LNG and Norway says its once boundless reserves will peak within a decade. This will happen to Australia within decades and the gas option will be extremely expensive. ”
Indeed. Look at the problems faced by other countries in the world, using a similar approach as described in this great article. We basically have to NOT rely solely on wind turbines, we need a far more diversified RE supply, that needs to include solar and biomass and hydro. Of course what is the price tag of all that ? Of course what is the price tag of using coal or nuclear long term, given the externalized costs and internalized profits inherent of our sustainable societies ?
Not easy answers.
http://www.windpowermonthly.com/go/windalert/article/1006718/?DCMP=EMC-WindpowerWeekly
A sublime article about windpower in china and the mammoth technical issues they are facing. CHINA: Not everyone is upbeat about the future of Chinese wind. Miao Wei, vice-minister of the Ministry of Industry and Information Technology (MIIT), recently astonished listeners at the annual meeting of the National People’s Congress by declaring most of the country’s wind power plants “image projects” built by local authorities more for show than to meet energy demand. Miao was particularly irked by the huge wind base in Jiuquan City, in China’s north-western Gansu province. It is the country’s first 10GW-level wind project.
http://www.windpowermonthly.com/go/windalert/article/1006717/?DCMP=EMC-WindpowerWeekly
http://www.renewableenergyworld.com/rea/blog/post/2010/06/solar-photovoltaics-pv-is-cost-competitive-now?cmpid=SolarNL-Tuesday-June29-2010
Solar Photovoltaics (PV) is Cost-Competitive Now. So some nudnik from the oil or coal industries can stand up and say, PV is 40 c/kWh and not be lying. And I can say it is 13 c/kWh and not be lying, and all without a cent of incentives, not even traditional depreciation.
Sure John. I understand windmill owners aim to minimise time they aren’t being
paid … but is there a material cost associated with running a windmill
when the power isn’t being used? Does it substantially reduce the
life time? I know zip about these things.
just to follow the thread
Storage is complex, and will cost money – eventually.
At the -moment- we consider the ‘bucket’ storage to abstract three real and current types of storage: (i) Pumped Storage Hydro (PSH) of which the NEM has ~ 20 GWh, (ii) spatial smoothing of demand between the states, and perhaps some inkling of an idea that SA may be a net exporter of wind power, and (iii) the displacement of ‘pure’ hydro (of which we have a lot when dams are full) from times of lower value to times of higher value – the market can probably be expected to sort this one out.
Note always that systems change as their underpinnings change, and we can expect that as the wind penetration increases the use of cheap power will be taken up in various ways, and the misuse of expensive (scarce) power will decline. So long as there are no disruptions to supply and no great price hikes, this is all part of an evolutionary process that can be foreseen, but is hard to quantify, and harder still to quantify for every extra year one tries to look ahead.
responses over at OzEA please (feel free to cross post).
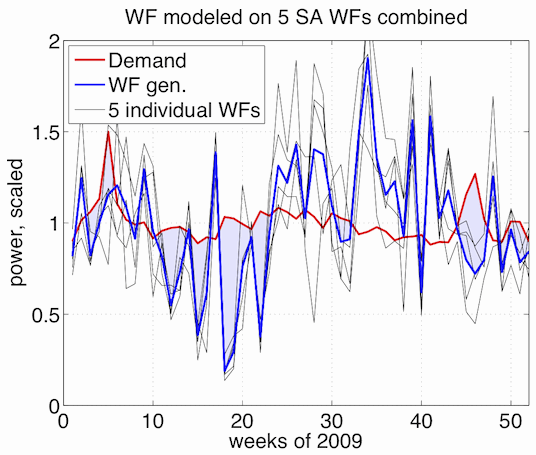
The “WF modeled on 5 SA WFs combined” figure presents a hypothetical situation, that South Australia wind turbine annual output has been scaled up 14.86-fold, without making it clear how very hypothetical this is.
I haven’t worked the five individual traces in, but the sum of the five, plus the demand, plus a thin grey trace representing the hypothetically upscaled five-windfarm output, I emailed yesterday (as we count time here). Why not put that up?
(How fire can be domesticated)
Thanks G.R.L. Cowan
I did get you mail, but have been out of action today. Happy to post (will do so shortly) but it was not immediately clear to me that this was your intention.
I’d be interested to hear if others share the concern with this representation?
I’ll also note than in the medium term the underlying data of this analysis will be updated to include more wind farms.
G.R.L. Cowan,
I got mugged by other stuff – will post your plot tomorrow – promise.
cheers -fc
It’s hard to reconcile the enormous range of estimates quoted for energy storage. Via Peak Energy the California Energy Commission suggests 3.8c per kwh. I seem to recall lead acid storage cost around 15c per kwh due to rapid degradation of the battery. The Peter Lang article on pumped hydro suggests tens of dollars per kwh. Barry B’s calculation on gravel heat storage doesn’t convert readily to cost per kwh but seems to be around the pumped hydro magnitude. I’d like to see a peer reviewed table of comparative costs.
Talking of comparisons the Chinese term ‘image project’ for uneconomic wind power contrasts with Lovelock’s term ‘gesture’.
This looks like a really good start to seeing what would be needed to replace most FF generated electricity with renewable. Unless we include solar in the mix we need to have more than 3GW of wind capacity(4.5GW) and more than 50GWh storage. Considerintg that TAS hydro alone has about 15,000GWh storage capacity 50GWh is a rediculously low amount. The cheapest storge at present is saving the use of existing hydro ( virtually no cost or losses). SA is presently limited to 500MW grid connections to this resource but this could be greatly expanded.
Barry, I am very happy to see this modeling being done, your modeling, so far, tracks closely to analysis I performed two years ago. I concluded then that wind + storage schemes, would be far more expensive than nuclear power while being far less reliable. I also concluded that my own limitations, particularly a lack of scientific and/or engineering training, precluded me from advancing the thread further, but I hoped that people who had the right training would pick up the problem and work it out properly. The OZ EA project is doing that.
Compare the plot at the top of this column with a little more information, log scale.
(How fire can be domesticated)
A satisfactory (technical term), but not necessarily optimal (technical term) to this problem can rapidly be found using simulated annealing on a so-called ANN (artifical nural network) which is the sechduling algorithm with inputs which include the storage level. The simulated annealing tries various combinations of parameters which set the “actions” of the ANN and rather rapidly rapidly settles down on a highly satifactory solution. There are many other machine learning algorithms which might work as well or better.
This way you don’t have to go on forwever and a day devising eer more clever “heuristic” control algorithms. Instead, entice some researchers in Omputer Science or Control Engineering to help you find satisfactory solutions which a “nearly” optimal.
Excellent, thanks GRL Cowan for that figure — it makes our assumption regarding the scaling up of current installations more explicit.
Our assumption is based on the reasoning that these 5 wind farms across SA have quite a wide geographic spread (Eyre Peninsula to the southeast), and so provide a reasonable approximation for a much larger scale up. However, the best available wind sites in SA, away from serious local objections, are all on the Eyre, so we might want to also consider a ‘sensitivity’ run where we take only Mt Millar and Cathedral rocks, and use these for the extra 2 GW of peak capacity, leaving the original (already installed) ~1 GW in place.
Charles, thanks — and note that your feedback on the current work, including any analyses you may wish to try, would be greatly appreciated over at OzEA.
Our assumption is based on the reasoning that these 5 wind farms across SA have quite a wide geographic spread (Eyre Peninsula to the southeast), and so provide a reasonable approximation for a much larger scale up.
Not a valid conclusion, you are ignoring the high variance of single sites and the size of weather systems that are larger than EP to SE. The SA state covers a much much larger geographical area than bounded by the 5 farms. It does provide a worse case scenario, so if renewable would work in SA based on this model it should work for all of Australia providing storage needs(approx 1000GWh) can be scaled up X15-20 fold. Luckly this seems possible.
I disagree that it’s a worse case scenario Neil, because future development WILL focus around certain key areas, such as the Eyre, which have good resources and are still relatively close to the main transmission infrastructure.
Neil, what do you mean about ignoring the high variance of single sites — could you clarify? It seems (correct me if I’m wrong) that you are arguing that our scale-up assumption is conservative in the sense that we may be overestimating the inter-farm correlation, whereas GRL Cowan is arguing (implicitly) that we may be underestimating it. In regards to your point Neil, there is a kind of test done already — the chart which includes the Vic and Tas wind farms too, and the situation compared to just the SA farms hasn’t changed much at all.
By the way, please also ask this question/make this point over at OzEA, so we can continue to conversation there.
Barry if I’ve understood this correctly the point of the exercise is to see if SA could go it alone with electricity supply and not rely on interstate imports. Looking at averages it appears demand will be 1 to 1.5 GW. However I recall AEMO saying that in heatwaves it approaches 3GW but the red line does not go this high in 2009. Nameplate wind in SA is around 800 MW I believe with an average output of around 300 MW, dropping to less than 100 MW in heatwaves. Scaling up 800 MW wind capacity to 2000 suggests the average will be (2000/800) X 300 = 750 MW. However the heatwave low wind output may still be very low if most wind farms are becalmed.
John, not quite, interstate imports/exports must always be part of the deal for SA. Although we’re starting with a highly abstracted system, we still want some reality and the interconnector ‘pipes’ provide that. Look at the blue sections in the final figures, these are the wind supply gaps that you mention.
That line you are looking at is hourly averages, and the maximum values are about 2.7 GW, see here . The 5 min peak might get as high as 3 GW, but I’d need to check.
Neil Howes,
You have mentioned several times that we have ample hydro storage to support wind power.
There may be a misunderstanding about what the existing hydro storage is for. The existing hydro storage is needed to store sufficient energy in wet periods (multi-decade time scale) to allow us to generate the hydro electricity we need through long dry periods.
Hydro is needed to provide rapid response to balance the fluctuation in the grid cause by normal and unusual demand fluctuations. It is also needed to provide large generation capacity for short periods when there is a disruption to a large power station.
Australia does not have sufficient hydro capacity to do this job as well as we would like. So why would we want to compromise the existing, minimal amount of hydro storage in attempting to try to make wind power seem viable?
Hydro generated just 12 TWh in 2007-08. Snowy Hydro’s capacity factor was just 14%. Should we divert that valuable resource to backing up for wind power?
Lake Eucumbene, the main storage reservoir, is currently at 20% full.
By the way, you have quoted the total amount of hydro energy storage available based on the full supply level of all the storage reservoirs. When calculating the amount of storage available we should use the minimum, not the maximum. This is because we need to be able to guarantee 95% availability to meet the contracts to supply the power when dispatched.
http://www.abare.gov.au/publications_html/energy/energy_10/ch_8.pdf
Barry,
Just for interest I’ve done a rough estimate of the capital cost of the infrastructure for the “20 GWh storage and 1GW pipes” option and compared it with a nuclear option.
Requirements for both options: 1.5 GW average power, 2 GW peak power.
Option 1 – Wind, Pumped-Hydro and Gas
Gas generation capacity: 1.5 GW @ $1,000/kW = $1.5 billion
Pumped hydro generating capacity: 1 GW @ $1,500/kW = $1.5 billion
Pumped hydro storage capacity: 20 GWh @ $150/kWh = $3 billion
Wind generating capacity: 3 GW @ $2,600/kW = $7.8 billion
Transmission extra costs: 3 GW @ $1,000/kW = $3 billion
Total capital cost = $16.8 billion
Option 2 – Nuclear and Pumped-Hydro
Nuclear: 1.5 GW @ $4000/kW = $6 billion
Pumped hydro generating capacity: 0.5 GW @ $1,500/kW = $0.75 billion
Pumped hydro storage capacity: 4 GWh @ $150/kWh = $0.6 billion
Total for the nuclear option = $7.35 billion.
Cost Comparison:
Option 1 – Wind, pumped-hydro & gas = $16.8 billion
Option 2 – Nuclear & pumped hydro = $7.35 billion
The nuclear option is less than half the cost of the renewables option.
This is very rough cost estimate. We could argue about details but, as you say, we might risk fixating on trees without taking time to appreciate the forest
Peter Lang, on 2 July 2010 at 19.53 — Seems to settle the matter. Thank you.
May I bring this modelling back to some practical reality. It is certainly interesting to consider how much gas and storage would be needed to support SA if it scaled the wind power 15 fold but this will never be done in reality.
There seems to be concensus in the wind literature that anything more than 40% penetration (by energy) is unlikely to add to wind capacity credit. In other words it isn’t worth doing – at least not from a network reliability point of view.
e.g. http://www.ieawind.org/AnnexXXV/Publications/W82.pdf
If we assume the other 60+% of demand is met with reliable supply the model basic equation will become:
Demand + DS + Spill = WFS + FFS + RS
Where RS means “reliable supply” which can be considered = Demand x 0.6
Simplifying the equation becomes:
Demand x 0.4 + DS +Spill = WFS + FFS
It would be interesting to see how DS and FFS change using this formula against the original model. Naturally WFS would need to be scaled down from the original model. I suspect this will be a much more realistic assessment than considering an “all wind + backup” solution.
Martin Nicholson.
I am just musing and wondering what is the break even point at which no more wind power is economic. My gut feeling is that wind power is not economic at any penetration if we had a truly ‘level playing field’ for generators – even with a very tight constraint on emisisons. This belief is supported by the “Emissions Cuts Realities” paper which suggests that wind power is not economic nor is it the least cost way to cut emissions at any level of penetration. A more refined analysis may show that wind power can reduce emissions cost effectively up to perhaps 1%, 3% or 5% penetration – perhaps.
I realise the modelling is in the very early stages of development and what is unusual about this exercise is the modelling group is exposing all their thoughts and development iterations to the pubic for constructive comments by some and ridicule by those who are that way inclined.
However, I’d like to encourage the modelling to have, as a long term aim, a chart which shows the costs of options including the breakeven point at which no more wind capacity is economic.
Figure 3 here http://bravenewclimate.files.wordpress.com/2009/08/peter-lang-wind-power.pdf shows the cost of electricity from coal, CCGT and OCGT as a function of Capacity factor for NSW in 2004. It shows the Capacity Factors at which one technology becomes more economic than another. I would like to see a figure that shows at what penetration wind power is economic for various generation mixes.
Gambler’s ruin in supplying power demand
I suppose the steady state demand is met by an NPP and CCGTs for the daily run up and then down. What I consider the tshort (15 minutes, say) random component of Demand occasioned by overtimes in World Cup games or whatnot. I assume these are meant by an random Supply (less predicatable that ev en wind). The is also a Bucket of capacity a which starts at level z.
At each unit of time Supply tosses a fair coin which comes up +1 or 0. At the same time Demand tosses another which comes up either -1 or 0. If Supply+Demand = 0, which happens half the time, then there is no change to the Bucket level and that round is a bye. Otherwise, the Bucket level goes up or down by 1. If the Bucket level reaches a, it can’t go higher and we say the gambler has won the game. If the Bucket level declines to zero, the gambler is ruined (to simplify). From quite classical probabilty theory, the probability of ruin is
q(z) = 1 – z/a
and the expected duration of the game (not counting byes) is
D(z) = z(a-z).
While there are more sophisticated analyses available which more accuratly treat what happens after winning, this is enough to see that intermittent supply eventually drains the bucket. What then?
David, electricity networks don’t quite work the same way as your gambler model – if I have understood your model correctly.
Supply + Demand = 0 has to happen ALL the time or at least close enough that the voltage or frequency doesn’t get out of the allowed (narrow) range of +/ – 1%. This means the network has to have the right amount of generating capacity to match the load moment by moment. The matching happens automatically of course through governors that control the “fuel” supply on the operating generators. It also happens on some demand response loads that can be wound up and down (or turned off).
Certainly the demand is somewhat random (at least at the margin) but it isn’t right to think of this “variable” supply as random at all. It is directly driven by the demand. Hence the probability of failure is very low – at least in a well managed network. Most of our blackouts these days are caused by the transmission/distribution system not by poor matching of demand and supply.
It’s only 15 times the 5 sample wind farms. Total peak capacity in SA has now (or will any day) hit 1 GW, and another 2 GW are on the cards, according to my inside sources. So the 3 GW peak scenario we’ve analysed here really is a realistic proposition — IF they can sort out the interstate transmission requirements (interconnectors — our ‘pipes’). In this respect it IS adding capacity credit, because Victoria currently has very little wind and is unlikely to be get much more in the short- to medium-term (again, according to my sources).
Thanks Barry. I should have checked SA energy demand before I jumped to the conclusion you were modelling an all wind scenario. However you are still probably looking at a greater than 50% penetration of wind within SA.
AEMO forecasts 15 TWh for 2010 for SA.
http://www.aemo.com.au/planning/0400-0013.pdf
3 GW of wind could generate about 8 TWh. This would be a penetration of over 50%.
I realise that with suitable sized pipes the network can be considered to be the whole NEM and so SA wind will be a smaller part of the total network.
In which case the modelling possible should be done using the total NEM demand.
Martin, that’s correct, look at the Figure M1-1 in the post above. It shows that with 3 GW peak, the penetration is about 50% for SA.
We certainly intend to model the whole NEM in later iterations — for now, it is simply treated as a ‘black box’, connected to SA via the pipes.
Martin Nicholson, on 3 July 2010 at 12.24 — The are two sources of supply. Random Supply and dispatchable Bucket. The are two sources of demand; random Demand and dispatachable Bucket. This is a simplified model of a pumped hydro facility supplied solely by something like wind.
No, its not etirely realistic, but enough to illustrate the problem of the Bucket becoming empty. So there has to be a dispatchable reserve capacity to (partly) refill the Bucket.
Which was the point.
When SA imports electricity from the eastern States that supply is vulnerable because their demand is high as well. I think it was in 2007 when a converter station on the Basslink cable overheated in an air temperature of 35C which nobody had planned for. Thus the ‘pipes’ may have to be assigned a probability of failure which increases with percentage of capacity.
A geographical oddity is that while the WA grid is not connected to the Eastern grid, SA sits on one side of the Big Coal States Qld, NSW and Vic. In a sense these States must ‘carry’ SA and Tas during shortfalls . There appear to be no plans to make SA a regular exporter of electricity.
Barry, I can see sense in just modelling SA to begin with to “hone” the model. Although I would encourage the use of a lower scale-up for wind in the model to closer to 30% of demand.
I would just be vary wary of jumping to any conclusions about the likely demand for storage or gas back-up from such a model because of the impact of the “black box” – which is probably closer to varying shades of grey.
science live! — new (draft) discussion for model one up and in need of wheel kicking.
Will make some comments in response to some posts above a little later.
David B. Benson, on 2 July 2010 at 8.45
Yes, at some point (when we are able to specify meaningful objective functions) I’m all for turning optimisation problems over to an ‘expert’; for now the heuristic wrangling is productive as we seek understanding.
Neil Howes, on 2 July 2010 at 10.47
Yes, we need to broaden our Wind Farm selection – this is in progress, although I doubt it will make much difference to the current work.
Peter Lang, on 2 July 2010 at 14.59
Yes, the level of the Dams over time is a critical consideration.
Peter Lang, on 2 July 2010 at 19.53
Sure, just for interest this is interesting, and since this is BNC (not OzEA) I can say I view the issues with nuclear power and climate change as far more complex than many others seem to. My reckoning is that what you or I think about these touchstone issues (from scientific or engineering or economic perspectives) is barely relevant; what matters is what society at large is doing, as expressed through political decisions.
As far as trees and forests, the problem spins both ways — it is my best guess and hope (and Barry’s too) that we have pitched the boundaries of OzEA in the most useful way we can.
David B. Benson, on 3 July 2010 at 7.57
What matter is settled? In what way?
Martin Nicholson, on 3 July 2010 at 8.42
Yes – absolutely. Some accounting of this form for the coal assets in SA (and elsewhere) will be necessary as we work the asymptote to reality.
John Newlands, on 4 July 2010 at 7.32
Yes – this aspect (high demand everywhere) will be treated explicitly in our modelling before we make any strong claims that might be undermined by this reality.
A clarification:
wrt my above comments in reference to: Peter Lang, on 2 July 2010 at 19.53
it seems I rushed to conclusion and didn’t properly comprehend what Peter was saying in relation to forests and trees. Ran into a tree. (-:
I’ve updated this post to include new, improved versions of figure M1-3. Click on the figures for a high res version.
We also now have a draft discussion posted. Please provides some feedback over at the OzEA page:
I don’t think that this should have been released here. I said in the comments of the OZWEA site that this is imagining 5 mega wind farms at the sites of the present ones and is not really valid.
You cannot possibly draw any conclusions from this part of the study. I was under the impression from Francis that this was a first attempt to get the modelling right.
I think that a huge caveat should be placed at the start of this post!
Does OZWEA stand for Oz Wind Energy Association?
Stephen compare the 5-SA-wind-farm output with the version based on wind farms spread across SA, Vic and Tas. They are not very different (…closer to almost indistinguishable). Then look at Figure 4 and you can again see very little difference to the 5-WF situation. Why then, do you you think the caveat is ‘huge’?
Also, statements such as “I don’t think that this should have been released here” are silly. The OzEA work is open science and a work in progress, and BNC is similarly open. No special claims were made about the work that would warrant censoring it at any particular stage in its development, like you seem to demand by this statement.
In my rough cost estimate here http://bravenewclimate.com/2010/06/30/ozea-bucket-wind-model/#comment-78094
I under-estimated the cost of Option 1 by $0.5 billion. The cost comparison shoud read:
Option 1 – Wind, pumped-hydro & gas = $17.3 billion
Option 2 – Nuclear & pumped hydro = $7.35 billion
I misread the amount of gas generation capacity needed. I allowed 1.5 GW but should have allowed 2 GW (see peak gas generation required on 28 Jan 2009 here http://www.oz-energy-analysis.org/models/model1_Bucket_Storage_and_Gas.php.
Barry Brook – “They are not very different ”
Not very different is not very scientific. They are actually very different.
I refer you to Francis’s reply to my objections to using only 5 wind farms:
“Subject: working depth into breadth
Date: 2010-06-08 (at 14:23:55)
Stephen, What I have not made clear here (and this will come out in the second story when I post it) is that the ‘game’ at the moment is to do layers of ‘breadth’, with no pretence whatsoever that this is anything but exploratory analysis. As we flesh out these layers (and I’m still working to complete layer one), we stand back and look at the places that are most important to refine the ‘depth’ on the next pass. I expect we will need a good few passes before we get down into some of these more detailed issues.”
This is only exploratory and should have such a caveat at the top of the post if you are going to post it here.
5 super sites means that variations in any one site greatly varies the final output and ignores the spatial smoothing of large numbers of wind sites that are geographically spread. Even if you add a few from Vic and Tas you still have the same problem.
Proper analysis will come from many sites when we can simulate some data. The correlation work I am doing at present I think will help to characterise datasets and simulate many wind farms with similar correlations and weibull parameters as good wind sites well seperated.
Only then can you unleash the costings. I am not advocating censoring just proper labelling of the analysis.
In what way? How did you quantify this, or at the very least plot this?
I don’t get it. What makes BNC any different to OzEA in this respect?
You seem to be arguing here that it will be microsite variation (i.e. inter-site white noise) that will create a large smoothing effect, rather than geographical separation (i.e. spatially structured red noise). Is this what you are saying? This is certainly counter to published work on this topic (e.g. Archer & Jacobson 2007, the new PNAS 2010 paper we refer to on the website), which argues strongly that geographic variation is the main determinant of spatial autocorrelation. Where is your evidence that is contrary to this ‘accepted wisdom’ that is backed up by a fair number of studies to date? Anyway, I do appreciate the correlation analysis you are doing and will be interested to see the results.
Woops,
Sorry all. I had the rough cost estimate correct the first time (here: http://bravenewclimate.com/2010/06/30/ozea-bucket-wind-model/#comment-78094). The peak power generated by gas is about 1.5GW on 28 January 2009 on the ‘Storage 2′ scenario (20GWh storage and 1 GW pipes). For my (incorrect) correcton I read 2 GW of gas power from the chart for ‘Storage 1′ (5GW storage and 0.5MW pipes). Sorry for the confusion.
On another matter, It would be interesting to compare the two alternatives on the basis of CO2 emissions. Very roughly, we could guess the emissions intensity (EI) for the wind + pumped hydro + gas option would be around 0.6 – 0.7 t/MWh. I am guessing the EI would be this high because:
1. Mostly OCGT would be needed to back up for the wind rather than CCGT. Even if the proportion is 50:50 OCGT and CCGT I would expect the emisions intensity to be similar to gas alone.
2. It is proposed to use gas generation for pumping. We can expect about 75% to 80% efficiency. So the emission intensity for the energy retreived from storage, that was pumped using gas turbines, will be 0.6/80% to 0.7/75% = 0.75 to 0.93 t/MWh. Almost as bad as coal!
Therefore, expect the wind + pumped hydro + gas option to have emissions intensity around 0.6 to 0.7 t/MWh.
For comparison, EI for the nuclear + pumped hydro option would have emissions intensity around 0.02 t/MWh.
Not only is the wind + pumped hydro + gas option about twice the cost, it also emits about 30 times as much CO2.
Very roughly, I calculate the emissions avoidance cost for the two options (in $/t CO2 avoided) to be:
Wind + pumped hydro + gas = $300/t CO2 avoided
Nuclear + pumped hydro = $40/t CO2 avoided
The more we look at the renewables options the worse they seem to be.
Francis, on 4 July 2010 at 19.13 — NPP+pumped hydro beats wind+gas+pumped hydro aout 3:1, according to Peter.
Oops.
2:1
Costing – I think Peter was right the 2nd time. The plots are normalised to average demand = 1.5 Gw = 1, so the peak demand is twice the average, peak gas usage is a bit over 2 GWe. From the storage 2 data file, the peak is 28th Jan, 1 pm, total demand 3269 Mw, gas 2137 Mw.
Unfortunately, the simple cost comparison is only relevant to building the system from scratch. As Barry said earlier, there is 1 Gw of wind already, and another 2 Gw almost certain to be built. Much of the gas is built too, so all of this is sunk cost. Given that, does upgrading the link to Tas to 1 Gw so that the water can be saved for peak demand as much as possible make sense as the best way to make use of what is / is going to be available, even though it isn’t what we would choose to build? So long as the average water usage over weekly time-scales is less than it would be with no wind and no upgraded link, the inter-annual averaging that the Tas reservoirs perform should not be effected.
Luke_UK, that’s correct. The peak in SA hits about 2.8 GW, so the end-January 2009 region would need 2 to 2.5 GW of gas capacity, depending on storage.
Francis’ view is very much aligned with what you’re saying about Tas hydro – there is a large potential resource there to be ‘saved’, if the interconnectors are of sufficient volume, even if there is no extra pumped-hydro storage installed. That’s the theory at least — something we plan to evaluate as the modelling develops further.
Luke and Barry,
Thank you for correcting me on the gas capcity and reading off the scaled graph. My mistake.
Regarding SA absconding with Tasmania’s hydro resource, I reckon the rest of the NEM might have a view on that. Any hydro resource is enormously valuable for balancing the NEM and for emergency use, so to use it for trying to make wind power viable seems like a dreadful wast to me. We’ll know more as the development of the modelling progresses.
I’d suspect that wind capacity installed in Tasmania would make more sense than in SA.
Also, I reitterate, that we cannot assume that the reservoirs are full. We need to be able to depend on always having the power available when needed, so we’d need to base the size of the resource on the minimum storage, not the maximum storage.
I agree it will be interesting to see where the modelling ends up when it is developed to the point of being able to compare the cost of the various options.
Barry Brook – “In what way? How did you quantify this, or at the very least plot this?”
In exactly the same way you did – I didn’t quantify it which is exactly my point.
OZEA is supposed to be an open science site where people understand preliminary studies are not to be taken for anything other what they are.
Sorry I do not know how to put my opinions of BNC politely as regard to renewables. I tried twice. I asked and received your assurance that OZEA was about the science of renewables. Releasing incomplete data about renewables on a nuclear advocate site like BNC is violating the the spirit behind that assurance.
If this is going to be the case in future then there is no way in the wide world I am going to post anything at OZEA.
“You seem to be arguing here that it will be microsite variation (i.e. inter-site white noise) that will create a large smoothing effect, rather than geographical separation (i.e. spatially structured red noise). ”
No I am not saying anything of the sort. Archer et al 2007 found that both the spatial distribution AND the number of wind farms made a difference.
“However,so long as more sites were added to a given array in such a way that the area covered became increasingly larger (as in the base case), statistical correlation among the sites decreased and so did standard deviations (Table2 and Fig. 4), thus improving array reliability and performance. Note that array-average wind speed and power may become lower for increasingly larger areas if sites in lower wind power class are added to the initial pool.”
For the 5 site case loss of wind at one site knocks out 1/5 of the generating capacity because so much capacity is concentrated in small area. this then produces the dramatic peaks and troughs of this scenerio. Such a large penetration if wind would never be done from such a small amount of sites no matter how well distributed they are. That is why this preliminary study is not valid to be used for costings or any other conclusion about wind power in SA. It is what it is – a preliminary study.
BTW I sent in the correlation analysis. It is very preliminary and incomplete as yet and may not be up to the standards of the site. I hope to get better data for WA soon (I have paid for it) so as soon as I do it will be posted along with the BOM data for the database.
Barry,
I would support Stephens comments, and add that the critical diffeerence will not be during low wind events, due to large high pressure sytems, but during high wind events due to smaller low pressure fronts moving rapidly across the state ( and SE of Australia)
The result is that a large number(50) farms over a reasonable geographical area(1million sq km) will have lower maximum capacity. This is critical as it allows much higher capacity to be built and a smaller storage pipe, probably about 1500MW assuming load shedding >50% off-peak and >70% peak. This means less OCGT back-up(1700MW) is needed and it can be used at much lower capacity, as the high demand spikes are rare and concentrated in later summer( when storage bucket is full). Older NG and coal fired could be on care and maintanence most of year, and only on standby when the bucket is empty.
ok, sticking my toe back in here… perhaps unwisely.
wrt Peter Lang’s costings, as I said before this is interesting, but no more. The idea that it settles anything seems silly to me (and I don’t take Peter as suggesting such).
wrt to the 5 Wind Farms, I am one with Barry here – I really don’t think it will make much difference, BUT I have and I do accept that we need to run the numbers – and we will. Always happy to have small bets on issues like this if they can be formulated.
In terms of the more general point about Barry posting OZEA material here and the nuclear / renewables / climate change issues / advocacy — it is never going to be simple. I say this to Stephen in particular – Barry and I have very different views on all these issues, but we share something much more important and powerful; we share a passion for science, we share first hand experience of how in practice science can be very messy and political, and we share a deep desire to be part of pioneering better and more open ways of doing science.
For me the second sentence of this BNC post (“The work presented here is high level and abstracted, and will be developed in future rounds.”) is sufficient caveat. Further, OzEA is an Open Science website that does not have a view on Nuclear Power — but Barry does have a view, and as far as I am concerned it is entirely ok for him to do what he wishes with OzEA material on HIS site.
On OzEA (“Our Site” – and this includes all who earn their strips there over time) we have some clearly spelt out rules. We (as OzEA) have NO PARTICULAR VIEW on the desirability of renewables or a particular renewable technology (especially in relation to a comparison with Nuclear — these comparisons, and ultimately decisions, are for society at large; we do not seek to tell society what to do). What we are doing is examining, to the best of our ability, what would be involved in achieving high renewable penetration. As we do this anyone can make whatever comparisons they like, BUT, not necessarily on the OzEA site.
http://www.oz-energy-analysis.org/rules.php
It would be interesting to see solar thermal added to the mix. A solar thermal plant in the North of the state would perhaps be counter cyclical to wind – i.e generate power on hot, still, high pressure days.
I assume also that peak power demand in South Australia is driven by air conditioning demand, which is highest on hot, still days? That would favour solar power.
The other factor in the future is that demand will become more elastic. Future houses will be well insulated with a good thermal store. That means the air-conditioning can run at night, or whenever the their is spare capacity. Same with electric cars.
Peter Lang
There may be a misunderstanding about what the existing hydro storage is for. The existing hydro storage is needed to store sufficient energy in wet periods (multi-decade time scale) to allow us to generate the hydro electricity we need through long dry periods.
At least for TAS, they are generating most of their daily electricity from hydro, and have surplus capacity to lend power for days or weeks or months as they have < one years storage and consume 8000GWh/year. For SA we are talking about 50GWh ( option3) ie just 2 days average power consumption by TAS.
Hydro is needed to provide rapid response to balance the fluctuation in the grid cause by normal and unusual demand fluctuations. It is also needed to provide large generation capacity for short periods when there is a disruption to a large power station.
If all SA’s present NG capacity is maintained we still have the same reserve capacity(but use at a much lower capacity), accommodating rare demand spikes uses very little water, overall hydro is running at about 20% capacity utilization(7GW/1.5GW av)
Neil Howes,
On point 1, where as designers of systems that are dominated by fossil fuel and nuclear generation are primarily concerned about “capacity”, designers of systems where hydro dominates are concerned with “energy”. That is, how they manage their energy over the long term. They need sufficient storage to see them through long (multi decadal periods of below average inflows. So, we would be unwise to take the enormously valuable hydro to use for firming wind in SA. I agree with using hydro storage to firm wind as long as we have a rule that we will not use any more hydro resource in excess of what the wind energy has stored or saved so far.
Why would we want to use our hydro resource to firm wind in SA when we need the high value hydro for the whole NEM? I’d rather use the hydro capacity and storage for what it is designed for and most valuable for. Also, if it is going to firm wind, I’d use it for firming wind in Tasmania where hydro is used for baseload generation.
However, I am sure all this will become obvious as the modelling gets to a more sophisticated level that it is now.
Peter,
I agree with using hydro storage to firm wind as long as we have a rule that we will not use any more hydro resource in excess of what the wind energy has stored or saved so far.
That is very reasonable and I would accept this rule. I would add that in periods when all hydro is being used for other applications NG back-up would have to be used, and when it is not possible to save hydro excess wind would have to be load shed. The exception would be a share of any purpose built pumped storage.
Neil Howes,
Wow! We’ve actually agreed on something.
My caveat of course, which goes without saying, is that I’d only support wind power if it is economic without subsidies. I can’t see how that can be the case, virtually ever.
Wind capacity costs about $2600/kW in Australia.
That is for a capacity factor of about 30%
Transmission extra cost: allow $1000/kW
Pumped hydro capacity: allow $1500/kW
Pumped hydro storage capacity: allow $150/kW
Pumped hydro efficiency: allow 75% when used with wind
NG back up capacity: allow $1000/kW
That is a lot of $/kW. It looks to be considerably more than $4,000/kW for nuclear. And higher operating cost too.
It also looks like it would produce a lot more GHG emissions than nuclear – given the need for NG back up at around 0.7 g/kWh of gas (that is what we could expect from NG used for backing up for wind power).
I really wonder why people believe so strongly in wind power.
Woops This line shoud be kWh not kW:
Pumped hydro storage: allow $150/kWh storage capacity.
Live comments feed now available on Oz-Energy-Analysis.ORG:
http://www.oz-energy-analysis.org/activity.php
Now, at last, it’s super easy to see who’s posting comments in which topics. This will be the first ‘port of call’ when you revisit the site. Each comment now also has a unique, web-linked identifier.
Compare the cost of wind power and nuclear power on the basis that they must be able to provide baseload power:
Requirements:
1. Power is available on demand whenever we demand it – every instant of every day and every night
Cost of nuclear power
Assumptions:
1. the first nuclear power station would cost the same or less than the first nuclear power station to be built in United Arab Republic (contract for four APR1400 units awarded to a Korean consortium a few months ago); i.e.
A$4,100/kW
2. The cost of further units would decrease over time, to say
$3,000/kW for the sixth unit
Cost of wind power (to provide reliable, on demand power)
$2,600/kW for the Wind farms.
$1,000/kW cost for transmission and grid enhancements to manage the peak and fluctating wind power
$1,000/kW for gas generators to provide the power when the wind is not blowing at full power
$4,600/kW total
But wind power delivers, on average, only about 1/3 the energy of a nuclear power station of the same capacity. So we need 3 wind farms to produce the same average power per year as a nuclear power station. So the cost of the wind farms to provide the same energy as a nuclear power station would be:
$7,800/kW of average power for the wind farms
$3,000/kW of average power for the transmission and grid upgrades
$1,000/kW for gas generation for backup when there is no wind
$11,800/kW total
An alternative to back up with gas generators is to use energy storage, such as pumped hydro, compressed air or batteries. Pumped hydro is the cheapest option where the appropriate topographic and geological conditions are available (Australia does not have much economic hydro potential near our major demand centres).
If we did have economic pumped hydro sites available the cost might be something like this:
$7,800/kW of average power for the wind farms
$3,000/kW of average power for the transmission and grid upgrades
$1,500/kW for pumped hydro generating capacity
$100/kWh for energy storage capacity and we’d need say 50 days energy storage to get us through periods of below average wind generation; 50d x 24h/d = 1200h @ $100/kWh =
$120,000/kW
$134,300/kW total
Is there a error in this last figure?
Peter your last calculation assumes new transmission, major dam modifications and additional generating capacity such as reversible turbine motors set in into the hillside. I suspect a no-frills version of the Canary Islands wind pumped system could be done a lot cheaper. For example the turbine hall in Tasmania’s Gordon Dam for example has vacant slots for two 142 MW Francis units. There is no downstream irrigation to worry about. If water was pumped back uphill from the spillway (augmented by a pond) the cost of external pumps could be moderate. Further savings could be made using unregulated power from nearby wind farms and variable speed electric motors on the pumps.
I’m not sure you need to treble the capital cost of wind. In a sense you are already converting it from say 25% capacity factor to 80% or whatever.
I question what is to be done long term about hydro if the rivers are gradually drying, not just here but in the US such as Hoover Dam. Wind electric pumping could be their salvation.
John Newlands,
You are thinking about adding a small incremental amount onto our existing system. Try thinking about a replacement for a substantial proportion of our coal fired generating capacity. The mistake you are making is common amongst those arguing for renewables. They expect others to subsidise renewables. Your points are an example of focusing on trees and missing the forest.
Wind Penetration by Installed Capacity has had a substantial clean up.
There has been some criticism of the limited data used here (5 SA Wind Farms), and the potential this has to under-account for spatial smoothing effects. With the Round Two data (when it is ready) we will examine the size of this problem. There is also a request (from Peter Lang in the comments below) to look not just at the hour-to-hour level, but to also consider this analysis in terms of the 5 minute Wind Farm data; this will also be part of the next Round here.
http://www.oz-energy-analysis.org/analysis/wind_penetration.php
I just saw this chart of electrcity generation by fuel type for UK for 13 July: http://www.bmreports.com/bsp/bsp_home.htm
Notice:
1. Wind generates most when least needed; ie in the low demand time. This causes more problems for the system
2. Minimal generation from hydro
3. Pumped hydro shows up to help out at peak, but contributes a tiny amount.
4. The real grunt is provided by coal, gas and nuclear.
5. UK is importing a lot more electricity from France than it is getting from its renewable energy generators.
This is the real world, folks.
[…] output will exceed demand, in which case the energy is dumped, or sold at negative cost. This “spilled wind” reduces the capacity factor, or impacts the economics of the generator. It means that beyond […]
Peter, that Electricity generation by fuel type chart says it all. Do you know of
any similar chart for Germany or Denmark?
Geoff Russell,
The charts for electricity generation by fuel type are available for each country here:
http://www.iea.org/stats/index.asp
This is the one for Germany:
http://www.iea.org/stats/pdf_graphs/DEELEC.pdf
Denmark:
http://www.iea.org/stats/pdf_graphs/DKELEC.pdf
France: I presume you have seen this site for France:
http://www.rte-france.com/fr/developpement-durable/maitriser-sa-consommation-electrique/consommation-production-et-contenu-co2-de-l-electricite-francaise
Move your mouse left and right across the power versus time area chart and notice changes in the pie chart below. Also note: virtually no wind power. Also notice, Frances very low CO2 emissions – in fact. France’s CO2 emissions from electricity generation (per MWh) are the lowest amongst the developed economies.
Comment on Denmark: In looking at the generation by fuel chart for Denmark it is important to recall that 75% of the wind energy is exported, then bought back when needed. It is exported at a very low price (because it is almost valueless) and bought back at premium price. The Danes are paying an enormous subsidy for their ideological obsession with renewable energy and with windmills.
Peter. Many thanks, but the links are missing.
Geoff,
Sorry for that. I’ve tried to reposts, and made several attempts but it is not accepting my post. I tried to just post the links but it is not accepting that either. They must be held up in the spam bank. Have to wait until Barry gets to it and clear out my several repeat attempts.
Curious … perhaps you just send them to [email protected] ? Thank Peter.
All fixed, I can see links now. Thanks.
Reasonable power from the NEM wind farms yesterday, except at the time of peak demand!!
http://windfarmperformance.info/
[…] OzEA modelling – large-scale wind power using a bucket storage model and gas backup […]
An article in New Scientist 30 March 2011 by Mark Buchanan, Magazine issue 2806, about a paper by Axel Kleidon of the Max Planck Institute for Biogeochemistry in Jena, Germany, says that efforts to satisfy a large proportion of our energy needs from the wind and waves will sap a significant proportion of the usable energy available from the sun. In effect, he says, we will be depleting green energy sources. His logic rests on the laws of thermodynamics, which point inescapably to the fact that only a fraction of the solar energy reaching Earth can be exploited to generate energy we can use.
Using a model of global circulation, Kleidon found that the amount of energy which we can expect to harness from the wind is reduced by a factor of 100 if you take into account the depletion of free energy by wind farms. It remains theoretically possible to extract up to 70 TW globally, but doing so would have serious consequences.
Although the winds will not die, sucking that much energy out of the atmosphere in Kleidon’s model changed precipitation, turbulence and the amount of solar radiation reaching the Earth’s surface. The magnitude of the changes was comparable to the changes to the climate caused by doubling atmospheric concentrations of carbon dioxide (Earth System Dynamics, DOI: 10.5194/esd-2-1-2011).