.png)
Guest Post by Peter Lang. Peter is a retired geologist and engineer with 40 years experience on a wide range of energy projects throughout the world, including managing energy R&D and providing policy advice for government and opposition. His experience includes: coal, oil, gas, hydro, geothermal, nuclear power plants, nuclear waste disposal, and a wide range of energy end use management projects.
A 10-page printable PDF version of this post can be downloaded here.
An Excel worksheet showing the calculations (allowing you to change inputs/assumptions) is also available.
Introduction
What is the cost of carbon dioxide (CO2) emissions abatement with the various electricity generation technologies being considered for Australia?
The abatement cost of a technology depends on many factors such as the engineering characteristics of the electricity grid to which the new technology will be connected, the geographic location and many others. One important factor often not mentioned is the reference case against which the abatement cost is calculated. The abatement cost for a new technology is only meaningful when compared with another new technology or with an existing generator it would ‘displace’; e.g. nuclear compared with a new coal power station or nuclear compared with an existing power station.
The Electric Power Research Institute (EPRI, 2010) report http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf for the Australian Department of Resources, Energy and Tourism provides data that allows CO2 abatement costs to be estimated for a range of new technologies. Unfortunately, the report is complex and opaque in parts.
The purpose of this paper is twofold:
- to summarise in tabular form the relevant information from the EPRI report so others can access it easily and produce levelised cost of electricity (LCOE) figures under differing assumptions, particularly using the NREL LCOE calculator http://www.nrel.gov/analysis/tech_lcoe.html .
- to calculate and compare the CO2 abatement costs for a range of new technologies for each of three ‘displaced’ technologies.
This paper does not attempt to calculate the effects of carbon price on the LCOE or CO2 abatement costs, because:
1) the EPRI report does not include the effects of carbon price — nor feed in tariffs, renewable energy certificates and other subsidies — so incorporating the effect of CO2 pricing, and other incentives and disincentives in the analysis would require many additional assumptions, and
2) the purpose of this paper is to show the abatement costs for the various technologies so options can be compared and so the cost of incentives and disincentives (including carbon pricing), which would be needed to make each technology viable, can be made visible.
Methodology
The CO2 abatement cost is calculated for seven new electricity generation technologies, selected from the EPRI report. The seven new technologies are:
- Coal (black, without CCS).
- Coal (black, with CCS)
- Nuclear
- CCGT (Combined Cycle Gas Turbine)
- OCGT (Open Cycle Gas Turbine)
- Wind (wind class 5, 100 x 2 MW)
- Solar thermal (Central Receiver, 6h storage, DNI = 6)
The abatement cost for each is calculated by comparison with each of three ‘displaced’ technologies:
- Hazelwood, brown coal power station, Victoria (1,600 MW, commissioned 1964 to 1971)
- Liddell (see photo above), black coal power station, NSW (2,000 MW, commissioned 1971 to 1973)
- A new black coal plant, withoutCCS; (this is same as #1 in the list of new technologies).
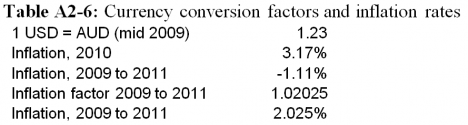
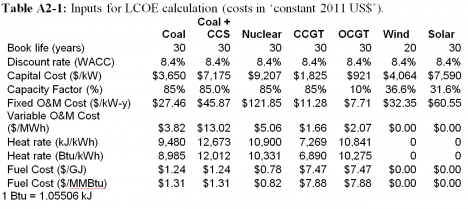
Most input data are taken from EPRI (2010) http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf ; these are summarised in Appendix 1. To bring the figures up to date and to aid in international comparisons, costs presented in Table 1 have been converted from 2009 A$ to 2011 US$; these are in Appendix 2. Details of the costings, including the exchange rates and inflation rates used, are included. The calculation steps and results are presented.
CO2 Abatement Cost is the difference in LCOE divided by the difference in CO2 emission intensity (EI):
CO2 abatement Cost = (LCOEnew – LCOEdisplaced) / (EIdisplaced – EInew)
The data needed for calculating LCOE for each technology, using the NREL simplified LCOE calculator http://www.nrel.gov/analysis/tech_lcoe.html, are provided in the Appendices.
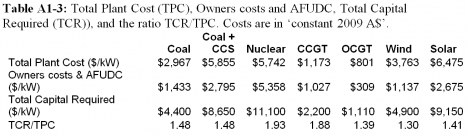
The capital cost is one of the inputs needed for the LCOE calculation. The capital cost figure needed is the Total Capital Required (TCR). But theTCRfigure is not given in the EPRI report. As such, the method of estimating it, including the inputs and intermediate calculation results, are presented in Appendix 1.
The CO2 emissions intensity (EI) presented in the EPRI report includes only the emissions from burning the fuel in the generator. Fugitive emissions are not included. Nor do the emissions intensities include the higher emissions intensities produced when load-following; e.g. when cycling power up and down to back-up for intermittent renewable energy generators.
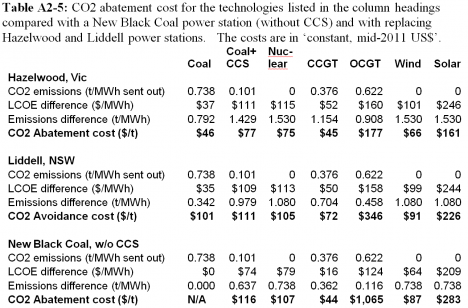
The emissions intensities (EI) for Liddell and Hazelwood power stations are 1.08 t/MWh and 1.53 t/MWh (sent out) respectively (ACIL-Tasman (2009), Table 18 http://www.aemo.com.au/planning/419-0035.pdf ). These EIs include fugitive emissions (whereas the EPRI EIs do not). This causes an error in the calculated abatement costs. In the ACIL Tasman report, fugitive emissions comprise 10% to 27% of EI for gas, 2% to 9% for black coal and 0.3% for brown coal.
The LCOE for Liddell and Hazelwood are ‘Commercial in Confidence’, so I’ve used $30 and $28 respectively, which are figures I’ve seen stated for the ‘equivalent LCOE’ for the remaining plant life.
Results
The CO2 abatement costs are summarised in Figure 1.
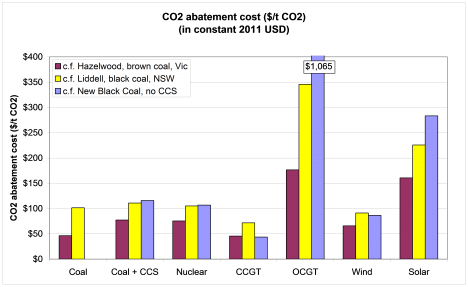Figure 1: CO2 abatement cost for seven selected new technologies (named on the horizontal axis) compared with each of three ‘displaced’ technologies (named in the legend). Abatement costs are in US$/tonne CO2 (constant, 2011US$).
The inputs and intermediate calculation results are in Appendix 1 (in 2009 A$) and Appendix 2 (in 2011 US$). The data in Figure 1 is from Table A2-5.
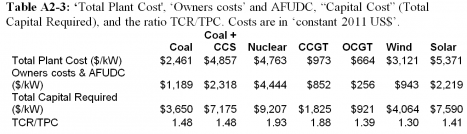
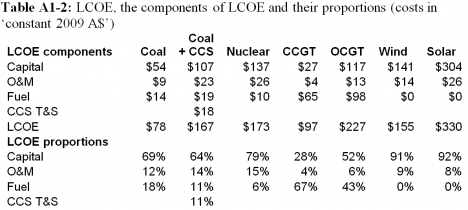
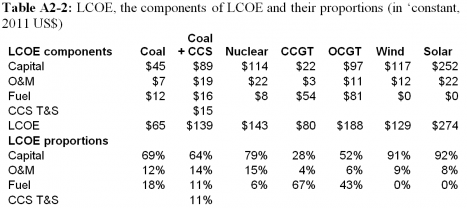
Table A1-2 and A2-2 show the proportion of “Capital” (i.e. TCR) that EPRI apparently assumed for ‘Owners Costs’, including ‘Allowance for Funds Used During Construction’ (AFUDC).
The ratio TCR/TPC is given in Tables A1-3 and A2-3. This ratio shows how much higher the TCR is than TPC for each technology. For example, for nuclear the TCR is 1.93, or 93% greater than TPC.
Discussion
This report uses the EPRI (2010) figures for LCOE and emissions intensity. These are the figures being used in Australian government reports such as ABARE (2010) and for the Treasury modelling of the carbon tax and ETS. Some discussion of the figures and assumptions is warranted.
The Total Plant Cost figure in the EPRI report is confusing because it is not the full capital cost used to calculate LCOE. The capital cost figure needed for calculating LCOE is the Total Capital Required, which includes Owner’s Costs. Back-calculating from the figures provided reveals the amount of Owner’s Costs EPRI used in their LCOE analyses. This cost is significant. It is 93% higher than the Total Plant Cost for nuclear, 88% higher for CCGT, 45% higher for coal, and 41% higher for solar thermal. The EPRI report does not make clear the basis of the Owner’s Costs or the assumptions. For example, the construction period is not stated?
EPRI uses 85% for the average lifetime capacity factor for mature technologies such as coal, gas and nuclear. However it also uses 85% for immature technologies such as carbon capture and storage, and assumes capacity factors for Wind (36.6%) and Solar Thermal (31.6% with 6 hours storage) that appear to be based on the best possible figures, rather than the average achievable over a plant’s life. It is difficult to understand how these capacity factors could be realized in practice over the plant life.
The emissions intensities do not include fugitive emissions and appear to be for the technology running at optimum efficiency, rather than average efficiency. The abatement costs for Wind and Solar are probably understated, because the capacity factors assumed seem to be unreasonably high.
The reason the OCGT abatement costs are high is because EPRI used a capacity factor of 10% for the calculation of LCOE. This is because OCGT is economic at capacity factors up to about 14% due to its high fuel costs (IPART, 2004, Exhibits 1-2 and 1-3 http://www.ipart.nsw.gov.au/documents/Pubvers_Rev_Reg_Ret_IES010304.pdf )
If we assume wind or solar are backed up with OCGT, it is clear, without needing to do detailed calculations, that wind and solar with back-up are a high-cost way to avoid emissions.
Of the options considered, CCGT is clearly the least cost way to abate CO2 emissions. For example, if we are making a decision about new baseload capacity we might compare between a new baseload coal plant withoutCCSand other options. From Figure 1, the CO2 abatement cost, compared with new black coal, is $44/t CO2 for CCGT and $107/t CO2 for nuclear.
Based on the EPRI figures, nuclear cannot be justified inAustraliaat this time because it is too expensive. For nuclear to be an economically viable option, the impediments that are causing the EPRI estimates for the cost of nuclear in Australia to be several times higher than in Korea need to be removed.
Conclusions
Of the options considered, CCGT is clearly the least cost way to abate CO2 emissions, given the EPRI assumptions.
The abatement cost with CCGT is about 40% of the abatement cost with nuclear.
Based on EPRI’s estimates, nuclear is not economically viable in Australia because it is too expensive. This situation will remain while the impediments to low-cost nuclear remain in place.
Glossary
OCGT – Open Cycle Gas Turbine
CCGT – Combined Cycle Gas Turbine
CCS – Carbon Capture and Sequestration
CST – Concentrating Solar Thermal
EPRI – Electric Power Research Institute
NREL – National Renewable Energy Laboratory
LCOE – Levelised Cost of Electricity
TCR – Total Capital Required
TPC – Total Plant Cost
AFUDC – Accumulated [or Allowance for] Funds Used During Construction (Capitalised Interest)
References
ABARE (2010), Australian Energy Projections to 2029-30: http://adl.brs.gov.au/data/warehouse/pe_abarebrs99014434/energy_proj.pdf
ACIL-Tasman (2009), Fuel resource, new entry and generation costs in the NEM: http://www.aemo.com.au/planning/419-0035.pdf
EPRI (2010), Australian Electricity Generation Technology Costs – Reference Case 2010: http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf
Independent Pricing and Regulatory Tribunal (2004) The long run marginal cost of electricity generation in NSW: http://www.ipart.nsw.gov.au/documents/Pubvers_Rev_Reg_Ret_IES010304.pdf
NREL (2011), Levelized Cost of Energy Calculator: http://www.nrel.gov/analysis/tech_lcoe.html
South CarolinaElectric & Gas Company (2011), VC Summers Nuclear Station Units 2 and 3 (June 30, 2011): http://www.scana.com/NR/rdonlyres/A830A131-9425-46F1-B948-C8424530EE49/0/2011Q2BLRAReport.pdf
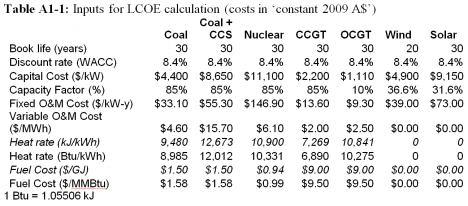
Appendix 1 – Input data and intermediate calculation results with costs in ‘constant 2009 A$’
Appendix 1 summarises the significant data from the EPRI (2010) report for the seven technologies selected for this study. Costs are in ‘constant, mid-2009 A$’.
Table A1-1 lists the values needed for input to the NREL LCOE Calculator, http://www.nrel.gov/analysis/tech_lcoe.html .
The Capital Cost figure listed in Table A1-1, needed for calculating LCOE, is ‘Total Capital Required’ (TCR). But the TCR figure is not given in the EPRI report. So it must be back-calculated from the other data available in the report. The EPRI report provides the breakdown of LCOE by Capital, O&M and Fuel (Tables A1-2 and A2-2). This data was used to calculate the value EPRI used for TCR. The results are in Tables A1-3 and A2-3. These tables also give the ratio TCR/TPC. This shows how much higher the TCR is than TPC for each technology. For example, for nuclear the TCR is 1.93, or 93% greater than TPC, whereas for coal it is 48%.
Appendix 2 – Input data and intermediate calculation results with costs in ‘constant 2011 US$’
The cost figures in Appendix 1 are in ‘constant, mid-2009 A$’. In Appendix 2 they have been converted to ‘constant, mid-2011 U$’. The conversion factors are in Table A2-6.
Table A2-1 lists the values needed for input to the NREL LCOE Calculator.
Filed under: Emissions, Nuclear, Policy, Renewables
These studies are meaningless because CCS fails a simple legal test. Utilities do not want to be held responsible for causing water table damage through litigation or even just the threat of litigation could bankrupt a power company. Recently President Obama (being a lawyer) was advised that the US should not provide guarantees holding owners of CCS not responsible for environmental damage by their projects. Therefore CCS fails an important test right off the bat. The above cost comparisons are meaningless because the technology cannot move forward legally. That leaves only the nuclear option which has its own set of risks that may be viewed as too risky or may be viewed as being managable depending on who you talk to. I personally think the risks can be minimized and are managable. The risk of our extinction by not developing nuclear power is huge and far outweighs the nuclear accident risk. Taking these points into account shows that coal is dead and nuclear has a necessary future. Solar is a toy we can play with – if you can afford it. Wind is too erratic to be the major source of energy in our overall power supply.
Following
1)This is interesting and I agree that it would be desirable to understand what adds to the cost of nuclear in many countries. Regulatory regimes are certainly very different and looking at NRC, for example, you get the feeling that they see their primary duty to be an obstacle for the construction of new NPPs in US rather than as a facilitator of (more) safe nuclear power.
2)The assumed gas prices seemed rather conservative and in a world where half the planet thinks gas is a cheap and easy way to lower CO2 emissions and where oil production might be peaking, I think the assumed prices can be reasonably questioned.
3)Finally, while I think this type of estimates have their own uses they also have serious shortcomings since they fail to ask whether to choosen alternative actually gets the job done. Emissions reductions we get from using gas (even when ignoring methane leakage) are too small by far. Also, CCS doesn’t capture all the CO2 and what is left can quite easily be intolerable if we are to reach the kind of reductions IPCC talks about (…let alone more aggressive 350ppm goals). In the end the cost comparisons that are most meaningful with climate change in mind, are those between alternative energy infrastructures that do get the job done rather than between those getting us, for example, 30% closer to the target but leaving the underlying problem unsolved.
Jani, you said “let alone more aggressive 350ppm goals”. 350 ppm is history. We are nearly at 400 ppm and going up. Stopping all CO2 release doesn’t get us back to a lower CO2 level since the total is cumulative. I sometimes wonder if a lot of people (350.org and our political leaders) think that dropping the CO2 production level also drops the total ppm level. If they think this, they just dont understand the cumulative nature of the total CO2 level. Because of this cumulative effect, all forms of CO2 production need to be eliminated as soon as possible. This concept is not yet in the mental psyche of people around the world. By the way I agree with all your points Jani.
Gene, I haven’t followed 350ppm movement very closely, but my understading has been that they want to eventually see forest cover increasing again. This would tie down co2 from the atmosphere.
How fast would planting trees lower the CO2? I have a gut feeling that planting trees is not going to have much effect except over millenia.
This is from WAAAYYY out in left field but…you know….if we returned the entire state of Nebraska and Iowa back to Prairie (the Prairie of the American Great Plains were super rich, dense forms of vegetation. Grasses with extensive root systems, where the carbon is deposited) we could drain the atmosphere of CO2 back to 1900 levels. Just say’n 🙂
I have attempted to find the average lifespan of Natural Gas fired turbines. My research, and i by no means maintain that it is comprehensive, suggests that it falls from 50,000 to 65,000 operational hours. Or at maximum, after about 8 years of continuous use the turbine must be replaced. 9 years if we assume a 90% capacity factor of nuclear power plants.
The cost distortions that have been omitted are not trivial. CO2 will cost $23/t from next July rising to about $29 in 2015. After that the auctioned price could go higher or lower but with a floor of $15 if I recall. The Renewable Energy Certificate subsidy will average $39 per Mwh this year and should be added as a cost to wind and solar.
Other cost factors can go either way such as the exchange rate. Since nobody knows if CCS is viable cost estimates would gave to be suspect. Note that some favoured projects such as the ‘solar flagships’ will get 45% of their capital costs paid by the Federal govt with no interest or dividend payments required. Of particular importance to southern Australia will be the gas price. If nearby gas sources have to be replaced by distant sources current prices paid could double.
Cost of CO2 avoided may be a short term and not a long term decision criterion. US power company Exelon claims that gas is cheaper than new nuclear and even in carbon taxed Australia TRU Energy appears to favour gas for new projects. Is this gas lock-in a wise move for the future?
The analysis is obviously nonsense because you are mitigating coal CO2 with coal. The cost of mitigating with nuclear cannot be as high as mitigating with coal because burning coal is not mitigating at all.
What we have to do to mitigate is to shut down coal and natural gas, not switch from coal to coal. Switching from coal to coal should show an infinite cost of mitigation.
There is an obvious misrepresentation in the cost of nuclear because nuclear is the cheapest and only way to actually mitigate.
Jani, on your point 3, I think this is key.
If you are concerned with mitigating climate change rather than just CO2, then gas-fired power stations are not the right technology. This is because the difference between the reduced positive CO2 forcing [from fossil gas combustion and methane leakage] and the diminished negative aerosol forcing is roughly zero [see Wigley analysis], whereas for nuclear there is also the diminished aerosol forcing (like gas), but NOT a positive CO2 or methane forcing, hence the net effect is still a substantial negative forcing. Looking to the bottom line, it is the negative forcing that matters for climate change.
Also, on CCS, we state in our Energy paper (Nicholson et al 2011):
Gene Preston @ 2 November 2011 at 10:41 PM
I agree with your comments about CCS. However, this is just one of the seven new technologies considered, so I don’t understand how you can dismiss the other six comparisons as your first sentence says:
By the way, I added the “Black Coal with CCS” technology as an after-thought. I added it because of comments a few days ago which argued that any comparison with coal should be for coal with CCS.
Jani Martikainen, @ 3 November 2011 at 12:48 AM:
Thank you. This is the only comment so far that seems to have made an attempt to understand the paper and to get to grips with the reality – nuclear is too expensive to be viable at the moment.
The fuel price assumptions are directly from the EPRI report. The EPRI report explains that is a large difference between west coast (high) and east coast (low) gas prices. They explain that it is not valid to average them, but since this is a study for Australia responding to the Australian Government’s terms of reference, that is what they did. I’d urge anyone who wants to argue about the EPRI assumptions to read the EPRI report first.
That is a different issue. This paper is intended to compare some selected technologies, being advocated for Australia, on the basis of their cost of electricity and the cost of emissions abatement. We need to do this as a first step, before we apply incentives and disincentives, so we can see how large the incentives and disincentives would have to be to make each technology viable. This analysis shows that CCGT is the least cost way to reduce emissions at this point in time. If we want nuclear, we’d better start looking into what is making it too expensive.
Charles Barton @ 3 November 2011 at 4:09 AM
The ‘book life’ for LCOE is usually taken to be 30 years in most of the studies I’ve seen. It is the period over which the capital cost is depreciated.
Please read the EPRI report to understand the EPRI assumptions.
John Newlands @ 3 November 2011 at 5:51 AM
The CO2 tax and ETS legislation will most likely be repealed (in the opinion of many). It cannot survive in a world that is not heading to implement an international ETS, which it is not. But the CO2 tax and ETS is OT for this thread.
Asteroid Miner @ 3 November 2011 at 7:32 AM
You comment suggests you did not read the paper very carefully.
Asteroid Miner, on 3 November 2011 at 7:32 AM said:
The analysis is obviously nonsense because you are mitigating coal CO2 with coal
You are mitigating a 1970′s sub critical coal fired plant with a 2010 super or ultra super critical coal fired plant. 25-28% efficiency vs 38% or 45% efficiency. It might not be as much a reduction in emissions as some would like but it would still represent a reduction.
@Gene Preston and others
James Hansen estimates that a maximal global reforestation effort would reduce atmospheric CO2 by about 50 ppm.
http://www.giss.nasa.gov/research/briefs/hansen_13/
That combined with very aggressive emissions cuts might make 350 ppm possible. Unfortunately, reality is somewhat different.
Following.
Thanks Peter for this clear and well-argued analysis of a complex subject.
Let’s revisit the nuclear cost question again. I checked the EPRI report and found no mention of the Korean APR1400. Since the UAE deal for four reactors was signed in 2009, I wonder why the APR1400 was not included. The UAE deal was for four 1,400 MWe reactors at $20 billion (mostly fixed cost!). That gives 5.6 GWe divided by 20 billion US dollars for a cost per kW of $3570 or 25% less than used by EPRI.
Can someone verify that I am comparing apples to apples?
Are there cultural reasons Australians can not buy from Asians?
Thanks for pulling this information together Peter.
The costs calculated in the analysis should be understood as the cost to remove the first tonne of CO2 emissions from the system. Lets not lose sight of our goal though: what is the cost of removing the last tonne of CO2 emissions from the system?
This cost is infinite for CCGT, OCGT, and black coal, because these technologies are simply not capable. It converges (perhaps diverges) towards a very large number for wind & solar, much larger than the EPRI cost used here.
Likewise coal + CCS appears to approach an arbitrarily large number as soon as we try to implement it – witness the closure of the UK’s last CCS scheme at Longannet in the same week as the closure of the only serious Australian CCS venture, Zerogen in QLD.
So for removal of the last tonne of emissions, rather than currently being more expensive, nuclear power is already the cheapest way to abate emissions from existing plant.
The ultimate value of any piece of analysis is, how does it inform or change any decision that we can make today? We could be making a decision today to build nuclear power. But we can only choose today to be building nuclear power in, say, 2020, because of the engineering and policy lead times. The choice between displacing Hazelwood with either nuclear or CCGT at today’s gas prices does not lie within our possible futures. The only choice that we get to make today is between displacing Hazelwood with either nuclear, or CCGT at 2020 fuel prices. And similarly for the other displacement options. And I’m prepared to accept John Newlands argument that gas will be much more expensive in 2020 than today.
(Call it the Special Theory of Political Relativity if you like – we can only make choices between events that could occur beyond a political implementation horizon that recedes from us at the speed of decision making.)
So even for removal of the first tonne of emissions, Peter’s analysis shows that it is highly likely that nuclear power is already the cheapest displacement choice we can make today.
We don’t need to make nuclear power cheaper, its already the cheapest available choice, today, for displacement of both the first and the last tonne of CO2 emissions.
Solid analysis, the justifications behind inputs and assumptions look fair, after a quick gloss over them.
I have to agree with points by Jani Martikainen, Barry Brook and John Morgain, i.e. the need to mitigate climate change, not just the cost of removing the first tonne of CO2. It does seem a little pointless estimating the abatement cost of replacing coal without ccs with more efficient coal without ccs (why bother?).
I note that the EPRI report states “Overall EPRI anticipates the capital cost of a nuclear power plant deployed in 2030 will be 15% less than one built in 2015.” (I can’t find their justification for this figure?)
If you play around with the excel inputs to accomodate for this assumed decrease in capital cost (85% of $US114 = $US97), it changes the resulting LCOE from US$143 to US$126, which changes the CO2 abatement cost at Liddell (where abatement cost is highest) from US$105/t to US$89/t. I wonder if this is a fair estimate for the cost of (what John Morgan referred to as) removing the last tonne of CO2 from the system?
By the looks of these results, Hazelwood is certainly a first contender to be replaced (and rightfully so).
[…] Brave New Climate: CO2 abatement cost with electricity generation options in Australia. […]
Martin Burkle,
Thank you for your comments and questions.
The EPRI report explains how they have estimated the cost for nuclear power in Australia. I’d urge BNCers to read and comprehend that if there aregument is with the EPRI estimates. However, I’d remide all that the EPRI figures are the ones htat have been commissioned by the Australian government and are being used in their modelling and analyses. So it is unlikely we will find a major flaw in them Therefore, I’d suggest it is best to work with the numbers currently available. Anyone wants to test different assumptions can download the Excel spreadsheet, vary the assumptions and see the effect.
I believe the figure for capital cost of the UAE project and the EPRI ‘Total Capital Required” are equivalent figures. So yes, you are comparing apples with apples on that basis. But there appears to be many factors which would make nuclear far more expensive than in UAE, and more expensive than in USA. One of them is that Australian labour productivity is lower and labour rates are higher than in USA. According to EPRI the uplift factor is 1.73, so the labour costs for the Australian component would be 73% higher in Australia than in USA. See the EPRI report for the details and the breakdown.
There are no legislated “cultural reasons Australians can not buy from Asia”. But I suspect, there is a strong view at present Australia should align its nuclear regulation with the USA nuclear regulatory regime. I believe doing so would cause Australia to commit to high cost nuclear for many decades.
Peter, Thanks for this analysis – at least it gives me a reason why the Govt keeps saying nuclear is too expensive, but I do admit that I don’t understand why “owner’s cost” for a nuclear plant should be 93% greater than the establishment cost in Aus which is several times higher than in Korea. Is this due to insurance? I would like to see how the Northern Power Station at Port Augusta in my home state compares. I have heard it is even dirtier than Hazelwood. It has a power output of 520-544MW and emits 3.6 million tonnes of greenhouse gas a year. I have been expecting that Alinta will replace it with an Open Cycle natural gas turbine plant using Moomba gas. Of course it is not a bad location for our first nuclear plant, producing desal water for the Roxby mine.
Re solar, I have always been skeptical of it as a large scale power source since I experienced first hand the White Cliffs 50kW Solar Power station in the late 1980s. It was more often down and using diesel backup than operating. Maybe solar is more reliable these days.
John Patterson
Peter Lang: WRONG: “nuclear is too expensive to be viable at the moment”
“Power to Save the World; The Truth About Nuclear Energy” by Gwyneth Cravens, 2007:
Page 211: “In 2005, the production cost of electricity from nuclear power on average cost 1.72 cents per kilowatt-hour; from coal-fired plants 2.21; from natural gas 7.5, and from oil 8.09. American nuclear power reactors operated that year around the clock at about 90 percent capacity, whereas coal-fired plants operated at about 73 percent, hydroelectric plants at 29 percent, natural gas from 16 to 38 percent, wind at 27 percent, solar at 19 percent, and geothermal at 75 percent.” The costs per kilowatt hour for solar and wind are 600 or more times the cost for coal, and that is in sunny and windy places, respectively.
Asteroid Miner @ 3 November 2011 at 7:32 AM
The analysis is obviously nonsense because you are mitigating coal CO2 with coal.
You comment suggests you did not read the paper very carefully.
So you would cure morphine addiction with heroin? It is as obvoius as the emperor’s new clothes that you can’t eliminate CO2 production by burning coal. Also from Cravens:
Page 13 has a chart of greenhouse gas emissions from electricity production. Nuclear power produces less greenhouse gas [CO2] than any other source, including coal, natural gas, hydro, solar and wind. Building wind turbines and towers also involve industrial processes such as concrete and steel making.
Wind turbines produce a total of 58 grams of CO2 per kilowatt hour.
Nuclear power plants produce a total of 30 grams of CO2 per kilowatt hour, the lowest.
Coal plants produce the most, between 966 and 1306 grams of CO2 per kilowatt hour.
Solar power produces between 100 and 280 grams of CO2 per kilowatt hour.
Hydro power produces 240 grams of CO2 per kilowatt hour.
Natural gas produces between 439 and 688 grams of CO2 per kilowatt hour.
(Deleted inflammatory remark.)
harrywr2, on 3 November 2011 at 8:11 AM: “25-28% efficiency vs 38% or 45% efficiency. It might not be as much a reduction in emissions as some would like but it would still represent a reduction.”
That much reduction would be irrelevant. We are already into dangerous territory. We are above 350 ppm and above 450 ppm equivalent, with CH4 bubbling out of the Arctic ocean and CH4 bubbling out of the peat bogs thawing in the tundra.
If we don’t act immediately and take draconian action, we humans could be extinct by 2060. This is not a joke.
Please read: http://onlinelibrary.wiley.com/doi/10.1002/wcc.81/full
“Drought Under Global Warming: a Review”
See the maps of drought in the 2060s on page 15.
http://www.realclimate.org/index.php/archives/2011/10/the-moscow-warming-hole/
http://thinkprogress.org/romm/2011/10/26/353997/nature-dust-bowlification-food-insecurity
http://www.pnas.org/content/early/2011/10/18/1101766108.abstract
http://www.sciencemag.org/content/early/2011/03/16/science.1201224
http://www.fas.org/irp/agency/dod/jason/statistics.pdf
http://climateprogress.org/2010/10/20/ncar-daidrought-under-global-warming-a-review/
http://climateprogress.org/2010/12/14/southwest-drought-global-warmin/
http://climateprogress.org/2011/01/20/lester-brown-extreme-weather-climate-change-record-food-prices/
“Preliminary Analysis of a Global Drought Time Series” by Barton Paul Levenson, not yet published. Under BAU [Business As Usual], agriculture and civilization will collapse some time between 2050 and 2055 due to drought caused by GW [Global Warming].
See:
“Ecological Footprints and Bio-Capacity: Essential Elements in Sustainability Assessment” by William E. Rees, PhD, University of British Columbia and “Living Planet Report 2008″ also by Rees.
We went past the Earth’s permanent carrying capacity for humans some time in the 1980s. We are 20%+ over our limit already. And the US no longer has excess biocapacity. We are feeding on imports. 4 Billion people will die because we are 2 Billion over the carrying capacity. An overshoot must be followed by an undershoot.
Reference: “The Long Summer” by Brian Fagan and “Collapse” by Jared Diamond. When agriculture collapses, civilization collapses. Fagan and Diamond told the stories of something like 2 dozen previous very small civilizations. Most of the collapses were caused by fraction of a degree climate changes. In some cases, all of that group died. On the average, 1 out of 10,000 survived. We humans could go EXTINCT in 2051. The 1 out of 10,000 survived because he wandered in the direction of food. If the collapse is global, there is no right direction.
1. We must take extreme action now. Cut CO2 production 40% by the end of 2015. [How to do this: Replace all coal fired power plants with factory built nuclear and renewables.] Continuing to make CO2 is the greatest imaginable GENOCIDE. We have to act NOW. Acting in 2049 will not work. Nature just doesn’t work that way. All fossil fuel fired power plants must be shut down and replaced with nuclear and renewables. Target date: 2015.
2. Expect at least 4 Billion people to die because of the population overshoot. Attempt to maintain some form of civilization while this happens.
How are we feeding 7 billion now? On “mined” water. Aquifers are running dry. When the aquifers are dry, the food is gone.
For small factory built nuclear power reactors see:
http://www.world-nuclear.org/info/inf33.html
Notice that several are made in the USA.
Small Nuclear Power Reactors
Name Capacity Type Developer
KLT-40S 35 MWe PWR OKBM, Russia
VK-300 300 MWe BWR Atomenergoproekt, Russia
CAREM 27 MWe PWR CNEA & INVAP, Argentina
IRIS 100-335 MWe PWR Westinghouse-led, international
Westinghouse SMR 200 MWe PWR Westinghouse, USA
mPower 125 MWe PWR Babcock & Wilcox, USA
SMART 100 MWe PWR KAERI, South Korea
NuScale 45 MWe PWR NuScale Power, USA
HTR-PM 2×105 MWe HTR INET & Huaneng, China
PBMR 80 MWe HTR Eskom, South Africa
GT-MHR 285 MWe HTR General Atomics (USA), Rosatom (Russia)
BREST 300 MWe FNR RDIPE, Russia
SVBR-100 100 MWe FNR Rosatom/En+, Russia
Hyperion PM 25 MWe FNR Hyperion, USA
Prism 311 MWe FNR GE-Hitachi, USA
FUJI 100 MWe MSR ITHMSO, Japan-Russia-USA
Hyperion from Arizona, USA has quoted me a retail cost of 5.5 cents per kilowatt hour. http://www.hyperionpowergeneration.com/
================
For Advanced Nuclear Power Reactors see:
http://www.world-nuclear.org/info/inf08.html
Third-generation reactors have:
a standardised design for each type to expedite licensing, reduce capital cost and reduce construction time,
The US Nuclear Regulatory Commission (NRC) gave final design certification for both in May 1997, noting that they exceeded NRC \”safety goals by several orders of magnitude\”.
The Westinghouse AP600 gained NRC final design certification in 1999 (AP = Advanced Passive).
These NRC approvals were the first such generic certifications to be issued and are valid for 15 years. As a result of an exhaustive public process, safety issues within the scope of the certified designs have been fully resolved and hence will not be open to legal challenge during licensing for particular plants. US utilities will be able to obtain a single NRC licence to both construct and operate a reactor before construction begins. etc.
See: http://www.realclimate.org/index.php/archives/2011/11/keystone-xl-game-over/
“Keystone XL: Game over?”
Do you understand what “Game over” means?
John Morgan, 3 November 2011 at 10:10 AM
Thank you for your comment. This response has got a bit long and convoluted, but I’ll post it anyway. I know you will get to the substance of it. 🙂
I disagree with your statement of the goal. The goal of this paper is to compare the abatement costs of different technologies. That is the sort of decision being made about CCGT to replace Hazelwood and new coal or CCGT for NSW. The analysis uses the best currently available information, which was provided by EPRI and which is the basis for the government’s analyses.
You have stated a system wide goal. That is not what this paper focuses on. However, as an aside, I think your statement of the system goal is not correct. The system goal is “what is the discounted cost of removing, not the last tonne but the <average tonne, of CO2 emissions from the system”. On a discounted cost basis the cost of removing the first tonnes is the most important.
Removing the last tonne is at least 40 years away. At that time the inputs to the analysis will be different. Right now, we must make the decision between options on the basis of which option will give the least LCOE and least abatement cost for the life of the next plant to be built.
I disagree. Consider the process for making a decision at some time in the future. The process will be the same as now. The decision will be which plant to build. If existing plants such as Hazelwood or Liddell still exist, the analysis will be the same. If we are making a decision about adding new capacity, the abatement cost analysis will still be the same analysis.
I agree that purchase decisions must be made now on the best estimate of LCOE (and therefore of fuel prices) for the life of the plant. Most analyses take into account the forecast cost of fuel over the projection period, as does the ACIL-Tasman report (see Section 4.2 and Tables 44 and 48: http://www.aemo.com.au/planning/419-0035.pdf ). Also remember there has been a significant decline in US gas prices over the past few years (due to coal seam gas), and similar may happen in Australia. So gas price forecasts are uncertain. Debating that assumption is another issue.
I agree.
It is clear nuclear is not economically viable in Australia at the moment, and will not be by 2020 unless we remove the impediments to low-cost nuclear. Most people doing the calculation are concluding just that. So if we want nuclear to be a realistic option, we need to investigate what needs to be done to allow it to be economic.
This is basically an argument about the projected gas price assumptions for 2020 and for the plant life. I agree that if we change EPRI’s assumptions it will change the results. EPRI conducted sensitivity analyses on capital, O&M, and Fuel costs for all technologies. They are presented in Section 10 http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf . I will run an analysis with different inputs and report later.
John, I am surprised by that statement. I cannot see evidence to support it. I am open to be persuaded so I hope you will present the case.
Asteroid Miner, you are preaching to the converted when it comes to SMRs. However, you might want to dampen your enthusiasm for them at this stage until there are some prototypes and commercial units built.
The only solid buyers that I’ve heard of recently are TVA, who are building some B&W mPower units. Hyperion hasn’t built a prototype yet and has no solid customers or NRC design approval.
There’s also the Akademik Lomonosov floating plant, but that’s up in the air at the moment.
The AP600 had no buyers and based on feedback from existing nuclear power customers they increased the output to 1150MW.
All of this reflects the current trends in nuclear power: China is driving development in high output (1GW+), evolved LWR designs and on the other hand there is a focus on SMRs in terms of R&D effort.
We’ll need both but if the climate threat is as serious as you suggest then we will need to build off-the-shelf Gen III reactor designs right now and get to building fast breeder prototypes to consume their spent fuel fast, perhaps as SMRs. France did a decent build-out of large nuclear power plants and if the climate problem was treated with the urgency it deserves then full electricity-sector decarbonisation could be achieved within <15 years in countries with existing nuclear regulatory frameworks.
LFTRs will be irrelevant for 5+ years unless there is a Manhattan Project-style crash program to develop and mass-produce them. This isn’tr to say that it’s impossible (I’m watching Flibe Energy’s work with the US Army as close as I can) but unless there a tectonic shift in politics then it probably won’t happen very fast at all.
As for:
"So you would cure morphine addiction with heroin? It is as obvoius as the emperor’s new clothes that you can’t eliminate CO2 production by burning coal."
It’s pretty obvious that you still haven’t read the paper. Emissions reduction can be done by using more efficient coal-powered generators – however, the deep cuts in emissions intensity for baseload power supply will require nuclear power in order to keep CO2 levels at current levels.
John Morgan @ 3 November 2011 at 10:10 AM
The EPRI report gives the projected costs in 2015 and 2030. the costs are in ‘Constant, 2009 A$’. Therefore, referring to 2020 prices could be confusing. What I understand you and John Newlands to mean is that you expect a real cost increase in gas prices – that is an increase above inflation. I am not sure what figure you have in mind for the price in 2020 (given in 2009 A$). I have run an analysis with gas at $12/GJ (constant, 2009 A$), which is the upper end of the range used in the EPRI sensitivity analyses for 2015. At this gas price and with no other changes CCGT still has the lowest CO2 abatement cost of the low emission technologies.
@Peter Lang “You have stated a system wide goal. That is not what this paper focuses on. However, as an aside, I think your statement of the system goal is not correct. The system goal is “what is the discounted cost of removing, not the last tonne but the <average tonne, of CO2 emissions from the system”. On a discounted cost basis the cost of removing the first tonnes is the most important.
Removing the last tonne is at least 40 years away. At that time the inputs to the analysis will be different. Right now, we must make the decision between options on the basis of which option will give the least LCOE and least abatement cost for the life of the next plant to be built."
I see your point, but the trouble I have with this is that it seems to assume that you find the decarbonized solution by always, at each moment of time, picking the lowest abatement cost alternative. The picture I have in mind is "energy landscape" with different technologies on different axis and the CO2 emission along the last axis..i..e CO2(tech1, tech2, tech3…). I see the danger that by following locally optimal steps, we end up in a local minimum of CO2 (with too high emissions) and not the global one that we must reach. Then making a jump from that one to the final solution could end up costlier than it should be. I am not being very clear right now, but I hope you see what I am trying to grasp.
Also, decisions we make today influence future costs. For example, first of a kind nuclear costs are higher and sooner we start learning faster the costs are lowered. Considering that in the case of nuclear costs that you quote are already fairly close to fossil alternatives it is not unreasonable to expect modest cost reduction which will make it the cheapest alternative. Paying a bit extra now, could get us moving into the direction of the global minimum. So as a picture, think we are on a mountain top. One side has a steep slope right away, but end ups only into a valley half way down hill. The other side starts with somewhat less steep slope, but the slope gets steeper and the route actually ends up all the way downhill. If we pick the first choice, there is the danger (danger not certainty) that we must eventually climb back up again to get where we wanted to get.
Thanks for your comments Peter. I understand where you’ve drawn the scope of your analysis. When I say our goal is to remove the last tonne of carbon emissions, I realize thats beyond the scope you’ve set yourself, but offer it to set what I think is the broader context in which these discussions reside. Let me expand on the comments of mine you disagree with.
We can’t remove the last tonne by replacement with OCGT or CCGT. I don’t believe it can be done with coal + CCS, since we don’t seem capable of removing a first tonne with this tech. I don’t believe it can be done with wind or solar, because the diminishing return as those technologies increase penetration will hit an integration wall long before the last tonne drops. That leaves nuclear as the only capable technology for final decarbonization, and so by exhaustion the cheapest.
I make the assumption here that gas prices will be significantly more expensive in a decade. That can be questioned, but it is the basis for my statement. My assumption is that the cost increase will offset the difference that separates nuclear from OCGT at current fuel prices. Since the choice we can make today is between a nuclear plant in, say, a decade, with a sixty year plant life, and OCGT in, say, a year with a thirty year plant life (I’ve no idea what typical life is), we need to consider gas cost 10, 20, 30 years out. I think gas will be much more expensive then even if it is still cheap in 2020.
So for today’s choice, even for the first tonne of carbon, I still think nuclear is likely to prove the cheapest available abatement technology.
Jani Martikainen, @ 3 November 2011 at 7:29 PM
Thank you for your comment
I think I understand what you are getting at. I agree with what I think you saying.
If I’ve understood you correctly, our agendas have similarities. In short this is mine:
To cut world emissions most of the effort has to be in the developing countries because they are the ones that will ramp up energy use as Japan did after WWII, followed by China, India, Indonesia and others. The rest of the developing world will go through this development cycle too. So what the developed world does in cutting its emissions is less important than providing low emission, electricity generation technologies for the developing world at a cost less than fossil fuel technologies. Therefore, our role should be focused on developing the technology. In the short term it means implementing Gen II and Gen III at the lowest possible cost. Australia should be aiming for an LCOE as near to Korea’s as is achievable. To achieve that means removing the impediments to low-cost nuclear.
The main aim of the lead article was to try to encourage BNC regulars to recognise and accept that nuclear is too expensive to be viable in Australia at the moment. We need to focus our attention on how to overcome that.
We also need to get over the idea that the CO2 tax and ETS is any sort of solution at all. It will not survive and even if it did it is not a solution because it does not help to get low cost nuclear. It protects it from the full magnitude of the cost reduction that is needed. That will not help to get it cheaper than coal, quickly.
I agree that the faster we get rolling out nuclear the faster costs will come down. We need to address the politics and educate the population. We also need to stop “kicking own goals” like the CO2 tax. That legislation has set back progress in Australia by at least 5 years IMO.
Regarding your last paragraph, I wonder if you have seen the section in this comment titled Nuclear cheaper than coal in Australia. How?
http://bravenewclimate.com/2011/07/06/carbon-tax-australia-2011/#comment-136436
I believe this is saying similar to what you are advocating in your last paragraph. It suggests what needs to be done to get to n’th of a kind cheaper than call. It provides rough costs and the total public funding needed for the first 10 GW.
John Morgan,
Thank you again. I’ll ponder on your comment overnight. Here is my initial reaction:
I agree with all of that up until the last four words: “ so by exhaustion the cheapest.”. The least cost solution will be the one that gives the least total cost on a discounted cash flow basis over the entire period. The least cost solution will be to build the plants that abate emissions at least cost first. Being pragmatic, we will need fossil fuel generation for a long time, much longer than the life of the initial plants. From another perspective, the political reality is either we go the least cost route or don’t do anything. The population is not likely to support nuclear if there is a lower cost solution available. Therefore, it seems clear to me, the choices are:
1. keep using coal until nuclear is cheaper
2. go gas, or
3. face up to the facts: nuclear is priced to high because of the impediments we (society) has caused our governments to place on it. Therefore, we can remove those impediments. The first step needs to be to identify the impediments.
Regarding your second point and the assumption about gas prices, most LCOE analyses are based on projected fuel prices for the plant life. I don’t recall what the EPRI report assumed, and they may not have made it explicit, but the assumptions are explicit, detailed, and based on specific Australian east coast information in the ACIL Tasman (2009) report, Section 4.2 http://www.aemo.com.au/planning/419-0035.pdf
@Peter: Thanks for you comment and I agree with what you say. At some moral level I would like to see carbon taxes, but I don’t see anyway for that to happen without the system leaking massively so that it doesn’t actually achieve anything other than higher energy costs and weakening public interest in emission reductions. Only convincing long term solution is zero carbon energy source that really is cheaper than fossil fuels. It is possible with nuclear, but it requires appropriate regulatory and political superstructure. There certainly can be (and are) systems where nuclear is not the cheapest choice. Investors on NPPs must be certain that their investment is welcome and regulations should be such that they encourage the evolution of reactor designs towards breeders.
I have little sympathy towards those who seem happy to let the energy prices go through the roof. I do not think they actually know how much industrialized countries spend on energy and that this spending pretty much makes everything else possible. If they would know this, they would also very quickly notice how crazy priorities they are making. I think here in Finland goverment spends less on health care (as a fraction of GDP) than we pay for energy. We pay somewhat more on pensions, and by 2030 that share is set to rise by about 3% to about 15% of GDP. This is widely considered a huge societal challenge, but the kind of energy cost increases some greens nonchalantly have in mind imply massively larger challenges. By the time people actually have to prioritize they will (and of course they should) choose the issues of direct relevance to their well being rather than ideologically kosher voltage differences.
I am wondering how yet another calculator exists with CCGT at an 85% capacity factor. I attempted to use the spreadsheet as a calculator, and after some of the posts here (particularly Jani Martikainen’s at 7:29 on the 3rd), I feel I should try this again.
What CCGT plant operates anywhere near 85% capacity factors (CF)?. The US EIA data shows they operate at closer to 40% levels there – http://www.eia.gov/cneaf/electricity/epa/epat5p2.html. Yet the same US EIA provides estimated levelized costs based on on 87% CFs, and that gets copied around the world. I find it ludicrous.
Adjusting only the CF for CCGT, by changing the LCOE’s capital component by 85/40, nuclear and CCGT become essentially the same costs as solutions for abating CO2 emissions, while CCGT remains a more attractive option in terms of $/MWh.
That covers the reasons it is getting built. It is more flexible than baseload and utilized primarily as the intermediate supply that comes on to match the day’s demand and goes away for the night’s low demand.
I couldn’t work out how the capital component of LCOE was being populated in the spreadsheet, and need to move on the more pressing matters now, but I’ll return to reality in the hopes more talented folks than I can model it.
There is a system supply requirement that comes from peak demand. If a portion of that supply (coal) is being removed, you need to measure how to replace it. Wind has a capacity value of under 10% many places (I saw 3% reference on this site for an Australian location) — so if you choose wind as the replacement you must also choose a source with the capacity value to actually replace the coal. If the CF of wind is 36.6%, then the CF of it’s complementary peaking source cannot be above 63.4%. Right?
So the calculator needs to be a matrix, where one change impacts another, both for level of supply, and CF.
I suspect the cheapest option for an entire system (that lacks hydro) is nuclear set at the level of minimum demand, and CCGT set to match the remainder of winter peak. Simplifying some figures from my Canadian province, 10GW of nuclear and 10GW of CCGT would be in the right ballpark. Average demand is about 16GW, so even in this scenario CCGT would only have a 60% CF. In fact in my area summer peak is higher, and I assume that could be met with solar – but that would reduce the overall CF of CCGT once again.
The ideal matrix here would then recognize the reality Germany has experienced. If you add wind, on a must take all output basis (which you’d have to for a high CF), that must reduce either the nuclear CF or, more likely, nuclear supply – meaning more CCGT.
The CO2 abatement cost is negative in that case.
Which we know is true.
I suspect the best way to get the cost of nuclear down is to get the motivation for expanding nuclear up. A more realistic evaluation of supposed alternatives might be helpful.
From the EPRI report, “An overall weighted Crew Rate Factor was calculated to be approximately 1.71, which is higher
than anticipated. ”
I’m in the United States and worry that the United States can not build nuclear due to the millions of hours required and the labor cost. To think that the labor component would be 1.71 times more than in the US is really hard for me to believe. Can someone explain whether this difference is due mainly to higher wages or being less skilled in the use of construction tools?
Is there anyplace to read about how labor is managed and paid in Korea or China as compared to the US or France?
Martin Burkle, on 4 November 2011 at 2:51 AM said:
Can someone explain whether this difference is due mainly to higher wages or being less skilled in the use of construction tools?
Workplace compensation rules…Australian’s have rules like if you aren’t given lunch break between noon and 1 pm then you are paid double-time until you get your lunch-break. They also get allowances for traveling to the job site, tools etc etc etc.
http://www.commerce.wa.gov.au/labourrelations/PDF/Awards/B/BuildingTradesConstructionAward.pdf
Building nuclear power plants involve lots of concrete. Stopping a continuous pour between noon and 1 pm everyday so everyone can go have lunch isn’t practical.
US Iron workers rates from http://www.bls.gov/oco/ocos215.htm
“In May 2008, median hourly wages of structural iron and steel workers were $20.68. The middle 50 percent earned between $15.18 and $29.15. The lowest 10 percent earned less than $12.25, and the highest 10 percent earned more than $37.04.
In May 2008, median hourly wages of reinforcing iron and rebar workers were $19.18. The middle 50 percent earned between $14.35 and $27.29. The lowest 10 percent earned less than $11.78, and the highest 10 percent earned more than $35.26.”
These hourly rates are about the same as the Australian hourly rates. My currency converter says $20 US is the same as 19.60 Ausy. So I conclude that the basic labor rates are the same in the US and in Australia.
Do you really think that Australian work rules add 70% to the cost of labor? That would be $20 an hour for work and $14 an hour for rules over and above the work rules in the US. If that’s the way it works, how do you expect to build any kind of serious energy infrastructure?
Martin Burkle, on 4 November 2011 at 6:04 AM said:
Do you really think that Australian work rules add 70% to the cost of labor?
Table 4-1 list productivity factors for steel work.
http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf
The Australian’s are better then Americans in terms of productivity on ‘fabricated steel’ as you get into lighter steel pieces Australian productivity drops to half.
I would speculate some sort of ‘lifting rule’ must be the explanation as the ‘fabricated heavy’ steel would be all crane work and the lighter pieces would involve people lifting something.
Since Australian’s are better at setting prefabricated pieces into place then a design that will be cost efficient for them has to have a higher prefabrication percentage.
(Deleted OT comments)
The conversion from coal to nuclear is the easiest conversion to make because we already have the technology. From coal to nuclear is also the biggest single wedge. The only problem is that the public has been propagandized by the coal industry into fearing all things nuclear. That can be cured with education.
MODERATOR
Some of your comment has been deleted as it is off topic on this thread.It is also a violation of BNC Comments Policy to make personal remarks or attribute motives to another commenter. BNC accepts the scientific consensus for AGW/CC
and no longer discusses or posts climate denialism. It is, therefore, not necessary for you to repeat the accepted BNC premise and is unfair to other commenters who, due to the new policy, have no right of reply.
Jani Martikainen, @ 3 November 2011 at 10:26 PM
Thank you for your comment.
We agree that the CO2 tax and ETS is no solution. In fact it will have the opposite of the desired effect.
I recognise that some people argue for a CO2e price on moral grounds. However, I’d argue it is highly immoral. There is no benefit but it would damage economies and, therefore, human wellbeing. So it is immoral.
Why there is no benefit: It won’t reduce world emissions, can’t work, and won’t be implemented http://bravenewclimate.com/2011/07/06/carbon-tax-australia-2011/#comment-140631 . It can’t work internationally. We can’t even measure CO2 emissions well enough to trade it in USA, EU or Australia. So what chance is there of measuring the emissions in Eretria or Ethiopia or anywhere? Therefore, there will be no international trading scheme. Most people have realised this by now e.g. A few are still hanging on.
I agree. Therefore, that is where we should be focusing our attention. We will not get nuclear seriously considered, let alone implemented, in Australia while LCOE of nuclear is far higher than with CCGT and the abatement cost per tonne is far higher than with CCGT.
If we want to seriously consider nuclear in Australia we need to:
• Identify all the impediments to low-cost nuclear in Australia, and all the energy market distortions
• Identify which could be removed
• Prioritise them for removal
• Define policy options for removing them
• Define what else would be needed to get nuclear through to the “settled down costs” (in Australia) stage
But before we can begin to tackle this,we need to get acceptance, especially from nuclear proponents, that nuclear is not an ecomically viable option for Australia at the moment. Therefore, it will not be given serious consideration. Worse still, IMO the CO2 tax and ETS legislation has delayed nuclear being put back on the political agenda for at least 5 years (unless the Labor dumps its anti-nuke policy at National Convention in December).
I agree totally with your last paragraph. I would add that the reason nuclear in Australia would be such high cost is because of 50 years of accumulated government interventions in the energy market (here and in other western democracies). We need to look afresh at all of this. Start looking at it from the perspective of a clean sheet of paper.
In summary,
Step one: recognise and accept the fact that nuclear is not a viable option for Australia at the moment.
Step two, identify the impediments to low cost nuclear in Australia.
It would also help if we could stop being distracted by advocating for the CO2 tax and ETS.
MODERATOR
Peter – your answer to JM is veering off topic and into the Carbon Tax discussion area. Please keep to the appropriate thread and do not use remarks on other threads to re-iterate your already widely espoused views on this matter. Further instances will be deleted.
Scott Luft, @ 4 November 2011 at 12:56 AM
Thank you for your comment. You make some good points, however …
Scott, and all readers, can I plead with you to read the EPRI report if you want to argue about the assumptions they used and their justification. Based on the reports I’ve seen over the past 30 years which compare LCOE of baseload technologies, nearly all use a common capacity factor to facilitate comparison. Then you can change inputs to see the effect of different assumptions.
The EPRI (2010) report applies a capacity factor of 10% for OCGT which is realistic because OCGT is used for peaking. However, the ACIL Tasman (2009) report uses a capacity factor of 85% for all technologies, including OCGT, to facilitate comparison despite the fact OCGT would not be dispatched to operate at 85% CF.
It is standard practice to apply consistent factors across the technologies to minimise the number of variables. If we did not do that, we would find nuclear has a higher LCOE because the discount rate would be higher for nuclear (higher financial risk therefore higher cost of money) than for CCGT.
OK. The spreadsheet is not well documented. You need to use the NREL LCOE calculator to calculate the LCOE. The spreadsheet is not doing that calculation. You must enter the LCOE in row 33.
Regarding the matrix you suggest, the answer is yes of course. But that requires sophisticated system wide modelling capability. We can’t do that on simple spreadsheets and post it in articles here. That is done by groups with huge resources, and a lot of consideration about boundary conditions and inputs. The key point of this paper is to try to get readers here to understand why it is generally accepted that nuclear is not economically viable in Australia at the moment. Once people accept that, we can move on to investigating what is making it too expensive and what would need to be done to allow it to be economically viable.
Funny you should mention that. I knew some one would say something along the lines. So burried a little surprise in the spreadsheet. Unhide columns L, M N. (hide column K to avoid confusion). This calculates the LCOE and CO2 abatement cost for 30% wind and 55% OCGT (total 85% capacity factor so the results are comparable with the other baseload technologies). The LCOE for 30% wind and 55% OCGT is $109/MWh (in 2011 US$). The abatement cost is $132/tonne. (I think this is correct, but haven’t checked it carefully).
No. That is not the case while nuclear is more expensive than coal. Our current system is the cheapest option. It will also be the cheapest option in the developing countries. So forcing high cost electricity on Australia will make no difference to world emissions. I’d agree with your statement if we can remove the impediments to low cost nuclear. Until we are prepared to do that, nuclear will remain a high cost way to generate electricity in Australia.
Harrywr2,
Thank you for those excellent explanations about why labour costs more in Australia than in USA. Before I read your comments I’d written the response below, which I will post even though you have provided excellent explanations.
Martin Burkle, on 4 November 2011 at 2:51 AM
Well done. You have zoomed in on one of the critical issues that are making nuclear much higher cost than it should be. There are other factors too, but let’s deal with this one here and hope others may find and point out the other impediments to low cost nuclear.
The EPRI report gives a breakdown of the labour rates and the productivity factors that combine to make the overall factor of 1.71. The method is not new. EPRI and others have been doing this for a long time. EPRI did similar for converting US costs to Australian costs for coal and nuclear for their 2006 report to the Uranium Mining, Processing and Nuclear Energy (UMPNE) report for the Howard Government. In that they explained how they calibrated the figures. http://pandora.nla.gov.au/pan/66043/20061201-0000/www.dpmc.gov.au/umpner/docs/commissioned/EPRI_report.pdf
The reason is not quite as simple as that. It has more to do with our industrial relations environment. (Deleted un-supported personal/political opinion)
In short, Australia’s labour component of the NPP would cost some 1.71 times more than in the USA, and the USA’s labour component would cost more than in Korea or UAE. If the local labour component is 50% of the total capital required, and if local labour cost is say three times Korea’s, then the capital component of an NPP in Australia would be double the cost of the same plant in Korea.
Peter Lang,
http://www.bbc.co.uk/news/world-asia-15552687
Bangladesh has agreed to build two new nuclear power plants with Russian help as the country looks to close a yawning power deficit.
The developing world has impediments other then cost to adopting nuclear. The EPRI price comparisons if one put in Bangladesh labor rates and coal extraction costs would look completely different.
Harrywr2, or any one else, can you provide a link to a breakdown of the capital cost of a new NPP (such as an AP1000 or CANDU 6) into its component parts such as (or how ever else it is presented that allows us to differentiate the loacl costs from the procured costs):
components procured internationally
local industry (called Australian Industry Involvement here)
local labour
Owners costs
AFUDC
@Peter
Thanks for more detail on labor costs. I have been looking at this site http://www.bls.gov/fls/ which compares manufacturing labor productivity (and other stuff). This report also shows huge differences between countries. There is much difference between countries in the EU. There is much difference between countries in Asia.
So your question about AP1000 labor costs broken down by what must me done locally and what labor can be done in another country is a very important question. Of course the reactor vessel, the steam generators, the pressurizer, the turbine, the containment vessel, the valves, and the large pumps will be made off shore. (most of these are not made in the United States either) But there are 200 piping, and wall modules that could be made off shore also. If you made everything overseas and assembled locally, how much local labor is involved?
As long as we are thinking about labor, has anyone thought about operations labor? The AP1000 advertising talked about only 400 people needing to run a plant, but I think another 100 got added for security after 9/11. So if 500 people are needed to run a plant in the US, do you think a lot more would be needed in Australia? (Deleted unsubstantiated industrial relations figures)
Is it reasonable to think maintenance and operations would be the same in Australia as in the US? Maybe quite a bit higher (like 1.7 times?) This also would make nuclear less attractive.
MODERATOR
Please support your contentions with references.
Gene Preston — Actually, planting trees starts removing significant quantities of CO2 from the atmosphere right away. For the scale required for tree planting as the sole solution, begin with
Irrigated afforestation of the Sahara and Australian Outback to end global warming
http://www.springerlink.com/content/55436u2122u77525/
Small modular reactors (SMRs): First oof, TVA is interested in the B&W mPower but the type does not yet have NRC approval. The first SMR to obtain type approval from the NRC will be the Nuscale 45 MWe unit, in 2018-2019. It is to be built in a factory and shipped to the site, just as will the other components.
The local construction includes the civil component, foundations, concrete walls, enclosures for the so-called nuclear island and the turbine island. The remainder of the construction invovles some extremely careful pipe-fitting; more so than for a coal or natgas fired unit at least in the USA with the NRC inspectors popping in all the time.
Using figures in the NREL sLCOE calculator which work well for the USA, to achieve an LCOE of US$0.055/kWh reires that the total capialt costs, everything included (such as finace changes during construction), to be but US$2070/kW. I find that so low as to be not credible, even for a SMR. Doubling to US$4140/kW gives an LCOE of US$0.083 over the 30 year life of the loan; this is a credible figure for the USA provided the site has neither additional water nor transmission costs.
I’ll crudely estimate that local labour is 33% for the US$4140/kW. So using Pater Lang’s estimate of multipllying by 1.7 for the situation in Oz, I obtain US$6906/kW for an LCOE of US$0.122/kWh (which is approximately the expected USA average busbar costs for electricity in 2020 CE). I opine this is affordable.
Martin Burkle — In the USA NPP operators are well trained and amply compensated; for those reasons I doubt more operators would be required in Oz. Incidently, it takes hiring 7 people to have one always on duty 24/7/52.
David Benson and Martin Burkle:
Re: “To think that the labor component would be 1.71 times more than in the US is really hard for me to believe.”
Agreed. Thus far, I have not seen clarification of this figure in sufficient detail to eliminate the possibility that EPRI selected a high-cost nation (USA) for its base prices and then overloaded the labour rates. I’m always a little suspicious of rats in the ranks… did, perhaps, the Australian Government, when establishing the ground rules, put a thumb on the scale, perhaps two thumbs, in order to ensure that the nuclear power prices were pessimistic? Maybe, EPRI did not set this factor alone, it may well have done so in concert with a client whose published long term anti-nuclear stance led it to this outcome.
Alternatively, how much of that 1.71 is a loading for FOAK construction?
Of course, I do not know the answer to these questions. That doesn’t stop me from wanting to know, because the cost of NPP’s appears to be extortionate when compared to international examples.
This aside, well done, Peter Lang. This study is the result of considerable effort and talent.
JB,
Thank you. With your experience in project management of NSW coal and gas power stations you be the ideal person to investigate the basis of estimates and write an article to show which components are the main drivers making the projected cost of nuclear iin Australia so much higher than in Korea and UAE .
I’d suggest the first step might be to check and summarise for readers, what is stated in the EPRI reports (2010 and 2006) and also the ACIL-Tasman (2009) report. There is also an update for AEMO by WorleyParsons of the EPRI data; it investigates the sensitivity to certain parameters as you imply should be done; for example, see sensitivity to “Productivity Rate Variations”, Section 3.3.2. Unfortunately, the Worley Parsons report has excluded nuclear in its analyses, no doubt as a result of a direction from the client Also, AEMO has on its web site the spreadsheets with the inputs needed for estimating LCOE that they provided to their consultants for modelling the electricity generation cost. Here are some references (but not all):
http://www.ret.gov.au/energy/Documents/AEGTC%202010.pd
http://pandora.nla.gov.au/pan/66043/20061201-0000/www.dpmc.gov.au/umpner/docs/commissioned/EPRI_report.pdf
http://www.aemo.com.au/planning/419-0035.pdf
http://adl.brs.gov.au/data/warehouse/pe_abarebrs99014434/energy_proj.pdf (Figures f and g are taken directly from the EPRI report figures 10-13 and 10-14)
http://www.aemo.com.au/planning/0419-0017.pdf
Martin Burkle, @ 4 November 2011 at 11:34 AM,
Thank you for that link and comment. It is very helpful. If we can all explore and contribute like this we may, as a group, be able to isolate what are the main contributors causing the high cost of nuclear in the Australia.
@ 4 November 2011 at 11:46 AM,
I have a little. However, O&M is responsible for only 15% of the LCOE of nuclear (see Table A2-2), so I haven’t focused on this. The priority, I believe, is to focus on the capital cost which is responsible for 79% of LCOE.
Peter Lang, thank you for the response.
I should have noted I was considering coal outside the available options in my statement that baseload nuclear, with only CCGT would be cheaper than options that included intermittent s which, in my opinion, can only displace baseload. I’ll try to get to reading the EPRI report.
This comment is related to the breakdown of costs for CANDU’s, and I’ll have to admit to offering hyperlinks that I have not read – they were sent to me in reply to my inquiries. They may be helpful to you.
Here’s some quick background on Atomic Energy of Canada Ltd. (recently sold for next to nothing and now part of SNC-Lavalin). Most of the builds in the past 25 years were foreign and came in on time and on budget. Domestically the last reactor entered operation in 1994, which was the fourth Darlington unit. That project was stopped and started multiple times during the high interest 1980′s. Predictably the cost overruns were huge.
So my quick glance at the one document is what can go wrong domestically in politicized environments: http://www.magma.ca/~jalrober/CANcostf.htm
The second document is the, on time and budget, Qinshan post-project analysis:
http://canteach.candu.org/library/20031701.pdf
You might find some useful information for containing costs in there – although at a glance I can’t see a neat breakdown of the cost components.
Scott, thanks for the link to the IAEA lessons learned from two Candu reactors built in China. http://canteach.candu.org/library/20031701.pdf
I especially liked the chart showing man hours by month resulting in 34.000,000 man hours for two reactors. Also, the break down of hours by type of activity. At peak there were 7,000 workers on site!
The amount of concrete, 500,000 m3, is very large as compared to two AP1000s at 200,000 m3.
These projects are really large. Aren’t they?
Martin Burkle @ 4 November 2011 at 11:46 AM
Any place with civilized / restrictive labour laws is going to need five shifts, which is what my employer runs for a 24/7 chemical plant.
40hr/week X 46 wk/yr X 5 = 9,200 hrs year, vs 8,760 hrs needed
That’s with 6 weeks holiday each. The extra 88 hrs each covers sickness, training and a bit to spare for busy times, preparing plants for maintenance etc. Four shifts plus a lot of overtime works out more expensive.
Peter Lang,
All I could find was this report which includes the assumed work days for various NPP’s on page 57(according to the pdf reader)
http://www.ne.doe.gov/np2010/reports/mpr2627DoeConstructionScheduleEvaluationRev2Final.pdf
The AP1000 construction schedule is optimized for a 5 day a week 10 hour a day work schedule.
Under US work rules the AP1000 would yield 47 1/2 of paid work per week.(1/2 lunch break is unpaid and generally staggered between 11 am and 1 PM)
By US work rules it would be 40 hours base time + 7.5 hours at an overtime rate of 1.5 base pay. = 51.25 hours of pay for 47.5 hours of paid work.
An ABWR is optimized for a 5 days a week 8 hour days plus every other Saturday. In the US a standard work day is 8.5 hours minus 1/2 hour for lunch.
The ESBWR is optimized for construction with 3 crews working 4 ten hour shifts with 2 days off.
Martin Burkle, @ 3 November 2011 at 9:59 AM:
I said in my response @ 3 November 2011 at 1:18 PM the answer to your questions is “Yes, you are comparing apples with apples”. I’ve changed my mind on that. The $20.4 billion is the contract payment to the Korean consortium. Therefore, it probably does not include owner’s cost and may not include AFUDC. Therefore the Total Capital Required is probably higher than $20.4 billion.
By the way, I understand (perhaps misunderstand) the APR1400 being built in UAE is 1,350 MW (sent out) each unit, or 5,400 MW for the four units, not 5,600 MW. So the Total Plant Cost would be $3,778/kW (2010 US $).
Scott Luft @ 4 November 2011 at 12:56 AM
Your comment demonstrates why the analysis presented in the lead article is valid and useful.
This would be true if nuclear was cheaper than coal. It is not true if nuclear is more expensive than coal.
In Australia’s case our electricity is generated by:
Coal = 76%
Gas (predominantly OCGT) = 15%
Oil = 1%
Renewables = 8% (of which 5% is hydro)
If we want to replace the coal component first, and do it as you suggest, 76% of our electricity generation needs to be replaced by nuclear and CCGT.
The National Energy Market Demand (eastern states) is about:
Minimum = 17 GW
Maximum = 33 GW
So, applying your suggestion, we’d need to replace 17 GW of coal with nuclear and much of 16 GW (33 -17) with CCGT.
While nuclear is more expensive than coal, we will not implement nuclear. We will start by building the CCGT.
The analysis in the lead article helps to expose the problem we face: nuclear is too expensive to be seriously considered as an option for Australia. That is the reality.
Unless, of course, we expose a major flaw in the EPRI figures (and all the other consultants’ reports which reach effectively the same conclusion that nuclear is too expensive for Australia).
Scott Luft @ 4 November 2011 at 10:32 PM
Thank you for that information. I should let you know that I have kept somewhat up to date on AECL and CANDU but do not have all the recent figures. I worked on the Wolsung Unit 1 (CANDU) during construction and the site investigations for the Preliminary Safety Analysis Report (PSAR) for Units 2, 3 and 4 back in 1980. I also worked for AECL at Whiteshell on the Canadian Nuclear Fuel Waste Management Program and was on site from the start of construction of the Underground Research Laboratory. I also worked with and visited most of the other waste management programs throughout the world including Yucca Mountain, Sweden, Switzerland, Germany and UK between 1983 and 1989. So a bit out of date and out of touch now, but just thought I’d give that background.
Realistically, we do not have any up to date costings for CANDU 6 other than China. So we need to scale those figures to Australia, probably via USA, along the lines of what EPRI has done.
I’d say to others following this thread, and especially those criticising the EPRI report, I believe EPRI’s conversion methods and factors are as good as we have. Just saying that we don’t like the result is not a convincing argument. If we want to tell the government departments who are using the data in their modelling (and AEMO and Energy Supply Association of Australia and many modelling and consulting organisations) that the EPRI work is wrong, we need to do better than say in effect “we don’t like the numbers EPRI has come up with”.
Again by following World Nuclear News one learns that there is a local contractor other than the South Koreans on the UAE project. The local contractor appears to be doing site preparation work, at least right now. Therefore the contracted price to the Korean consortium is not the full cost of the UAE project.
In concluding that CCGT is the preferred form of baseload now I think we should factor in steep price rises for gas. I note that a gigajoule thermal is 0.28 Mwh thermal. If the latest CCGT plant is 50% efficient then that becomes 0.14 Mwh electrical. Therefore if new contract gas is $7 per GJ in Victoria (expected for the Mortlake plant) then the fuel cost per Mwhe will be some 7X that, say $50.
What if the fuel cost went from $50 to $100 in a decade? Here are some reasons I think it could happen
1) regional supply imbalance
The south eastern States SA, Vic and Tas will be begging for gas by about 2025. It is conceivable that the Federal govt may have to force gas rich parts of Australia to share gas with the SE. That probably means paying export price, noting the Japanese recently paid $10 a GJ for LNG
2) transport demand
Natural gas vehicles are popular in Iran, Pakistan and Argentina. Currently heavy vehicle operators here can pay as little as $1 a litre if they are eligible for a rebate. I think when truckers have to pay $2/L there will be a wholesale shift to gas fuel, LNG for big rigs and CNG for urban vehicles. In thermal terms that means their price point is over $50 per GJ and they will out-compete stationary users like power stations. Again the Feds may have to intervene.
3) fracking foibles
It will only take one upset farmer to win a court case for damage to his bore water supply to force a rethink on CSG. Then claims of 250 tcf or ~5 bn tonnes of CSG will have to be reviewed.
Therefore claims new gas fired power stations will be built in places like Roxby Downs SA and Yallourn Vic are suspect. It would require the Feds intervening to ensure a long term cheap supply.
harrywr2, @ 5 November 2011 at 3:02 AM
Very interesting information. Thank you for that. I am not sure how we can use it, but good to have it for future reference.
I am not intending to try to check the EPRI report. I am going to accept their figures as OK and use them. I feel if they were wrong someone would have picked it up by now and the government would not be using their figures as an inout for their modelling. The fact that AEMO contracted WorleyParsons to run sensitivity analyses on the EPRI key inputs, such as labour productivity factor, shows that others have asked similar questions and AEMO responded by contracting Worley Parsons to do an independent check. I believe the issue has been dealt with.
I feel we need to start with something. So unless someone else can show clearly there is a serious flaw in the EPRI figures, then I urge we accept the EPRI figures and get on with working out what we need to do to remove the impediments to low cost nuclear in Australia.
I hope the Moderator will allow me to repost these two comments from the “Alternative to Carbon Pricing” thread. The thread is frustratingly slow to respond and I understand why readers will not read comments on that thread because of the slow response. These comments are directly relevant to this discussion.
http://bravenewclimate.com/2010/01/31/alternative-to-cprs/#comment-109730
28 December 2010 at 10:00 AM
http://bravenewclimate.com/2010/01/31/alternative-to-cprs/#comment-109732
28 December 2010 at 11:29 AM
David, I can hardly get trees to grow in my yard. How in heaven’s name can we possibly get trees to grow in the Sahara desert?
@Peter,
While nuclear is more expensive than coal
The EPRI estimates for IGCC coal are based on a ‘theoretical plant’.
The US ‘demonstration plant’ for IGCC technology at Edwardsport, Indiana is 50% over budget. Now estimated to be US$2.88 billion for a 618MW plant.
http://www.reuters.com/article/2011/10/20/utilities-duke-edwardsport-idUSN1E79J20S20111020
The second proposed coal IGCC 600MW IGCC demonstrator is budgeted at US$2.4 billion with a US$2.88 billion cap set by the regulator.It’s got some legal problems and may not get built.
http://msbusiness.com/tag/kemper-county-coal-plant/
Gene Preston — Making the trees grow requires drip irrigation, Israeli style. The full article (which is free for you to download) estimates the desal and pumping costs (although should be somewhat higher).
Maybe the DesertTec porject, which is going forth, could actually be put to some good use this way…
Harrywr2,
The lead article for this thread does not include IGCC for the very reason you mention. Nor does it include geothermal or most of the other 43 technologies EPRI provided figures for. I selected the six most viable and/or most advocated technologies. These make the point clearly: nuclear is not cost competitive in Australia nor is it the least cost way to reduce emissions at this stage. Therefore, nuclear will not be given serious consideration by governments while this situation remains.
Harrywr2,
I should have said ‘thank you” for providing those up to date figures on the demonstration IGCC plants. I am sceptical that IGCC, CCS, geothermal, solar thermal or PV, wind, biomass, or any ot the other renewable energy technologies will ever be realistic options for supplying a significant proportion of our electricity. I doubt any of them will be economically viable. I do believe nuclear will be, eventually. The question is when. When will we do what we have to do to unwind the mass of impediments we’ve imposed on it over the past 50 years as a response to anti-nuclear activism.
Harrywr2,
just to clarify, what I mean by the sentence of mine you quoted:
is that LCOE of nuclear is 4.5 times the LCOE of existing coal generation and twice the LCOE of new black coal generation.
“• IAEA – what are the minimum requirements and how have they been implemented at least cost in other countries with small economies?”
How does IAEA work? By this I mean who joins? Does the government of Australia join? If the government, is this thru a treaty or does some federal department pay dues?
or would the a group interested in nuclear join?
On the IAEAs web site I found a meeting of many middle east countries that do not have nuclear power plants conducted by the IAEA. So could some professor or doctoral student from Australia attend IAEA meetings and accumulate best practices?
Why build bridges to IAEA when nuclear is clearly off the table for many years? I suspect that when the politics changes the change will be very rapid. So being prepared is one reason but more importantly would be to develop experts that can inform another EPRI committee about the best nuclear choice for Australia. It seems that the experts on this blog know a lot but not enough to actually lay out a plan once the politics is in pace.
How do you set up a regulation body? Which countries methods would best to emulate?
The Chinese Candu took 17,000,000 hours to assemble. I have read that the AP1000 takes 5,000,000 hours to assemble. I bet the IAEA is the best place to learn which number would be closer to the Australian number.
Does the UAE contract include ground work? owner cost? I bet the IAEA is the best place to get such information.
So how or who needs to become active in IAEA?
Martin Burkle — I previously answered some of your questions regarding UAE; all I did was repost what I learned from following World Nuclear News.
I’ve also earlier (and probably on another thread) offered the opinion that Australia might well wish to follow the British regulatory model for, not the least, its reponsivieness and the demonstrated competence of regulators and NPP operators.
Martin Burkle,
Thank you for your comment.
Australia is active on the IAEA. In fact, the IEA’s investivgation of Iraq’s ‘weapons of mass destruction’ (nuclear weapons) was led by an Australian (until he became Governor of Tasmania!).
Our research and medical isotope nuclear facility at Luca Heights and ARPANSA are active in the IAEA.
The IAEA is an excelelnt source of information.
What I am hopong is that others who know a lot about the subject and have speciif relevant skills will do some research and post the results on line. What I believe we want to identify is how much the LCOE could be reduced. We need to break it down into component parts and focus, initially, on the components where there is most opportunity to reduce the LCOE. Clearly, since Capital is 79% of LCOE, that is the place to focus attention initially. Capital can be broken down into components. On another axis are the influencing factors, such as labour rates and productivity factors, investor risk premium, etc.
I hope we can encourage the many experts who contribute to BNC (and the many more who are reading and watching) to get involved in this exercise.
David B. Benson – Thank you for that link to the “Sahara forest” paper, that was very interesting.
DBB,
Yes, the UK regulator regime might be preferable to the US. But others may be better still. What is needed is a quantification on the effect on the LCOE, not just fot one plant but for 50 years or more of nuclear build and operation. Would you like to take on a research project to quantify how much savings on LCOE, if any, Australia could achieve by tieing into a nuclear regulatory program run by USA, Canada, UK, EU, Finland, Sweden, Russia, Japan, China or India.
Peter,
You have written a perfect description of a doctoral thesis!
“Would you like to take on a research project to quantify how much savings on LCOE, if any, Australia could achieve by tieing into a nuclear regulatory program run by USA, Canada, UK, EU, Finland, Sweden, Russia, Japan, China or India.”
Where would you find such a student?
Peter Lang — You left off France!
🙂
Japan’s scheme will surely be unpopular in Australia and China has decided than a mere 300 regulators is too few [given the number of simultaneous builds, I agree]. The UK scheme has the NPP owner paying for 98% of costs of regulation; surely popular with tax payers if not rate payers.
Fleet average LCOE goes down as realized capacity factor goes up; the cost of regulatory services is negligible in comparison.
DBB,
The cost of the regulatory services may be negligible. But the cost of the excessive regulatory intrusion in nuclear energy is enormous. According to Cohen, regulatory ratcheting has raised the cost of nuclear generation by a factor of four. I’d assert that is for no real benefit. In fact it is a massive disbenefit. It is costing the world tens of thousands of lives and many more illnesses and disabilites per year. I’ve seen figures (I don’t remember where) that polution from coal fired power stations in USA causes 24,000 early fatalities per year (anyone have the source for that figure? Is it considered authoritative?).
I suspect if we have to fall under the US NRC, the cost of nuclear will be much higher for ever than if we could fall under am much leaner regulatory environment. For example, I’ve seen how the US EPA continually changes the rules for emissions regulations [1]. They’ve been changing the regulations every few years for 30 odd years. The cost to industry must be enormous. I suspect it would be even worse with the NRC, wspecially during the FOAK period for new reactor types.
[1] http://www.epa.gov/airmarkets/business/ecmps/docs/ECMPSEMRI2009Q2.pdf
Martin Burkle, @ 6 November 2011 at 12:45 AM,
I reckon you’d be ideal! Are you offering? 🙂
Actually, being serious, this is what I think on the issue of “nuclear is too expensive to be a realistic option for Australia”:
There are many people contributing to BNC who are highly knowledge about the relevant subject material, have excellent research skills, have background to enable them to know where to look and to zoom in quickly on the relevant material.
So I am hoping these people might volunteer to take on bits of the task.
The first hurdle we need to get over is for the contributors who are finding the message confronting (I’m not referring to you, by the way, you are one of the few left contributing on this thread) – that nuclear is too expensive to be viable in Australia – to recognise this is a fact.
Once we get over this denialism (a BNC term), we can move forward.
If in the meantime, if some people want to drill down into the EPRI figures and find a gross error – or find an error in my analysis – then that is all valuable too. We do not want to set off on a path based on a wrong starting position.
Peter Lang — The NRC has agreed to give up so-called regulatory racheting by issueing type licenses. For example, the type license for the Nuscale 45 MWe SMR will require 7 years if all goes well. The UK regulatory is much nimbler, so much so the Hyperion appears likely to build its SMR in England as the type approval won’t require anything like the ~21 years the NRC would likely spend on that [my guess], given that its not an LWR but instead a (just barely) Gen 4 lead cooled unit.
All LWRs encourporate much the same safety features which were add-on during the period of ratcheting; only the Areva EPR has substantial additional features [and doesn’t seem to have a type license in the USA yet].
Your remarks about the US EPA demonstrate your failure to understand the applicable laws under which the EPA makes and enforces rules; these decrease LLE and so are generally thought to be a good thing [I certainly do]. However, as recent events in Japan have amply demonstrated, the LLE from NPP mishaps is so low as to be almost unmeasurable. I recommend reading Professor Cohen’s “Understanding Risk”
http://www.phyast.pitt.edu/~blc/book/chapter8.html
(Deleted inflammatory comment.)
DBB,
(The comment to which you refer has been deleted.)
You’ve completely missed the point, I think. Nuclear is too expensive. It is not competitive. Largely that is because it has been regulated to be overly expensive as a result of 50 years of anti nuke activism. To make Gen IV and new SMRs least cost we need to completely revamp the nuclear regulatory system.
(Snide remark deleted.)
But, obvioulsy I’ve jumped too far ahead on this thread.
To all, let’s get back to the lead article. Are there any errors? We need specifics if I am to change anything. Simply saying “we don’t like the result” or “we don’t agree with the labour productivity figures” is little help. The figures proposed instead need to be justified. Otherwise, it is just a case of “I don’t like what you are saying”.
Peter Lang — The world population has agreed to go with (essentially) NRC’s PRA safety criteria, no matter how much anyone thinks making NPPs as safe as eating peanut butter is overdoing it. Therefore NPPs are expen$ive but in most of the world not appreciably more and often less than other forms of low carbon electricity generaation.
In an attempt to lower the costs of NPPs, Nuscale devised their 45 MWe SMR, whose simplicity and even elegance is prehaps best appreciated by engineers. Following on much the same thought B&W’s 300(?) MWe mPower SMR might be a larger version of much the same design ideas which keep or improve on the ‘eating peanut butter’ safety while lowering costs rather dramatically [by NPP standards, that is]. I have offered an approximate LCOE for the Nuscale unit if built in the USA and even made a stab at the cost in Australia using your labour multiplier. I suspect that the B&W mPower, still to receive NRC type approval, will be about the same price; whatever that price is, it will be less than for the Westinghouse AP1000 and the Areva EPR.
There is essentially nothing which can be done to change the required safety or anything else which might be a cost driver. I personally suspect that Australian EPRI(?) study is biased or otherwise contains a mistake; the e3 study commissioned by the State of California also priced NPPs way too high, that in a state which had already forbidden any new NPPs. I suggest that influenced the e3 study and I repectfully suggest the same mght be true of the Australia EPRI(?) study. However, I have no competence enabling me to critically read either cost study; I just note that both are completely out of line with what is occurring elsewhere in the world. Maybe Australia, just like California, is extra special.
DBB,
I guess, since you and many others do not waht to entertain the possibility that NRC regulation has cause nuclear to be massively over priced we should stick with coal until another generation wakes up to what we’ve done.
There is not point me trying to explain what I am trying to say to you. I’ve tried too many times, and it is going nowhere. So please understand why I do not bother responding to your comments. I find them mostly unhelpful.
[…] Posts CO2 abatement cost with electricity generation options in AustraliaFukushima Nuclear Accident – a simple and accurate explanationOpen Thread 19Geographical wind […]
Thanks to Peter and to all contributers for an interesting thread.
Peter, I noted with interest in your paper the sentence
” Nor do the emissions intensities include the higher emissions intensities produced when load-following; e.g. when cycling power up and down to back-up for intermittent renewable energy generators”
I have seen figures suggesting that the thermal efficiency of the best OCGT’s is around 40%, and other figures suggesting that the thermal efficiency of the best CCGT’s is around 60%. Even if the latter figure is overstated and should be around 50% as mentioned in passing in some places in the above thread, the use of OCGT’s certainly represents a sub-optimal use of the finite CSG resource.
Now I observe that GT’s backing up wind and solar cannot use closed cycle, as the steam turbine section cannot vary its output sufficiently quickly to follow the potential generation variations, and the ST also requires the GT to be working at near full output to operate anyway. So: we have OCGT backing up “unreliables” [http://bravenewclimate.com/2011/10/29/gws-sg-es/]. Running as backup, these OCGT’s will not be achieving their full thermal efficiency. So we have WT’s etc plus OCGT’s at, what, 30%?
Now one alternative to that is to scrap the (WT’s etc) bit and install CCGT’s at 50% instead. I am left wondering whether the CO2e/kWh figure of the latter will actually work out near equivalent to the former. The latter will certainly be a more productive use of the CSG, and would require far less investment in resources and infrastructure.
Has anyone figures to verify or disprove this conjecture?
Phil Spencer,
Thank you for your comment and question. Most regulars on BNC would agree with the point you make. There are many articles on this on BNC. I’ll point you to three for a start, and suggest that many of the comments will be of interest too:
CO2 avoidance cost with wind energy in Australia and carbon price implications
http://bravenewclimate.com/2011/05/21/co2-avoidance-cost-wind/
Replacing Hazelwood coal-fired power station – Critique of Environment Victoria report
http://bravenewclimate.com/2010/05/29/replacing-hazelwood-coal/
‘Zero Carbon Australia – Stationary Energy Plan’ – Critique
http://bravenewclimate.com/2010/08/12/zca2020-critique/
You may also want to download the spreadsheet linked at the top of this thread. Unhide columns L, M and N and change the inputs to suit your assumptions. Use the NREL calculator to calculate LCOE if you need to change capacity factors or any other input that affects LCOE.
Peter Lang,
I could purchase 1.5 kW for $7500 US dollars if I were given the opportunity. That would supply about 12,000 kWh for a year for the next 60 years. How can that be too expensive? Its the cheapest energy source out there, Nuclear’s problems are only institutional.
Gene Preston, on 7 November 2011 at 12:06 AM said:
I could purchase 1.5 kW for $7500 US dollars if I were given the opportunity. That would supply about 12,000 kWh for a year for the next 60 years. How can that be too expensive?
Mine mouth coal prices in Australia are similar to mine mouth coal prices in Wyoming. In the neighborhood of $1/GJ. In addition Australian coal has a very low sulfur content so SO2 scrubbers aren’t required(according to the EPRI report Peter referenced)
In the US the overwhelming majority of the population lives a very long way from Wyoming. Once one calculates in the transmission costs or the rail transport costs from Wyoming coal doesn’t look all that competitive.
Gene Preston,
You claim is un-substantiated. Can you explain how you derived the figures and provide all the sources for your assumptions and inputs. Need to use accepted accounting methods and LCOE analysis methods (please use the NREL calculator so we can all follow it.
Do you have any problem with the analysis of the EPRI data presented in the lead article?
If you dispute anything in the EPRI report can you explain the error and provide a replacement value.
For all contributors, I’d suggest, at this stage it would be unhelpful to have any more comments which amount to no more than “I don’t like the figures in the EPRI report”. If there are errors let’s substantiate them and quantify them.
The $7500 per 1.5 kW is $5000 per kW. The price of the South Texas Nuclear project units 3 and 4 at $5000 per kW for 2700 MW is a total price of $13.5 billion dollars, which is higher than the estimated project cost. Under my energy annuity concept severa million customers buy into the project by making cash flow investments over a period of 5 years. The customers investing do not charge interest but expect to get in return low cost energy for a very long time into the future. So with this model there is no interest during construction. There is little uncertainty by the builder that the money will be available because the individual customers want to buy into the project and have signed an agreement to make the payments over 5 years to pay for their share which they will own when the plant comes on line. Then the O&M cost is expected to be about 1.6 cents per kWh after the plant is running, which is the current STP O&M cost. So the investory pay the up front capital cost which is low, and then pay a very low energy cost when the plant is running. The contract with the utility allows the energy received from the plant to be taken into account and lowers the kWh supplied by the utility for production. The utility supplying the customer charges for T&D costs and charges for any energy above the energy taken from the nuclear plant, so the utility does make money, but not on resale of the nuclear energy, which is wholesale to the customer investing. The only problem with this idea is that the utilities oppose it and its not allowed in Austin Texas where I live. When the lights go out, I will demand that indivudual customers be given an opportunity to invest in their own power sources. The lights may go out this summer because the ERCOT grid is becoming extremely short on capacity with its energy only markey. The LCOE has nothing to do with my analysis. Do you do a levlelized cost analysis when you buy a new car. Heck no.
All right, Gene, let’s avoid using the more appropriate LCOE calculation and take a look at your figures. We will, amongst other things, ignore the time value of money and the cost of R&M. We will presume, quite unreasonably, that every single unmaintained, geriatric panel remains in service for 60 years.
Let’s do a quick comparison based on 20 years panel life, which is closer to the claims of most panel manufacturers. Perhaps you could provide a quote indicating that panel cost, inverter and controller, support frames and installation are commercially available at your stated price of $7500 and that no inspections, maintenance or repairs will be needed during the 60 year guarantee period – presumably, this is included in the price and at the supplier’s risk. Good luck with that. However I will use your figure.
Now it’s time for my own unsupported assumptions:
1. 5% degradation of panel performance annually.
2. Zero maintenance cost. Yes. I know, impossible, but favourable to your case.
3. Capacity factor of 25% (again, generous).
Results:
First, the annual output is not 12,000kWh as claimed. It is 3247.5kWh. You overestimated by a factor of 3.7, right at the outset.
Panel efficiency after 60 years is only 4.8% of its original, ie 72 watts.
Lifetime kWh (60 years) = 62 MWh.
Lifetime kWh (20 years) = 40.4 MWh.
Average cost (60 years) = 12.105 cents/kWh
Average cost (20 years) = 18.6 cents/kWh
If, as per the second post, an O&M cost of 1.6 cents per kWh is included, the energy costs become:
13.7 cents/kwh over 60 years
20.2 cents per kWh over 20 years.
Compare this with 5 to 8 cents per kWh LCOE for new nuclear power in USA. Ref: http://www.oecd.org/dataoecd/59/50/45528378.pdf
So, even using Gene’s own very questionable figures and after correction for the capacity factor, the solar power proposal is nowhere near the money.
Of course, this would change if the sun shines 24/7/365 in Austin, Tx and no cloud ever obstructs the sun’s rays. That’s where the cf comes in. Even an optimised, two axis tracking system was installed to keep the panels perpendicular to the sun’s rays, the hypothetical capacity factor will still be 50% minus dirt, degradation, cells out pending maintenance or replacement, etc – say 40% in lieu of the assumed 25%.
I submit this to demonstrate the differences between a used car salesman’s view of solar costs and LCOE. This is why Peter Lang’s request for LCOE calculations is relevant. Unless costs are levellised and based on verifyable real world prices, comparisons will always lie along a continuum, somewhere between error-prone and fraudulent.
Ev
John, there is no panel. There is no inverter. I am talking about investing in a partnership in a 2700 MW nuclear plant, namely STP 3 and 4. Nothing changes at my house. The only thing that is different from a utility building the plant and a million customers investing is the ownership and where the money to build the plant comes from. Also the accounting of kWh at the customers end and at the nuclear plant end must be accounted for and matched up for each customer. I am only talking about a nuclear plant, I am not talking about a solar plant at all.
John Bennetts — Gene Preston is aattempting to explain another way to finance an NPP; his post has nothing whatsoever to do with solar PV.
The LCOE calculations remain the same; the capital costs have to be recovered somehow but an alternate to the current financing methods in the USA is to be welcomed.
Gene Preston,
Before we get into your analysis, can you please cite sources for the figures for:
Total Plant Cost
Owners Costs
AFUDC
Total Capital Required
Fixed Operation and Maintenance
Variable Operation and Maintenance
Fuel costs
Book Life
Discount Rate (before tax)
Capacity Factor
We’ve been through your idea before on another thread. I wasn’t persuaded then and there is nothing new to persuade me now. I explained my issues with your proposal on the other thread (as did others). One of thee issues is that small investors demand a shorter payback period (higher return on investment) than large institutional investors. The small investors are more risk averse. So the LCOE will be higher, not lower.
Another reason was the problem of ownership of the shares and liquidity (when someone wants to sell). Would shares be traded on the stock market? Can anyone buy them? If not how will there be liquidity? If they will be traded, how is this different to any publically traded company? If it is not different, wouldn’t it be cheaper and safer for small investors to buy shares in the electricity utility?
I don’t buy that.
I believe this is a pie-in-the-sky idea. My reaction is that it is too far out in left field to help this thread. I’d urge any further discussion of this be taken up on your original thread on this subject.
My apologies to Gene. When I read his solid block of text it appeared to swing between solar and nuclear – once my mistake had been made, I failed to realise that the contribution was about NPP’s, not solar as compared with NPP’s.
It’s amazing what a bit of inattentive reading can do, and how resistant the brain can be once the initial (quite wrong) conclusions have formed. So, apologies to Gene.
That leaves unaddressed the 8660 productive hours for solar PV in Texas, or have I misinterpreted this as well?
Frankly, even after several readings of the first two contributions, I remained confused as to what, precisely, Gene was talking about, apart from the well-known fact that ERCOT is presently light on for capacity. Is this not some kind of indication that LCOE analysis brings things together, in fair comparison, for objective analysis?
Was Gene discussing NPP or solar in his first comment? He did not say which. If NPP, who ever heard of a 1500 watt NPP?
I was still lost, till at the third try, Gene explained – we are discussing a part share in specific NPP proposals. But why say that LCOE is not relevant?
So, Gene, my apologies for being unable to understand your contributions. The rest is history.
Gene Preston’s comment does raise an interesting point about ownership. I understand the Finnish utilities have combined to own the EPR being constructed. I seem to recall there is a very innovative (typically of the Scandinavians 🙂 ownership arrangement. Perhaps one of the Finnish contributors could explain it and what are the perceived benefits of that arrangement.
Before we get into your analysis, can you please cite sources for the figures for:
I will give the perspective of how I see the financing as an investor.
Total Plant Cost NRG says 10 billion direct capital and 13 billion with IDC for 2700 MW http://www.nuclearenergyfortexans.org/nuclear_energy_news.php?id=38
Owners Costs Owners are the small customers investing, which is 10 billion.
AFUDC none, the owners pay as invoices for construction are issued
Total Capital Required 10 billion since there is no interest during construction
Fixed Operation and Maintenance These three items are currently 1.6 cents per kwh as NRG is billing Austin Energy, I got this figure from NRG.
Variable Operation and Maintenance
Fuel costs
Book Life at least 30 years
Discount Rate (before tax) none because thats not the way it is financed
Capacity Factor at least 95%, STP 1 and 2 set records for performance at 98% CF http://www.winregioniv.com/stpnoc04-10.pdf
Peter we are not financing this plant the way you are thinking so your LCOE analysis does not apply in this instance. Simply compare the up front out of pocket cash to get a power source going and the cents per kWh operating cost. Thats all we are looking at here. Now compare the out of pocket case for another source and the cents per kWh energy cost. Gas would be cheaper out of pocket but the cents per kWh O&M cost would be higher. Solar out of pocket cost is out of sight. Wind would not be bad, but your source of power would be on one minute and off the next.
LCOE is the way a utility would look at the different types of plants as EPRI has done. One problem with LCOE is that if you think a project is not going to fly, then the interest rate is high. If you think the project is reliable and no problem, then you finance it with a low interest rate. In this sense, the fear of nuclear by utilities and the government is what makes it unattractive financially. That fear jacks up the interest rate. In the case of ERCOT, the DOE said the interest rate would have to be 11%. Yikes. The project is not economic at 11% interest for financing. What went wrong? The proglem is that the ERCOT market design doesn’t allow the utility owners of the plant to charge in their rates the capital cost. How is the nuclear plant going to be paid for? The DOE knew this problem with the ERCOT market design so they jacked up the interest rate to 11%. They had no choice. Now if the market design here allowed utilities to finance the plant in a different manner, then the interest rate might have been as low as 5%. So you see, when someone posts LCOE with certain assumed interest rates, they basically don’t know what they are talking about unless they are very familiar with the particular market the nuclear plant is attempting to be constructed in. The problem here in the US is that deregulation has ruined the ability to finance large nuclear plants. If you want to see more about the evils of deregulation here in the US see this interview: http://www.hd.net/blogs/the-un-banked-dr-jeffrey-sachs/
So what I was trying to illustrate is that there might be a whole new way to finance these large projects. If utilities and the government are not able to finance them, then let the customers themselves finance the nuclear projects as a coop effort. Once individuals begin financing plants, all the LCOE stuff goes out the window. Individual customers can look at their money any way they want to. I think they would only be interested in 1) our of pocket cash, 2) what energy do they get and for how many years, and 3) what is the cents per kWh they will have to pay for the energy on top of what they have already paid. If you look at the individual’s investments, they will find their investment in nuclear for nearly the rest of their lives will have been a wise investment and not all that hard to finance. So lets get the show on the road and let individuals form coops to build their own plants for their own energy needs. Get the governments and utilites out of the way!
Gene Preston,
Thank you for your two articles. We have been over all this before on the thread you wrote on this very subject: http://wp.me/piCIJ-UK .
You do make some interesting points. In particular you’ve pointed out that the discount rate used in comparing technologies such as EPRI has done is for comparison purposes only. The discount rate that applies for different projects depends on the financial risk of each project. You said that you view 11% as a high rate. However, many mining projects have a much higher discount rate. I suspect the discount rate that would be applied to a NPP in Australia would be much higher than that.
EPRI (2006) points out the difference between an LCOE analysis and an analysis for an investment decision. They are quite different. I think you are crossing between the two. Australia is nowhere near the stage where we would start talking about a market analysis for a particular plant on a particular site to meet expected demand profile for electricity.
Gene, what market analysis has been done to test your idea?
• Who are the investors?
• How many of them are there?
• How much are they prepared to invest each?
• When will they make their contributions, and how much each
• What terms and conditions do they require to attract them to a coop as opposed to having the flexibility they have now?
• Have you considered why co-ops generally fail?
Some renewable energy idealists in Victoria want their own wind farms. After years they’ve managed to convince a small band of idealists to put in enough money to get two wind turbines. That’s a long way short of getting the money to buy an NPP.
You may not be interested in the financial analysis for your decisions. But most people are. Most people have an innate ability to be able to sense value without doing the analyses. Analyses of purchase and investment decisions show consumers require pay back periods of about 1 to 5 years.
I suspect if you did the market research you’d find only about 1% to 2% of the people you would need would commit to a co-op for their electricity along the lines you envisage.
Gene Preston — The investors still have to find an energy equity a good deal. There is a lost opoortunity cost associated with (instead) buying a share of an NPP. Supposing that is a net 2.5% for 30 years and supposing all up capital costs are only US$5100/kW [costs always seem to go up], I determine an LCOE of US$0.058/kWh for CF a long term realisitic value of 92%.
Assuming current wholesale price in Texas is US$0.010 and will increase at 4% pa, the LCOE for that portion of one’s utility bill becomes US$0.134/kWh. So at first pass buying an energy annuity appears to be quite a good investment. To find a better investment appears to require assuming one can net 16.7% for 30 years, which seems quite, quite unlikely.
Maybe I’ve done the analysis incorrectly, not being ‘up’ on this sort of thing…
As the designated Finn of this chain maybe I should comment briefly on the EPR constructed here. I do not really understand the pros and cons of the ownership structure of TVO (Teollisuuden voima) that owns OL NPPs. (http://www.tvo.fi/www/page/3067) TVO produces power to its owners at cost price. TVO is owned by utilities and industrial companies (mostly under Pohjolan voima PVO) and by buying shares you become entitled to a slice of the power produced by TVO.
Incidentally, the deal that TVO has with Areva for EPR is a fixed-price turnkey agreement. So the cost overruns are not directly relevant for TVO. When they sue for damages, the damage to them (as far as I remember) is estimated by taking the difference between the electricity TVO:s shareholders must now, because of the delay, buy from the market and the cost of electricity from OL3 NPP.
I am having trouble in understanding what discount rate one should use in computing LCOE. The answers can be pretty much whatever depending what choice you make. The bonds issued to finance OL3
(http://www.tvo.fi/www/page/3373/) seem to have an interest rate less than 6%.
Thanks very much Jani for providing the information re Finnish loans.
It seems that private finance tends to be available only over 10 or 11 percent (US experience, including as contributed above), while governments access funds at half of that.
The difference, the price of risk, spells death for privately funded NPP’s which are also FOAK in Australia.
We will not know the cost of nuclear power in Australia till we build one. Wasn’t this also true for renewables, of all types? I see value in proceeding to tender-box capital and operating costs asap, probably via a build-own-operate (BOO) contract. Reimbursing short listed tenderers part of the cost of bidding appears reasonable, given the need to get well researched prices, not just ambit claims. Perhaps these could be via progressive steps, with culls along the way depending on the content and quality of proposals/offers.
Until we see those prices, discussion about Australia’s comparative costs of construction and operation will remain primarily academic. Certainly, EPRI and WorleyParsons, etc estimates can only get us part of the way.
So, is the best first question not what the price is, but how to find out what the price is?
Jani Martikainen, on 7 November 2011 at 5:18 PM
Thank you for the explanation and the link. It is an innovative way to fund NPPs.
I’ll summarise my understanding of the arrangement (please correct me if I have misunderstood anything):
There are six shareholders in TVO. Each is an electricity distribution utility (or industrial company that wants a reliable supply of power).
Their shares range from 0.1% to 60.2% ownership of OL3.
Each shareholder takes their share of the electricity generated and distributes that share.
Each shareholder bears their share of the variable and fixed annual cost of OL3.
How is the capital cost of the plant paid for? Does each shareholder pay its share of each payment to the contractor as the payment falls due? Presumably interest owing is paid as the project progresses. Therefore, the total interest during construction is still a portion of the cost of the project that must be capitalised. It cannot be avoided which is what I understood Gene Preston was saying. Gene, have I misunderstood you?
I wonder if the total capital cost that is often quoted includes the owner’s costs. Do you know?
The contract is “fixed-price turnkey agreement”. The project has run over budget by a factor of two. Does Areva carry all that cost increase or is some billed to the TVO shareholders?
I understand the regulator is being blamed for part of the delays and cost overruns. Do the TVO shareholders have to pay that share?
I don’t quite understand this bit of your comment:
I’ll rewrite it in my words and please tell me if I have understood correctly
Incidentally, the deal that TVO has with Areva for EPR is a fixed-price turnkey agreement. So the cost overruns are not billed to TVO. The Consortium has to carry those costs, except where they are the fault of TVO (or the regulator? In which, case the Consortium sues TVO or the regulator). When TVO sues for damages, the damage to them (as far as I remember) is estimated by taking the difference between the electricity TVO:s shareholders must now, because of the delay, buy from the market and the [projected] cost of electricity from OL3 NPP.
What does the italic bit mean? I this the LCOE of the electricity based on the original price of the fixed price contract?
I am wondering if the mechanism for purchasing OL3 provides a lower cost and reduces risks. I wonder if it reduces the investor risk premium. I wonder how it might work in NSW. Could our electricity distributors form a similar sort of consortium to get a fleet of NPPs in NSW?
Any comments (from anyone)?
I’ll respond to your comment/question about discount rates in a separate comment.
Peter, you asked these points:
Gene, what market analysis has been done to test your idea? none, the idea is a new idea that has not been tested, its also not allowed under the current rules.
• Who are the investors? Individual electric customers including large load customers investing in off site generation which is not allowed.
• How many of them are there? Every customer in the state, probably a few million.
• How much are they prepared to invest each? large customers might put forth quite a lot of money. Small customers are unknown since the concept has never been presented to them.
• When will they make their contributions, and how much each. THey would make payments as work in progress payments come due, just like they were building a project of their own.
• What terms and conditions do they require to attract them to a coop as opposed to having the flexibility they have now? The customers have no flexibility now because the only choise they have is company x or company y, but those companies do not offer this investment option because the notion of ownership by customers has not caught on yet. In Austin which is not deregulated we have no options. There is a green rate, but it has no nuclear option. In fact the utility is anti nuclear because it is believed that the public is anti nuclear. However the utility and the city government will not put this issue before the public because if they did at least half the population her would be pro nuclear and the anti nuclear folks want to keep that hidden. They are in charge now, but their tenure is close to an end because they have not been good system planners and not the system is at risk of failure.
• Have you considered why co-ops generally fail? I know of no coops in Texas that have failed. I know of a few small attempts at solar and wind here in Austin that have (quietly) failed. Coops are not easily formed here. There was one new company recently formed called Sharyland on the border between Texas and Mexico. Its actually a rather ordinary utility so its not a coop. It was funded by the Hunt Brothers. That utility was carved out of American Electric Power. Sharyland has a DC tie to Mexico. I think they have something in mind sso that they operate on both sides of the border in some sort of bbusiness activity that is not clear as to what it is at this time.
David the nuclear energy cost of $0.058/kWh is a good deal but by paying for the capital cost up front the energy cost to those investors is much less, only about 2 cents per kwh.
David you said the current wholesale price in Texas is US$0.010. Wow we wish. Its more like five times that amount. But the generation companies say they cannot build any new plants unless the market price is ten times what you gave.
You noticed that the energy annuity seems like a good investment. It is when you consider that everyone seems to be losing money in every other kind of investment around here, House prices are depressed, stock market is failing, return on CDs is near 0% interest. There is nothing you can put your money in here that is safe except possibly gold. Being able to buy your electric power and energy for the next 30 years with a small outlay is a super investment. A great deal. Unfortunately the monopolies do not want the citizens to have that power.
Jani Martikainen, @ 7 November 2011 at 5:18 PM,
I was intending to copy the relevant sections from the ACIL-Tasman (2009) report http://www.aemo.com.au/planning/419-0035.pdf .
However, it would be best to read all of Section 2, and especially “2.2.2 Discount rate” and “2.4.2 WACC for new entrants”.
This bit (from section 2.2.1) is relevant:
Sections 2.1, 2.2 and 2.4 explain the discount rate. It is not just anyone’s pluck. It is interesting to note that ACIL-Tasman used 6.91% post-tax real WACC. EPRI provided both the pre-tax and post-tax WACC for both Current and Constant dollars. EPRI’s figure for post-tax real WACC was 7.1%, which is similar to the ACIL Tasman figure (given the analyses were done a year apart). However, EPRI used the real before tax method for calculating LCOE; using real before tax WACC of 8.4%.
The messages I take from this are:
1. Selection of the value for Discount rate (WACC) is not a matter of pick any value you want to use. It is tightly defined by the input parameters defined in Table 4 and the expression chosen for the calculation (Section 2.2.2).
2. WACC is specific for each economy and very different for different economies.
3. For LCOE to be comparable across technologies it must have been calculated using WACC that are consistent in all ways: same method, same year dollars, and post tax or pre tax, real (Constant) or current dollars.
4. It is meaningless to compare LCOE of projects that have been calculated using discount rates generated by different methods. Therefore, it is generally meaningless to compare the LCOE of technologies if the LCOE is presented in different reports.
5. These methods of calculating LCOE are not intended to be used “to evaluate an actual investment decision for a specific project” like OL3. They are for comparing a range of technologies in the planning and evaluation phase.
JB,
Good question. What do you suggest? Who do you suggest would pay for the work?
By the way, South Africa was going through the process a year or so ago. I wonder where they have got to.
Gene Preston,
The purpose of my question was to demonstrate that no market testing has been done. I’d expect a very small percentage of people (mostly idealists) would invest in the coop – similar to what has happened with the coop to buy a develop a farm (now just two turbines and struggling to get the people to actually pay for that). I am not persuaded.
@Peter: I cannot claim that I know all the details regarding the OL3 NPP so I am basically telling what my understanding of the issue is based on the media reports here. TVO:s line is that they have nothing to do with the delays and that they have a fixed price agreement with Areva for EPR. They wish to sit on the sidelines and wait until they are given the NPP they were promised and at a price agreed earlier. Areva naturally wishes to minimize their losses by attempting to dump as much responsibility for the delays on someone else so that they can avoid paying for damages.
“I understand the regulator is being blamed for part of the delays and cost overruns. Do the TVO shareholders have to pay that share?”Yes, this is what Areva claims, but to me it looks like nonsense. The regulatory regime here is not actively obstructionist and in fact on occasion the regulators have warned Areva in advance about possible delays unless they get their act together. The project has not been delayed by regulators not doing their jobs or doing it slowly, but rather because the EPR design wasn’t finished when Areva sold it. The work on control systems (which are safety critical of course) are apparently still not finished. The same concern, I think, has also been raised by the French as well as the UK regulators.
I suspect Areva was desparate to win the contract for OL3 and therefore sold the first EPR very cheaply. Their plan was probably to use it as a succesful demonstration with which they could sell more NPPs later. In the end it is hard to see what kind of agreement Areva and TVO eventually strike. Who knows… maybe Areva is desparate to win the contract for OL4 and therefore sell also that one cheaply. TVO in turn might be reluctant to buy EPR again unless Areva pays the damages.
(TVO:s funding does eventually originate from the shareholders. Just few weeks ago utility in Helsinki agreed to participate for their part in the planning of OL4 NPP. This implied costs of about 40 million euros for them. If the OL4 is eventually build, Helsinki utility would have to pay perhaps about 500 million euros for their share.)
This has been an illuminating discussion. In 2008, I looked at the question of how the nuclear industry Industries costs could be lowered. I have since 2008 continued to think about how nuclear costs can be lowered, and this discussion will undoubtedly lead me to revisit my original posts. I will not repeat my original 2008 discussions here, but most of my conclusions seem to have held up well.
One of my assumptions on Nuclear Green has been that the cost and scaleability of carbon replacement technologies is the most important issue in carbon mitigation. These issue is not being seriously addressed by most nuclear advocates, and not being addressed by renewables advocates. In addition to carbon mitigation, even if there were no CO2 problem, the ability of the global fossil fuel reserve to meet the energy demands of 7 billion people living in high energy societies is doubtful. The inability of fossil fuels to supply energy is certain. Thus lowering post carbon energy cost is of great importance to the future of human civilization.
An important feature of the TVO’s ownership model is that the electricity generated and sold to the shareholders at cost is not taxed under current Finnish legal practice, as long as the shareholders cover the operating costs. This makes the model pretty attractive to the shareholders: TVO’s dividents are in a sense paid in tax-free electricity.
This so-called “Mankala principle” (after a precedent case) applies to other energy generation as well. However, it’s now under review by the EU as a possible violation of competition law, after a complaint from two (surprise surprise) Green MEPs. I don’t know how, exactly, a possible repeal of the principle would affect the funding or the position of TVO or NPPs in Finland, other than it wouldn’t help.
Many here fear that while AREVA & co seems to be legally responsible for the cost overruns, the firm will use their connections to the French government and the EU to simply twist the rules somehow and leave the Finnish shareholders holding the sticky end of the stick. As the Russians would say, “bumaga eta bumaga, praktika eta praktika.”
One thing that I forgot to ask, was this concept of “book life”. It is clearly different than the life time of the plant. Does it not matter at all to LCOE claculation that NPP lasts for perhaps 60 years while wind turbine lasts perhaps 20 years? Or is the idea somehow to insist that the plant must pay for itself in 30 years so that one has two different LCOE:s for the same plant. One for the years 1….30 and the other from 31-60 which is only derived from fuel and O&M costs (so that it is almost free for NPP)?
A poster, quokka, has post a link to a PwC report that includes many financing suggestions for increasing renewables, all of which, it appears to me, would be ways to make nuclear appear cheaper
http://bravenewclimate.com/2011/11/06/depressing-climate-trends/#comment-141236
Section 3.3 of the PwC report is titled “innovative finance” and it includes credit and risk guarantees to increase the ‘bankability” of Power Purchase Agreements”;
financing through pension funds (public?), and/or sovereign wealth funds;
regulatory incentives,
Feed-in tariffs,
capacity payments,
a carbon price,
a ‘green’ investment bank.
“In the context of offshore wind for example, Renewables Obligation Certificates (ROCs) and the CPF only go so far in providing the appropriate investment opportunities in the industry. Policy must now address specific issues such as pre-construction financing risk that deter institutional investors from investing in offshore wind. Appropriate measures to reduce risk include underwriting technology
and construction risks via a consumer levy, regulating offshore assets, and measures to increase returns.”
Thank you for these very interesting comments. These are addressing the fundamental issue – how to get nuclear cheaper. Please keep these constructive comments coming. I’ll be back later. For now, I have three questions:
1. Is TVO one of many electricity companies that are competing. If not are there competitive pressures to keep electricity industry efficient and low cost, or is price controlled by a regulator?
2. Secondly, can any Australians add any comments about how such a financing arrangement could be applied in Australia; e.g. in NSW and Victoria?
3. This is interesting:
I believe energy, as a fundamental input to society and to human well being, should be as low cost as possible. The Finns seem to have found a way to do this. The CO2 tax concept is the exact opposite of what we should be doing, IMO.
Thank you Jani Martikainen, J. M. Korhonen, Charles Barton, Scott Luft, and quokka for the PwC link (I didn’t see it when quokka posted it ).
I’ll be back later to respond to some comments and questions; e.g on ‘book life.
Few seem to question why renewables get recurrent subsidies like REC and FIT but nuclear doesn’t. Perhaps it’s because renewables are low carbon and delightful but nuclear is low carbon and nasty. As Garnaut the architect of carbon tax pointed out it’s only the low carbon part that should matter.
I think we should make low CO2 the sole objective, provided that objective isn’t defrauded with worthless credits. If recurrent subsidies are dropped that still leaves capital subsidies, loan guarantees and insurance indemnities. Nuclear critics fail to to note the one big US loan default was Solyndra, a solar manufacturer. The biggest liability waiver in Australia is Chevron storing CO2 under Barrow Island WA. That’s a fossil fuel operation.
In my opinion we should drop the RET and the REC subsidy and focus on tough carbon constraints, be it tax or cap. The Federal govt can give capital and liability assistance as it sees appropriate to any new low carbon project. That project gets no additional assistance like a 20% quota for that technology. I’m not sure that all that much help will be required since the customers are out there waiting for energy. If that energy is high carbon they’ll have to pay more.
@ Peter Lang, on 7 November 2011 at 8:36:
Who and how to obtain competitive prices which indicate the real market price for a new NPP?
Off the top of my head, I can think of two processes which might relate to the Australian situation. First, the process selected must itself be subjected to careful analysis, or it will be a costly failure. Certainly, I don’t suggest that my thoughts are anything beyond half-baked.
All projects, to be successful, must have a leader who sets the vision and the goals. Who might this be? The answers to this question determine the shape of my tentative response.
1. Climate change is perceived to be real, threatening, a real future cost to society and thus worth committing expenditure now to drive zero CO2 electric power generation capacity. This could justify social response via a government backer, probably the Federal Government. So, the federal Government reviews ways in which to reduce future CO2 emissions, and achievable abatement costs.
The Australian Government has adopted an ad-hoc approach to this task, essentially oiling the squeaky wheels and lacking rigour in determining which projects will receive funding, from a basket of renewables, including:
Demonstration plants – Solar PV, Solar thermal, hot dry rocks, wind, wave and variants, including both applied research. Funds committed during the past 5 years or so have cost the public purse several thousand million dollars. The process has been noteworthy for its lack of openness and rigour, having (IMHO) all of the hallmarks of election gimmickry.
So, Proposal #1, Step #1 is for the Federal Government to drag the past into the sunlight, possibly via a status review of all expenditure to date, including State expenditure and State income foregone and, especially, tallying up the costs which have been fed through to consumers via retail tariffs. These include FiT’s, but also costs attributable to mandatory and voluntary renewable energy targets, costs incurred by retailers managing these programs – EnergyAustralia alone, submitted a request to the Regulator seeking to pass $75M over 4 years to all retail customers, these being the internal costs of administering the rooftop solar scheme in their part of NSW. This suggests that, nationally the hidden costs from this alone would be $100M or more.
Proposal #1, Step #2 would rely on the analysis of the data assembled above and an estimate of NPP costs and benefits – obviously, not market tested. I strongly suspect that the analysis of CO2 reductions over time versus cost will justify diversion of some of the existing social expenditure to fund a test of the NPP market, with expectation that the champion of the project would be a Federal minister, supported by developing public demand. Yes, I’m an optimist.
Proposal #2 relies on AEMO and the annual statement of generation opportunities. It is lamentable that nuclear options are specifically excluded… this is where the environmentalist George Monbiots and economic rationalists of the world have common ground.
Step 2.1: Unfortunately, is political – nuclear options must be considered on the basis of a fair comparison, warts and all. Until this is done, progress is stalled.
2.2: AEMO to oversee the process, with obvious need for involvement from ANSTO and a raft of other regulatory bureaucracies. In a perfect world, they may not be so complex, but the real world is where we and they exist, so we must deal with them.
2.3: Who pays? AEMO would proceed via an EOI. RFP documents issued to qualified respondents to the EOI. The goals would be identified via the Generation Opportunities study. Respondents to fund their own initial response – they are well capable of handling this expenditure. After culling to (say) one or two competing proposers, for a limited number of sites, the cost to bidders start to rise significantly.
I suggest that site investigations and an agreed portion of the site-specific design development and detailing could reasonably be reimbursed via AEMO in a commercial arrangement akin to an alliance agreement. This form of contract is now common in Australia, both within the power industry and throughout construction generally. Contract lawyers are comfortable with the notion of stepping away from strict contractual obligations and working cooperatively within alliances, which in my experience work particularly well on technologically advanced projects.
The output from the alliance’s work would be one or more detailed, costed proposals. Progressive review would probably further cull the proposals, ideally, down to one technology on one site.
So, Proposal 2 is driven essentially not by CO2 issues within the existing budgetary scenarios, but to extend beyond the desk studies of LCOE to produce a costed, SMART proposal by which to meet society’s future energy needs. SMART meaning Specific, Measurable, Achievable, Realistic and Time-based.
Sorry if this has become another long Bennetts post, but my intention has been to demonstrate that there are two current processes via which real bids for Australia’s first NPP could be obtained. The hold point which is common to both is the need to convert the Federal Minister into the project’s Champion, because without this, the legislative barriers will remain. My personal preference is for Option 2, on the grounds that a much wider cross-section of the community is likely to support economic rationalism or environmental rationalism (Monbiot et. al.) than the first option, which involves taking money away from virtually every renewables program in Australia, which will bring forth the renewables suppliers and their apologists, who are skilled at using PR to stifle the future of nuclear power.
@ Gene:
Re energy co-ops, one outfit in Australia is travelling this path. Google Hepburn Wind. They started with small shareholders in a specific part of Victoria, Australia. Over time, they finalised plans, have obtained approvals and, only this week, have commissioned their first 4 wind turbines – perhaps 8MW total nameplate.
Interestingly, they are now talking of spreading to many sites, still with small shareholders.
Perhaps there is something of their experience which will interest you.
A nuclear co-op is conceptually a much bigger entity, but perhaps this is not necessarily so. Packaged 45MW to 60MW units have been mentioned here. They may be an entry point, owned by and constructed for a single community.
Gene Preston — I can believe an on-peak price of US$0.50/kWh in ERCOT, although that over ten times the current on-peak price around here:
http://www.ferc.gov/market-oversight/mkt-electric/northwest.asp
and check the Mid-Columbia Hub average prices. I doubt that the average wholesale price is as large, but I certainly wish to be better informed.
Jani Martikainen — SLowly piecing together the story of the EPR, I gather it was first a cooperative venture between Areva and Siemens. A joint company, Framatom, was formed. As it became apparent that Siemens couldn’t deliver the control systems in a timely manner, Framatom became just part of Areva alone and Areva has sued Siemens for several hundred million euros. So if I have this even approximately right, Framatom, i.e., now just Areva, took the contract in Finland far earlier than they should have.
@ Jani Martikainen, on 7 November 2011 at 11:34 PM:
Jani, one thing to remember is that the discount rate has much greater impact at the start of a project than 20 years after completion.
Consider purchasing a house – the capital cost is substantial. After 20 years, even though the repayments may be the same and the principal not fully paid, the payments as a proportion of the family income is much reduced due to inflationary spirals.
When it comes to, say, coal fired power, the design life may be 25 years. Think of that as an expected minimum life, during which the asset must be paid for. It is not unusual for ways to be found to keep 25 year old power stations in service for a further 15 or more years, which are essentially the icing on the cake, but bring with them need for capital injection for plant improvement projects, increased maintenance and reduced efficiency by comparison with alternative new, ultrasupercritical coal powed station. Same fuel, two different options.
Try the example of working out using standard economists’ tools the present value of an income stream of, say, $100 per year at 5% over 20 years, then 30 years, 40 and 50. Then repeat using a discount rate of 10%.
The discount rate is more significant than the term, because the value today of a dollar earned 50 years down the track at 10% is (1.00 – 0.10) raised to the power of 50 = 0.57 cents. At a discount rate of Japanese or current US magnitude could be assumed for the whole of the asset’s life, we might use 1%, in which case present value of $1 in 50 years is 61.11 cents. Since 1% discount rates are not expected in the real world, the real world value of income generated 30, 40 or 50 years down the track is negligible in comparison with other costs and risks.
Extending the life of a planned investment is thus not very attractive at the planning stage, especially because the plant may well fail to reach the extended life. If it has blown up or burned down, then the anticipated cash flow will cease. The bet will have been lost.
By comparison, when the investment reaches 25 years and is still operating satisfactorily and technological advances are possible to economically extend its life, then life extension can be very attractive. Just don’t assume in Year 1 that this will always be possible.
I was thinking of something on a much larger scale. I was thinking of something like wall street, a clearing house, but non profit, and it woule be for the benefit of people who want to invest in real projects, not just the gambling operation we have now at wall street. So this wall street clearing house would match projects with interested end use customers where the customers receive the final product instead of cash. Financing a large nuclear plant with a million small customers should not be a problem if the right type of clearing house is set up.
David, with such low clearing prices, how are new capital intensive projects financed and paid for? How are customers charged for the capital cost? If the capital costs are put in a rate, what is keeping that customer from choosing another provider that doesn’t have the capital costs in their rate base? Do customers in Australia have a choice as to who will provide their power or are they stuck with one company that supplies all their needs? Maybe the market in Australia is just used so the utilities can buy and sell power. If so, that would be nearly equivalent to an economic dispatch.
JB, @ 7 November 2011 at 8:36
That’s an informative post with many interesting thoughts and relevant specific detail.
I agree with much of what you say about what has gone wrong with ad hoc approach to energy policy.
I like your Proposal #2. However, I think the Federal government should fund it, not AEMO. If AEMO funded it the cost would have to be passed on to the electricity consumers in higher rates. It is a social and policy obligation that the Federal Government should fund, IMO. Does AEMO have the project management expertise that would be needed?
I’d suggest my earlier proposal is very similar to yours. I refer you to my fairly ‘SMART’ proposal here: http://bravenewclimate.com/2010/01/31/alternative-to-cprs/ . I believe is covers most of the bases, specific actions, time-line, was realistic and achievable at the time (except for politics) but now delayed. I believe this proposal provides some more detail about the steps and the time-line that would be required.
Regarding Proposal #1:
I agree with the objective. However, I wonder if the suggestion I made last year and reposted up-thread @ 5 November 2011 at 8:52 AM , might be give us a quicker start, and have more authority because it would be seen as independent (if the Terms of Reference are not biased) than your Proposal 1. Perhaps elements of your Proposal 1 could follow.
I’d suggest the Productivity Analysis would need to be a precursor to Proposal #2.
I’d also refer readers to the lead article of the “Alternative to Carbon Pricing” thread. http://bravenewclimate.com/2010/01/31/alternative-to-cprs/ Much of what John Bennett’s has proposed was covered in the post, including a detailed time line and, especially, how to progress with educating the population. I remain convinced this post is basically the way we should proceed, although I now believe we’ve lost about 7 years, largely due to the CO2 tax and ETS legislation and the political delay it will cause while it is being unwound. I doubt nuclear can be pushed by either side for at least the next two and probably the next three elections.
I’ve had a quick scan of the PwC report. I don’t think much of it. It seems to be about trying to find more ways to build renewable energy and hide the true costs. For example, they propose to rob from the pension funds of those who have no chance to save or earn to make up for the stolen funds:
We should not be making pension funds invest in things wiser investors will not touch. If an investment is sound, the pension funds will invest in it without “encouragement” from government. This proposal seems like another intervention designed by bureaucrats in Brussels. They have little understanding of investing and finances, just like our own Treasury Department displayed so convincingly with the Resource Super Profits Tax fiasco.
Jani Martikainen, @ 7 November 2011 at 11:34 PM:
I have no more expertise in this that anyone else here. Here is my take on this.
When defining the terms of reference for the LCOE study EPRI undertook, the contracting agency (DRET) and the consultant (EPRI) would have agreed what factors to hold constant in the analysis and which should be varied. Considering the audience and the purpose of the study, I expect they agreed to keep as many factors constant as they reasonably could. I expect they decided to hold Capacity Factor constant at 85% for the baseload technologies, and “book life” constant at 30 years.
Someone who is more interested in nuclear than the other technologies might approach the LCOE calculation like this:
Plant life for nuclear = 60 years
Plant life for Wind = 20 years
Nuclear has two or three major refurbishments which have to be included
Wind plants have to be constructed three times.
The future capital costs are on a discounted cash flow basis.
Changing the life of the NPP from 30 years to 60 years and leaving all the other EPRI inputs the same, the LCOE changed from $144/MWh to $135/MWh (in 2011 US$)
John Bennetts,
I think you are confusing the issue when you mentioned inflation. In most cases LCOE analyses are reported as “real” or “Constant” dollars not “current” dollars. So the effects of inflation are excluded.
The reason that the value decreases with time is because a $ now is more valuable than a $ next year, even if there was no inflation, because of what you can use it for in the meantime, such as investing it and getting a return on the investment.
That is how I understand it. Someone correct me if I have it wrong.
Gene Preston — Here in the Pacific Northwest no new highly capital intensive projects are in planning AFAIK. The only generators being built are wind turbines [with some form of tax incentive or subsidy attached] and CCGTs. When hydro turbine/generators wear out and have to be replaced (as is beginning to happen to the legacy hydro), the costs are added to the consumer rate base; I estimate the average cost of electricity to consumers around here will grow by about 4% per year.
There is no choice of retail utility company possible around here and they buy from whatever supplier they wish [subject to utility regulatory commission post-review for ‘best’ prices]. The only exception is for ‘bleeding greens’ who want to pay extra for wind power; presumably the retail utility passes that extra to the participating wind farm(s).
The various hubs are used to set future and current prices for the relatively small proporation of power not under long term contract; so-called spot prices.
I don’t know how all these matters are treated in Australia. All I know is that the academic power engineers down the hall have high regard for the Australian ISO.
LCOE: So-called constant dollars are ordinarily assumed although this is not necessary. For a generator which is expected to last longer than the life of the mortgage, LCOE needs to be appropriately averaged between the mortgage life period and the extention; doing that properly is less easy than one might think.
For example, suppose a Westinghouse AP-1000 at a particular site has all-up capital costs of US$5100/kW, including finance charges during construction. Using otherwise US standard figures the LCOE during the 30 years of the mortgage is US$0.099/kWh. The difficult part is determining that the LCOE for the following (presumed) 30 years of useful life is US$0.053/kWh giving an average LCOE of US$0.076/kWh [which is the justifying LOCE for VC Summer, now in pre-construction as this phase might be called].
PL:
Proposal #2. I’m not surprised that it is more attractive to you. Me, too. I agree that the Federal Gov’t could/should fund it – the reference to funding via AEMO was included for variety and from a purist’s point of view. Energy planning org should pay for energy options planning… to a point.
Quite likely, in practice AEMO would have an input and kick in some costs by way of staffing and studies, as well as their very well established competion and industry regulator role. AEMO are indispensible partners.
Agreed about the social objectives. In a way, it’s a bit like the early days of the Snowy Mountains Authority, during which the project first took shape. NSW, Victoria and Commonwealth shared in this, mainly due to land ownership and other jurisdictional matters. The states need not be co-opted into the NPP effort, at least not as lead partners.
“Does AEMO have the project management expertise that would be needed?” In a word, No. However they are not without very strong resources in areas including legal/regulatory, economics and engineering project assessment. Whoever runs this thing would need to build a project team. Governments of the 21st century no longer have the depth and number of staff with suitable experience. Assembling an adequate project management team must be done with great care, because any weakness in this area will lead to domination of the project by the strongest player – possibly leading to cultural ambush of the project by the potential head contractor(s).
I will re-read your references this evening.
I intentionally avoided considering timeline, because until there is a map for the journey and a vehicle, the velocity cannot be determined. My experience has been that projects with too tight a timeline are at most risk of failure. NBN, anyone?
I will cogitate more about the early role of AEMO. If the project’s Champion is a Federal Minister, AEMO probably have a central role to play during the investigation and options study stages. Handover to a broader project team at that stage may be appropriate, to ensure that a balance is struck between the need for boffins with open minds early and the need to replace the boffins with more experienced delivers of projects once things take shape. Think of defining the scope before handing over to a conventional engineering design and delivery operation, leading to the Alliance which I mentioned before. AEMO would then probably be part of the Principal’s/Owner’s team, rather than within the Alliance team, as also representatives from relevant government departments and ANSTO, etc (but not regulators).
In the final washup, the project is not huge. A couple of NPP’s is a large but not exceptional, undertaking. For example, Bayswater Power Station in NSW had a peak on-site workforce of 2400, plus another 200 or so Owner’s staff. Project delivery has to be separated from management of scope and change, otherwise the tensions between scope, quality, dollars and time will be lost and one will prevail to the detriment of the other three. The Project Manager (responsible to the Champion) must not become the Alliance Manager, but his organisational equal.
For the above reasons, I would not recommend using a single consultant to lead project definition and delivery. Too often, that path leads to tears, but perhaps I am showing personal bias. Besides which, if things start going wrong between an Owner and a super-consultant, the consultant holds too many cards and the Owner too few.
The “Alternative to Carbon Pricing” thread is frustratingly slow to load so I realise most readers will not follow the link to that thread. I’ll extract the main part I was urging people to re-read and post it here (an hope the Moderator will allow this). Although it is nearly two years old I believe it is still mostly what we need to do. I suggest the general thrust of this is consistent with what John Bennetts suggested @ 8 November 2011 at 9:31 AM
Alternative to the Carbon Pricing
See preceding section here: http://bravenewclimate.com/2010/01/31/alternative-to-cprs/
Implementation Details
This policy:
1. will cut Australia’s GHG emissions from electricity generation by 8% of current levels by 2020 and by 80% by 2050;
2. is by far the least cost option to cut emissions; and
3. will give the least cost electricity of options to cut emissions.
How will this be achieved?
1. Coal power stations will be decommissioned at the rate of 1.4 GW per year.
a. They will be decommissioned as they reach their retirement age,
b. together with a small component of government buy back in a “Cash for Clunkers” scheme
2. They will be replaced with (mostly):
a. Natural gas generation until 2020, then with
b. Nuclear and efficient Combined Cycle Gas Turbines (CCGT) until 2025, then
c. Nuclear (mostly) to 2050.
3. Coal with Carbon Capture and Storage and geothermal may play a role if they become commercially viable.
4. Wind and solar power will have only a minor role unless major technological advances are achieved
5. Some Pumped-hydro will be built using existing dams – for example by connecting existing dams in the Snowy Mountains.
Implementation.
1. A project like a modern version of the Snowy Mountains Scheme initially (to about 2025) to get it through about the first 15 years;
2. A Sir William Hudson type person in charge;
3. “Early Wins” – Establish research facilities in at least one major university in every state; and
4. Research – A significant component of the research will focus on how to implement nuclear energy at least cost in Australia. [For example, how will we avoid the political, NIMBY, regulatory and bureaucratic problems that have raised the cost of nuclear in USA and EU.]
Level playing field for electricity generators
What would be a genuine level playing field for electricity generators”?
1. Remove all mandatory requirements (e.g. the Mandatory Renewable Energy Targets)
2. Remove all subsidies for electricity generation
3. Remove all tax incentives and other hidden incentives that favour one generator technology over another
4. Ensure that regulations apply equally for all types of generators. Set up a system to allow electricity generator companies to challenge anything that is impeding a level playing field
5. Emissions and pollution regulations must be the same for all industries and should be based on safety and health effects on an equal basis.
Policy implications of “Emission Cuts Realities – Electricity Generation”
Some policy implications of the paper: “Emission Cuts Realities – Electricity Generation” (Lang, 2010)
1. Mandating renewable energy is bad policy
2. If we are serious about cutting GHG emissions, we’d better get serious about implementing nuclear energy as soon as possible
3. If we want to implement nuclear power we’ll need to focus on how to do so at least cost, not with the sorts of high cost regimes imposed in USA and EU
4. We should not raise the cost of electricity. We must do all we can to bring clean electricity to our industries and residents at a cost no higher than the least cost option
5. Therefore, ETS/CPRS is exactly the wrong policy
Schedule
Following is a proposed schedule for Australia’s federal Government, noting that our next Federal budget is in May 2010.
May 2010 – Federal Budget contains funding for the following to be implemented during 2010-2011:
1. Establishment of a modern version of the Snowy Mountains Authority. Terms of Reference: to implement low emissions electricity generation in Australia such that electricity costs less than from fossil fuel generation.
2. Funding for nuclear engineering faculties in at least one university in every mainland State
3. Funding of research will be largely for the social engineering aspects of implementing nuclear energy in Australia at least cost.
2010 – Government announces policies:
1. to allow nuclear energy to be one of the options for electricity generation;
2. to remove all the impediments that favour or discriminate one generator system or technology over another;
3. that 20% of emissions will be from low emissions generator mix by 2020 and 80% by 2050. A ‘low emission generator mix’ is a mix of generators that can provide power on demand and meet the emissions limits that will be phased in and become more stringent over time. For example, the limit might be 200 kg CO2-e/MWh in 2020 and 10 kg CO2-e/MWh in 2050. The rate would decrease progressively over time – but not necessarily linearly. The rate does not apply to a single generator. It applies to a company’s mix of generators. The 2020 limit could be achieved by a mix of 50% high efficiency CCGT combined with 50% of one of the following: nuclear, hydro, biomass, geothermal, solar thermal with its own energy storage. Wind cannot meet the 200 kg CO2-e/MWh for the reasons explained here: http://bravenewclimate.com/2010/01/09/emission-cuts-realities/
4. to buy back some old coal generators at a fair price in a “cash for clunkers” scheme
5. to conduct first public awareness forums throughout Australia.
2012 – Government announces policies to:
1. allow nuclear power plants to be established in Australia and under what conditions;
2. allow States to bid to host the first nuclear power station and the conditions for selection of the state – this will include a time frame for site selection to be complete by 2013 (I know its fast, but if its urgent we need to get on with it!). In the absence of states bidding and agreeing to meet the schedule the first NPP will be build on Commonwealth owned and controlled land.
3. Establish arrangements with IAEA to act as our Nuclear Regulatory Authority until we are ready to take over.
2013 –Source selection starts for our first four or five NPPs
2014 – Contract awarded for first four or five NPPs
2015 – Construction begins
2019 – First NPP commissioned.
2020 – Second NPP commissioned, and so on,
I suspect the reality is we’ve slipped another seven years from these dates as a result of the government’s determination to legislate the CO2 tax and ETS and showing no signs of dumping their anti-nuclear policy
JB @ 8 November 2011 at 12:53 PM
I am reading your comment after I posted my extract from the “Alternative to Carbon Pricing “thread. I am hoping we may able to combine our proposals – what’s good out of your two proposals and my two (Productivity Commission suggestion and the extract from “Alternative to Carbon Pricing”).
I think we have to do much better than that. Ministers come and ministers go. And governments come and go. If this is tied into politics, it will be a long slow road. I am thinking of a real engineer leader such as:
• Sir William Hydson – he built the Snowy Mountains Scheme and managed all the politicians for abut 25 years.
• The Adelaide guy (bless his soul 🙂 who spent most of his life dedicated to getting the telegraph line built from Adelaide to England.
• The engineer who built the Panama Canal.
• Many other examples. It will need a leader from outside politics.
Actually, come to think of it, I reckon one guy who ticks nearly all the boxes is Ziggy Switkowski. He ran Telstra, and has the logistics and political skills.
You’ve gone into a lot of detail about responsibilities and roles. There is a lot to program management and probably that would take us into too much depth at this stage. If we can’t find a way to make nuclear economically viable its not going to happen. At the moment we are a long way from them being viable. I feel many people are going to have to be prepared to give up on some of their very strongly held beliefs before we will make much progress on this.
Thank you for you responses. I think I understand the concept of “book life” better. So basically for LCOE it doesn’t mattter hugely whether it is set at 30 or 60 years. On the other hand, for long term construction and other requirements (in order to decarbonize the energy system) the expected life time matters more, since some choices would have to be rebuild before we have yet finished the task.
@Peter:”Is TVO one of many electricity companies that are competing. If not are there competitive pressures to keep electricity industry efficient and low cost, or is price controlled by a regulator?” There is competition and shareholders in TVO compete also among themselves since they usually own generating capacity also outside TVO. Also, finns, swedes, norwegians, and danes have a common electricity market so the players in other nordic countries influence the prices here. My own contract for electricity is with a norwegian company, heat probably comes from the local utility (I rent a place so I am not sure which one), and for the grid services I pay to whatever company owns the grid here. The cost for grid services is, I think, regulated, in order to ensure competition.
Jani Martikainen,
Thank you for that information. That sounds like an excellent arrangement. Trust the Finns (and the Scandinavians).
Peter, “Trust the Finns (and the Scandinavians).” Be careful with such statements. I can assure you that we have our share of silliness as well. I suspect that the amount of woolly thinking is roughly constant across nations as long as we take the average over few years:-)
Right now Nordics on average enjoy much lower electricity prices than germans, but when EU electricity markets integrate things will change. Right now there is very little transmission capacity to Germany, but at some point the price gradient becomes too steep to resist. Once the transmission capacity is there, the prices here will approach those in central Europe. So many things that affect us depend on decisions done in bigger markets. Even decisions regarding future NPP:s (2 new ones have been politically approved) might have to factor in whether or not they are in a position to sell their production to Germany.
Jani Martikainen,
David Benson, thanks for the Pacific NW view. We have the same thing going on here in Texas except our wind program is more aggressive by building enough new socialized transmission to double the wind from 9000 to 18000 MW in a system peaking at about 65000 MW in the summer and we have nil hydro. What the large influx of wind has done is caused the builders of gas to take pause on their new gas plants because the wind eats into their revenue stream. So even though wind needs gas for backup, the wind is killing the economics of gas if you can believe that. There is no way to finance high capital cost solar and nuclear in this market. I’m also interested in how Australia works.
David, the problem I have with using only the time value of money in assessing generation options is that LCOE puts too much emphasis on the current and not enough emphasis on the future. LCOE is almost completely blind beyond about ten years if the discount rate is fairly high. So lets say that we want to have zero CO2 in 50 years. If we just use LCOE to make desisions today about solar, nuclear, wind, coal, etc. We will always decide that coal is cheapest, to heck with the future, etc. But that is not the long range objective. Just relying on LCOE alone is leading up down a path of destruction on this planet. I now prefer to give equal weight to all time periods, i.e. just use a discount of 0% and give the same weight to future dollars as current dollars so that the generation mix of the future can reveal itself. If you do this then your earlier comments about wind having to be built three times for each nuclear plant life reveals the real cost of wind which is much higher than nuclear.
Lets say your kids take a view of history 20 years from now. They look back at your decision based on the time value of money in which we today decided we could not afford nuclear because the LOCO was too high. Those kids 20 years from now will have a pathetic energy short world on their hands and wonder how could we ever have made such a self centered short range vieww of the world so as to deny them a future. We today are depleting oil gas coal, and are raising the CO2 level to dangerout levels. Lets face it, the real evil is relying almost entirely on the time value of money at the detriment of our future kid’s standard of living. LCOE causes us to not be able to see into the future beyond our noses. LCOE used by businesses today is an evil force in itself that is leading us into destroying the planet.
The NREL calculator has an overall cost escalation parameter with the default rate set at 3%. That doesn’t handle a step jump to a flat carbon tax in the middle of the period. With gas prices in Australia even industry insiders expect 5% arithmetic cost increase
http://www.canberratimes.com.au/news/national/national/general/gas-prices-to-double-in-20-years-as-demand-explodes-santos-predicts/2342581.aspx
However on gas I’d ask how will we make urea fertiliser when the world has 9 bn people? How will we power farm machinery when there is no diesel and very little gas? Today’s children should still be alive when this happens. Economic theory assumes when a key resource hits price $x a satisfactory substitute steps in to fill its place. we’ll soon see.
Today a politician announced that the carbon tax bills had passed into law. He said as a result two new gas fired power stations would be built. He didn’t say
– they were additional to coal, not replacements
– it doesn’t jibe with 80% CO2 reductions promised long term
– other parts of Australia don ‘t have the luxury of new gas plant.
It’s all piecemeal and fails to see the bigger picture.
@Gene: That is a good point. LCOE does not include the (discounted?) costs caused by fossil fuels. Those costs are not shouldered by whoever invests in fossil fuels. In this sense it is incomplete measure just like GDP is not always a useful measure of nations well being. (Not a useless measure, but incomplete.) Unfortunately I guess the way things are financed today force this shortsighted behavior. Actually, if I were a consumer of electricity and a utility asks me to invest in a bond which is used to finance NPP for example I would be more than happy to get say 5% interest or even less. I see no relatively safe place for my savings that could offer that. Where this disconnect between typical discount rates and reasonable returns in the current market environment come from, I do not understand.
Regarding the discussion about what capacity factors, discount rates, “book life” to use for LCOE calculations, I came across this recent report. http://www.iea.org/papers/2011/costperf_ccs_powergen.pdf It is about CCS costs and compares eight LCOE analyses. The key input parameters are summarised in Table 2. The range of values used in the eight studies are:
Discount rates = 9% to 10%
Owner’s costs = 5% to 25%
Capacity factor, coal = 75% to 85%
Capacity factor, natural gas = 75% to 95%
Economic life, coal = 20 to 30 years
Economic life, gas = 25 to 30 years
Construction time, coal = 3 to 4 years
Construction time, gas = 3 years
Contingencies with CCS = 5% to 30%
Table 10 gives capital cost, LCOE, relative LCOE increase for CCS = 39% to 63%
LCOE with CCS = $102 – $107/MWh
LCOE increase = $29 – $41/MWh
Cost of CO2 avoided = $43 – $80/t CO2 avoided.
The caption below the Table 10 includes this which will be of interest given earlier discussion on this thread:
A paper by Alstom delivered at the POWER-GEN Europe Conference, 7-9 June 2011, Milan, Italy, “Cost assessment of fossil power plants equipped with CCS under typical scenarios” does not appear to be accessible on the web. The abstract says:
Figure 18 summarises the LCOE for nine different low carbon technologies over the 2011 to 2016 period. Eyeballing from the chart I get the following for the average min and max LCOE for each, in € / MWh:
Hard coal with CCS = 86; 80; 110
CCGT with CCS = 65; 50;80
Nuclear = 47; 45; 65 (the lowest of the average for the low carbon technologies)
Hydro = 50; 15; 90
Geothermal = 60; 60; 70
The others are: Wind onshore, wind offshore, solar thermal, solar PV. All are higher cost. Solar thermal = 225; 150; 265.
John I saw your comment:
However on gas I’d ask how will we make urea fertiliser when the world has 9 bn people?
I went to a talk the other day about a new CCS plant in West Texas that will send the co2 to oil producers to inject to increase oil production. A by product of their process is urea fertilizer. And it produces a lot. I think about 1/4th of the US use of this fertilizer. One concern by the plant owners is that it will produce too much urea and depress prices.
Gene, @ 8 November 2011 at 8:15 PM
Both sentences are wrong.
Firstly, LCOE is not leading us down a path of destruction. As explained in a comment up thread, the LCOE method is also used to calculate the LCOE with externalities included or CO2e price included.
Secondly, arguing that rational people would apply a discount rate of 0% is nonsense. If that was the case, you could walk into a car dealer, buy a car and the terms would be “pay whenever you like. You can pay for it now, of in a year or 10 years of 100 years time. If you choose to pay at a future date instead of now, the only added cost is the rate of inflation”. So he sod you a car and you don’t have to pay for it. How nuts is that?
GP I’m using urea as a generic term for nitrogen fertiliser including nitrates, ammonium salts like diammonium phosphate, anhydrous ammonia and urea. Wikipedia opines that world population is a third more than otherwise due to nitrogen fertiliser. That’s now so that dependence can only become stronger.
The key point is that we need to conserve some hard to replace resources like natural gas for the long run. On TV one of the mayors in Queensland’s coal seam gas growth areas said gas fired power stations were ‘sustainable’. Huh? Like the Brits in 2011 the world as a whole in 2050 will look back at how we squandered so much gas, notably baseload power when there is an alternative.
Peter Lang and all the others,
thank you – this has been a very enlightening discussion. Unfortunately I don’t have the time right now to follow all the links, but I’ll save the discussion for future reference.
As far as the “Mankala principle” of tax-free electricity I mentioned goes, you should know that it’s far from being generally appreciated here in Finland. There is a view – strongly held by certain commentators of Greenish bent, but not exactly uncommon nor unconvincing – that the principle favors heavy, energy-intensive industries while shortchanging less energy intensive businesses.
I’m no expert, but I strongly suspect that its original formulation in 1968 was somewhat influenced by the demands of the paper industry at the time. A common critique leveled against NPPs here is that they are artificial life support for old, energy-intensive manufacturing industries we should get rid of anyway. We’re actually behind most other European nations in that curve, as we still have a significant manufacturing sector (paper and metals mostly).
That and some admittedly poor policy decisions over the years also mean that our carbon footprint is far from ideal. It’s over 12 tonnes per capita per annum, far higher than even Denmark’s, and one of the highest in Europe. I suspect it will drop once new NPPs come on-line, but as much of the emissions are from oil (45%) and from coal (39%), much of which is burned in municipal CHP plants, the reduction won’t be that impressive. We’ve basically locked ourselves into “efficient” CHP plants, and the alternative fuels are either peat (very bad) or wood-derived biomass (not as bad, but limited).
This lock-in to what seemed an “efficient” solution at the time is something I worry about. I think I agree with Jani-Petri in that optimal solutions at any one time may turn out to be suboptimal in the long run.
Peter the zero discount rate does not mean you would pay for the car at any time in the future. Even with a non zero discount rate would the car dealer sell you the car if there were a 10% annual interest and you agreed to pay 1.10^30 or 17.5 times more for that car 30 years into the future? Would he sell you the car? No. So your example does not make sense either.
LCOE is leading us down a path of destruction because we are blinding ourselves to whats in store for us 50 years in the future. For example at 10% per year, a dollar 50 years from now is only worth 1/117th its current value or about a penny. So we see those huge expenses in the future just dwindle to no concern at all today, because we know that we will be able to pull a magic want out of the hat and walla, the LCOE analysis will take care of us at some point in the future when all hell is breaking loose.
Here is an idea for you to mull over. The doubling time for an exponential function is 70 divided by the interest rate per year. So if we used a discount rate of 10% we are implying that we have just 7 years to solve a problem. If we used 7% discount rate we have just 10 years to solve a problem like CO2. Lets say that it will take 70 years to solve the CO2 problem. We should be using a discount rate of just 1% in our studies to make decisions on a 70 year time frame.
Gene Preston — LCOE is a generally accepted method of comparing the cost of alternate methods of generaation. It is overly simple in that other factors such as reliability are not directly included and as you previously noted these may be dependent upon the existing grid.
I’ll have to ponder for some time the idea that typical interest rates discount the future overly rapidly. I suppose I’ll attempt to see what various academic economists have written about that.
DBB using the LCOE formula given here
http://en.wikipedia.org/wiki/Cost_of_electricity_by_source
but for constant output and annual cost some sensitivity analysis suggests the results are not strikingly different.
For example rather than discounting for years n = 1,..50 by the weight [(1 + r) ^ -n] I consider the case of no discounting (r = 0) years 1,..20 then ignoring (r = ∞) years 21,…50. For r = 0.1 or 10% and constant annual cost 10c per kwh I get
truncated no discount case LCOE = 10c
full term 10% discount LCOE = 11.7c.
No biggie if my calcs are correct. But consider the case the world has effectively run out of gas (for example) by 2050. Do we want our descendants to starve and freeze? Discounting seems to assume we make hard headed decisions now and magic will happen in the future.
Hi, Peter L.
I agree that ministers come and go, but your four examples are all flawed. Maybe we need to dig further to find ideal examples. It appears that we do agree, at least in general, that above the project team must be an enabler, the person who I have titled the project’s champion.
Sir William Hudson was a magnificent fellow. Long after his retirement, he used to speak annually to a group of engineering undergrads, of which I was one. However, the project had ministerial support from 2 States and at Federal level who provided the support, the enabling legislation and the funding. He outlasted them all, of course.
The engineer who first tried to build the Panama, Frenchman Ferdinand de Lesseps, went bust on the project. The project was constructed by the US government, using primarily directly employed staff from various countries and under the management of a series of three commanding engineers, the last of which, George Washington Goethals, lasted longest and completed the job was was not the designer. The project’s enabler was US President Roosevelt, who forced the creation of the nation called Panama which was carved out of Colombia after the Spanish-American War. Its constitution includes a much-argued provision for the USA to occupy, rule and control the Canal Zone which splits the small nation in two, for ever. If not for Roosevelt’s championing of the project, including by being the first President to leave the US whilst in office to visit the Canal Zone, the canal could never have been constructed. (Ref: Julie Green “The Canal Builders”, Penguin, 2009.)
I would add General Sir John Monash, a most remarkable linguist, civil engineer and general who was the first and perhaps most successful boss of the State Electricity Commission of Victoria, the SECV. A most remarkable man, but again, he was appointed to this nation-building role by politicians who supported him with legislation and funds. That project’s commencement can be traced to enquiries and legislation in 1917 and 1918. Sir John Monash’s involvement as Chairman and CEO dated from 1920.
Think also of Kennedy and the Appollo project.
Consider also the Sydney Harbour Bridge, which was the brain-child of JJC bradfield, but was designed and substantially constructed by British corporations. It took Bradfield 10 years, 1912 to 1922, before he obtained the legislative support and finance with which to proceed. Bradfield’s proposal was superb, as also his abilities constructing railways and the SHB. Until 1922, the project lacked a Champion.
The first NPP in Australia will need more than just good or even great project management, it will need a Champion to provide the public and political will, the necessary legislation and the finance.
That is why I view political will as being the highest hurdle preventing construction of an NPP in Australia.
I’m working slowly on a review of economic factors behind the high projected cost of nuclear power in Australia compared with USA, as discussed upthread. A trip away has intervened… perhaps late next week.
Jani Martikainen, on 8 November 2011 at 9:20 PMLang, several hours later:
Peter’s comment was to the effect that externalities are/can be included in LCOE calculations.
The notion of externalities is an economist’s concept of those matters which represent costs or benefits but which are outside the analysis. Thus, unless externalities are specifically introduced, the default situation is to ignore them.
I suggest that those not familiar with the terms “externalities” and “economic commons” check Wiki or an economics text or site before proceeding.
It is exactly damage to economic commons which contributors, including Gene, are attempting to value and thus to prevent. Gene, at first reading, appears to say that all damage to the commons is anathema and must be avoided, especially the commons known as the atmosphere, or the climate.
Placing a value on damage to the economic commons and placing a value on human subjective value gained or lost are the classic externalities. There is no easy answer, no simple way to arrive at a universally agreed valuation.
I am sure that Barry Brook will have run across several red hot attempts to put a value on environmental degradation. These include (warning: amateur at work!) costs of adaptation (eg walls to keep rising tides out, or cost of moving infrastructure upslope), economic loss (eg crop loss, cyclone damage, fisheries destruction) and more.
However, once externalities have been identified, quantified and evaluated, their costs and benfits ARE able to be included in economic evaluations.
What I disagree with is blanket “I don’t like it” type argument which is then followed by “then I will ignore/outlaw that factor”, as exampled by current inability of the basic LCOE procedures to consider future climate change and the response, from Gene, that he will thus ignore the economic reality that, in a world where the value of money changes with time and ignore these changes, which are real and measurable.
Gene’s response is akin to hiding one’s eyes behind one’s hand. That which is no longer seen is still real.
Regarding cash flows expressed as constant dollars Vs discounted cash flows, these terms are defined in Wikipedia and elsewhere.
The simple explanation is that constant value dollars have been adjusted to base date to adjust for inflation.
Discount rates may be thought of as being the annual cost of money borrowed, expressed as a percentage. The rate must allow for borrower’s costs, lender’s margin and fees and charges attached to the loans. Most corporations add a further impost onto the discount rate which must be used for project evaluations, perhaps a bit like an internal rate of return for the capital used – I have worked with figures from 1% upwards for this additional margin, but never zero.
In Australia during the past decade or so, the annual rate of inflation was typically about 3%, whereas the discount rate for housing loans has been around 8 percent. They are not the same animal. That explains the missing 5%.
John how would you perform the time value of money if inflation exceed what you can earn on an investment. I subscribe to Stansbury who says that we will soon see very high inflation in the US. I have talked with utility executives who are buying solar power with an inflation clause in the contract. I query them about that expected 2% per year inflation they are assuming and they assure me the Feds will be able to hold down inflation. I just shake my head and say to myself, you are a fool indeed. We are going to see very high inflation soon. Those nuclear plants built before the high inflation are going to look like really good investments. Your LCOE figures are not capturing this future which I have a lot more confidence will happen than the other possibility, which is we will be able to keep doing business as usual indefinitly into the future. We are all in for some really rough days ahead as oil peaks and environmental science keeps improving and telling us we are destroying the planet. These things are going to cause really high inflation at some point.
DBB:
Because the discount rate is always larger than the inflation rate, evaluations based on the time value of money at discounted rates will always appear to place a higher value on early cash flows when compared to evaluations calculated using inflation-adjusted constant dollars.
The subjective experience will be the same.
The difference, as explained above, is the economic friction due to lender’s margins and fees and cost related to the actual loans. Normally, added to the discount rate is a fudge factor determined by the CEO, CFO and/or the Board, which will always push the project-specific discount rate up further.
Remember: An inflation rates is measurable – a statistic.
A discount rate is a tool used for financial comparisons and may be adjusted up or down to suit the owner’s preferences, his perception of risk and desire to proceed. It is just a number. That is why evaluations are usually carried out using several different discount rates – otherwise known as determining sensitivity to discount rate.
If a company is used to making 20% pa on its investments, it might be entirely rational to require a discount rate of (20% plus costs), say 22%, regardless of the current or expected inflation rates.
Consider also that there are many different inflation rates operating in any given community at any one time. The rates of inflation for labour, consumer expenditure, electricity, transport costs and many other things are different. Selecting an appropriate estimated future rate of inflation for your constant dollars is not as easy as it might appear at first pass.
Gene:
What matters is not today’s inflation rate or tomorrow’s, which as I explained above doesn’t really matter in respect of making decisions to commit funds. What matters is the discount rate which the corporation perceives as being appropriate to finance the job, after all costs and risks related to arranging finance for that cash flow.
A corporation risking funds has additional tools, such as hedging, which can be applied to the anticipated cash flows. These facilities cost quite a bit.
Under normal circumstances, a hedge will cost several percentage points on the amount needed, compounded throughout the period of the loans.
The simple explanation of the result is that the cost of capital becomes the cost of (hedged) capital, which may move from 8% to 10% in order to transfer this risk to the lender and away from the corporation doing the borrowing.
If a single project represents a threat to the corporation’s existence should funding fall through, then the corporation would be well advised to take the insurance (hedged loan), pay the money, and include the costs in the discount rate used for evaluation of the project in the bid phase.
If, at the other end of the scale, the amount involved is relatively small and the perceived volatility of the economy low, then these would tend towards the corporation deciding to carry the risk alone. Whether they still adjust the discount rate in response to perceived future increased in input prices or of inflation more generally is a management decision, typically taken outside the project team.
I doubt very much if any corporation large enough to contract to construct power generation facilities operates on a simple model when it comes to project finance. Each project’s financial risk matrix is just as significant as many other variables, eg labour rates of inflation, or sensitivity to long lead time items, which are perhaps more easily comprehended. The corporation’s treasury department and that of the purchaser will very carefully examine these aspects of the project, from the perspectives of contractor and client. The list of risks and allowances on a large long-term project can easily amount to 30% of the budget estimate.
For example, not too long ago, I was asked to take over project management of a job estimated at $63M, where the budget was only $52M. By addressing and minimising risks, from both the supplier’s and the client’s perspective, the project was re-scheduled to complete a year later but it came in at $43.9M all final, all done.
Where was this money found? Risks were identified and managed.
Design was completed before tendering.
Just-in-time design needs large contingency factors for unknowns.
Large and long lead time items were pre-purchased, thus enabling construction contracts to be let later and based on final designs.
Because the design was completed, the previous 8 on-site contracts were rolled into one, hugely reducing on-site supervision and quality costs to the client, as well as cordination snafu’s.
And so on… 1/3rd knocked off the cost of an award-winning project, mostly achieved by managing commercial and design risks.
I guess that this answer may not fully convince Gene, but essentially the discount rate which a corporation adopts will include allowance for the types of perceived risk, eg of future inflationary pressures. Perhaps the discount rate can be thought of as the price of money to the project – the internal price at which the corporation is prepared to put money on the line next year and the ones after. It is thus divorced from the current rate of inflation, estimates of future rates of of inflation and the estimated costs of borrowings by the firm, which are only several of the inputs into the final determination of a discount rate.
I have read recently that AEMO, the Australian energy market regulator, is re-thinking billions of dollars of high voltage transmission projects because of concerns that the asset owners are profiteering from differentials between the real net cost of capital and the discount rate which was agreed to by the Regulator during the project approval phase, which is where those (indexed) costs which may be added to retail tariffs are approved. Lawyers and economists are getting richer and fatter as the dabates rage… there are literally billions of dollars at risk, just in southern and eastern Australia, a market population of roughly 20 million people.
Sorry, Moderator… this has been another marathon post from JB.
MODERATOR
It’s not the length that matters, it is the content. Great content but please remember to supply the refs/links where available e.g.
Gene, @ 1:52pm:
1. LCOE is not an adequate tool for project approval, whether as client or constructor. It is used for comparisons only, as a way to compare competing projects, using a consistent set of assumptions regarding such matters as discount rates.
2. Discount rates can be varied and often are for comparison purpose. That way, projects which have high up front capital costs can be compared fairly with competing projects, some of which have low up-fronts but high O&M.
3. Capturing the future…
It is possible to input varying anticipated costs and expenditures into financial models for specific projects and to run “What if?” scenarios endlessly, however this quickly reaches beyond the purpose of LCOE tools.
Smarties can and will use LCOE models over various time ranges and discount rates to espimate outcomes from such things as a step change in discount rate at Year 10, or an increase in fuel costs at rates which are higher than the discount rate or general inflation rate, but this quickly becomes futile because project-specific costs and market factors will quickly swamp any apparent precision gained thereby. I think of the LCOE as a way to tell whether to buy a new car or an SUV, and how much to budget. What it cannot do is tell me what the actual price of the vehicle will be, or what brand and model. It can thus narrow the range, but not make the final decision.
John you said an inflation rate is measurable – a statistic. But this is only true in hindsight. Everyone is assuming low inflation rates will continue. Herein lies a trap. If you knew that energy shortages would trigger high in flation in the not to distant future, you’re LCOE calculations would show completely different results.
The second mistake you are making is implicitly assuming corporations will save us through the market activities and investments. They won’t. If oil companies were concerned about tomorrow they would be setting up R&D efforts to manufacture fuels using nuclear power. If our government was concerned about tomorrow they would require these R&D efforts. They aren’t interested nor are they concerned about tomorrow. And this is because we have taught to rely heavily on the short range outlook present value of money. Even if we programmed in extinction in 100 years into our economic model the PV analysis would not be concerned today.
So now tell me that 100% reliance on an economic model that will eventually lead to my death at some point in the future wise idea. We are sailing in a fog using just the PV economic model alone. We need to turn on the radar and take a longer range view of where we are headed.
Gene,
It appears that you have decided to take a contrarian point of view.
Inflation is only measurable in hindsight. There is no alternative.
Future inflation is able to be guessed at, and that I have covered already. If you are not prepared to accept that, then so be it. However, you appear to place your own gloomy prognostications above the knowledge and language of finance and economics. We are, thus, talking in different languages.
1. I have already discussed concisely how expectations of different future inflation scenarios can be modelled and why this is beyond the realm of LCOE. Financial modelling is not a matter of bashing opinions against each other, it is mathematical. If you don’t wish to base your future expectations on modelling, then we are only discussing opinions, which leads to unsolveable problems. Who can shout loudest and longest? That is no way to make decisions.
2.
There was no first mistake. Similarly, I have not said or meant to imply that “corporations will save us”. That is simply silly. What I have tried to do is to explain how corporations handle financial risks, especially those relating to expectations of future inflation of input prices.
I have offered examples from my own experience and have discussed the limitations of LCOE calculations, which are primarily tools used for comparisons of energy options, versus the more detailed financial modelling which is essential before committing billions of dollars to any venture, whether energy related or otherwise.
It is nothing more than an insult to attempt to brush this aside with unresponsive and uncomprehending opinion.
The fog of which you speak is not the result of economic or financial modelling and cannot be lifted by chanting slogans. It may be partially lifted through analysis and technology and teamwork. Ignorance is not radar. So-called longer range views of the type “In the long run, we are all dead” are neither insightful nor helpful, even if coming from folk who are on our own team.
This thread contains some excellent comments and some nonsense. It has been getting away from being constructive, IMO.
I decided to sit back and watch for a while. I suggest, if getting nuclear in Australia is as important as most BNC contributors think it is, then it would be most constructive to focus on what is imiportant.
The following is unhelpful IMO:
– Avoiding discussing and trying to identify the cost drivers that are making nuclear too expensive (based on LCOE analysis done specifically for Australia by an authoritative source)
– Arguing about the validity of the LCOE method for use at this stage
– Discussing ideological positions such as “discount rate is not valid” (and the evils of capitalism, money, debt, equity and interest).
– Comments about the invalididty of the analysis when the commenter had not read the paper carefully “These studies are meaningless because CCS fails a simple legal test.”
Can we at least accept that capitalism is here to stay; we are not going to change that. Discount rate is the way we value long term investments; we are not going to change that. LCOE is a valuable and useful tool for doing the sorts of comparions done by EPRI and for the sort of analysis presented in the lead article. If the LCOE method isn’t valid, why would IEA, EIA, OECD, RAE, MIT, NREL, NEEDS, Treasury and virtually all the authoritative organisations that do these sorts of comparisons use LCOE?
Can I urge us to get back to:
– pointing out any important and relevant flaws in the analysis and the EPRI study. Please indicate the size of the error and how it shold be corrected
– accept the analysis and the results are OK and move on to the next step: what would need to be done to allow nuclear to be economically viable in Australia (and I’d argue there should be the caveat “without damaging our economy”).
Peter Lang — Fine with me!
It might be that the validity of the EPRI figures, generally, can be assessed by projects which tehy rated and also have been constructed in Australia. For example, if EPRI assessed wind farms it seems there are several which have been completed in various parts of Australia.
This might be relevant as (if I recall correctly) wind farms in Australia are much more expensive than here in the Pacific Northwest. To establish the goal, right now wind energy contracted wholesale price to Idaho Power has an LCOE of US$0.083/kWh.
Peter Lang,
accept the analysis and the results are OK and move on to the next step: what would need to be done to allow nuclear to be economically viable in Australia
Compared to what?
It would be hard to make a purely economic case for nuclear anywhere in the world compared to coal at $1.50/GJ. Most of the world doesn’t have $1.50/GJ coal.
harrywr2,
So?
Nuclear fuel is about half the price, $0.78/GJ 🙂
harrywr2, @ 10 November 2011 at 3:59 PM
Thank you for your comment.
Not compared to anything. Just simply, are there any errors in the analysis? Are the abatement costs correct, given the inputs? Is there any significant error in the inputs? That is the first step.
I’ve concluded from the discussion so far that no serious errors have been identified, so far. But many readers do not like the figures so the discussion gets diverted to other arguments such as the validity of the concept of discount rates and the LCOE analysis method. IMO, those discussions are a distraction.
In that case, Australia should be one of the last countries to move off coal. Until there is an international agreement on how to cut GHG emissions, we would be shooting ourselves in the foot by implementing policies to force expensive electricity for no benefit to the world (no reduction in global emissions) and serious consequences for Australia’s economy (i.e., for people’s well being). It would make us less able to implement the appropriate policies, including adaption policies. This is obvious. For substantiation for these statements see: http://bravenewclimate.com/2011/07/06/carbon-tax-australia-2011/#comment-136435 and subsequent comments.
If we want low cost nuclear, we need to be prepared to let go of some of the impediments that are constraining us. If Korea can have nuclear for $2,500/kW and China for even less, then why can’t we have it for close to those figures? We need to be prepared to approach this with an open mind, IMO.
What is lacking in the analysis is the cost of a 7 meter ocean rise in about 100 years. This possibility is now in the minds of some of our best thinkers because they can project what is currently happening into the future. The present value of the future 100 years discounted at 10% annually is (future$)*1.1^-100 = (Future$)(.00007). So even if we did plug in trillions of dollars as the future cost of dealing with a 7 m ocean rise, it still has no present value impact in today’s decisions. This is the shortcoming of present value analysis. Its equivalent to harvesting a forest and not replanting it for the next generation.
For sure a 7 m ocean rise 100 years in the future will have a lot of meaning to those people 100 years from now, our kids. From their persective the CO2 problem would have been much easier to solve at our present time than in their future time. So they will see us as choosing to enhance our economic wealth at the expense of theirs.
Choosing to ignore this future problem might mean the person doesn’t believe there will be a 7 m ocean rise even though there is good evidence, or possibly they just don’t care. I’m afraid this is turning into an evolutionary test for humans. Are we up to the challenge?
Indications from this article suggest that an overall large monetary cost to completely replace any electricity generating technology is a given, regardless of whether it’s to mitigate CO2 emissions or not
France Can’t Afford to Give Up Nukes, Utility Chief Says
In particular, this struck me:
(emphasis mine)
The major difference here (i.e. going from nukes to coal instead of the other way around) is that there are no savings from greatly reduced external costs, which are paid for by the public (health, pollution, contribution to global warming, etc.).
I recollected a couple of other EPRI documents I’d encountered (regarding the elasticity of demand) . They changed significantly within only two years.
So I looked back, and found in 2005 EPRI produced a document, Nuclear Energy in a Carbon-Constrained World, which seems to put nuclear costs at about $60/MWh. That document also puts a ‘value’ on nuclear energy in different carbon constraint scenarios.
The recent EPRI document notes that ” (LCOE) for each technology was estimated based on a simplified version of the Revenue Requirement Methodology. The simplified COE methodology utilised a spreadsheet approach to ensure transparency of the results. Financial parameters, including assumed capacity factors, were reviewed by the AdvisoryGroup…”
I noted shortcomings of the model previously, and P.L’s spreadsheet anticipated the criticism. Choosing wind would have to trigger also choosing a second supply, which would in turn mean the capacity factor of the second source chosen would drop. A proper model is difficult to put in a spreadsheet.
The model also assumes costs will drop rather significantly for CCS. I am not convinced that is known – or knowable. I see no reason the EPRI model is reliable in estimating the actual cost of “CO2 abatement” – and my earlier comments should have stated I think a more complex model would show nuclear and CCGT, alone in the mix, would be the lowest replacement cost method of CO2 abatement – a conclusion not dissimilar to KPMG’s fresh reporting on the UK . http://www.kpmg.com/UK/en/IssuesAndInsights/ArticlesPublications/Documents/PDF/Market%20Sector/Power_and_Utilities/new-nuclear-an-economic-perspective.pdf
I didn’t say that, and we ended up discussing the LCOE for generation, This is clearly tied to estimates on the cost of capital, and I think Peter Lang’s “Can we at least accept that capitalism is here to stay” statement probably defines discussing the details on that. A free market without a cost on externalities/emissions should do what it is doing.
Australia has the comparative advantage of abundant coal. If Australia spends on nuclear, chances are more coal is exported elsewhere – so all that occurs is more fuel is used in shipping. The economics dictate Australia generate it’s electricity with it’s coal.
I’ve opined before that the economics seem to indicate the elasticity of replacement for energy are greater than the elasticity of demand – theoretically just banning coal would bring alternatives to market quicker, and cheaper, than models, such as EPRI’s produce. Australia would then lose all the value of the coal in the ground. In a CO2 abatement world, the scenario where Australia retains that ‘wealth’ is CCS. The EPRI study justifies that course of action – perhaps by design.
But, if the financing was provided by a government, at cost, the figures would be drastically different. The EPRI study shows debt as 70% of all financing, at a cost of 9% with a 6.3% return. Eliminate the return and things change rather quickly. You might consider doing that for the same reason the Hoover and Grand Coulee dams were built. There are times when governments just want to get money circulating.
The valuation choice ends up between mitigating climate change, and the value of coal extraction. Again, economically, the outcome of that choice is known. The monetary benefit is immediate, while the costs of climate change are not.
Immediate wins.
harrywr2, on 10 November 2011 at 10:21 AM said:
This comment reinforces these points:
1. Nuclear cannot be viable in Australia at the currently expected costs.
2. CCGT, not nuclear, is the least cost way to reduce emissions in Australia, at least until much of the coal fired power stations have been replaced.
3. A carbon price of $107/tonne CO2 would be required to make nuclear a viable option (in the absence of other market interventions, incentives or disincentives to favour nuclear).
4. This means Australia would have to pay a higher CO2 price than probably any other country.
5. Such a high price for CO2 has not been justified (by impartial, authoritative sources).
6. Australia should not lead the world with the highest CO2 price penalty. (Deleted personal political inference)
7. CO2 pricing is not going to remove the impediments to low cost nuclear. It won’t even force us to look at what needs to be done to remove them. Instead, the easy way will be to continually lift the CO2 price until nuclear is viable with the impediments remaining in place. CO2 pricing will cover up the issue, as has been so amply demonstrated by two years of BNC contributor’s avoidance of the issue of how to remove the impediments to low-cost nuclear (see the comments on this thread: http://bravenewclimate.com/2010/01/31/alternative-to-cprs/ )
Scott Luft,
Excellent comments. Thank you. Some really clear, deep thinking in this. I’ll think for a while before responding.
Some inputs for LCOE analysis used in the ALSTOM paper (June 2011): “Cost assessment of fossil power plants equipped with CCS under typical scenarios.”
Peter Lang, it was I who directed the moderator to make those edits. As I’ve said to you before, if the moderation policy as applied on BNC grates too much, then you have options elsewhere on the internet. It is fair in the sense that I believe it is fair, and that is all that counts here. So as galling as it may be to you sometimes, please grit your teeth and accept them as being done for the good of the blog, and in the interests of getting and keeping the most people onside to your way of thinking as is possible. Perhaps it will help if you think of the moderation policy as akin to a purse-lipped teacher who strides about a class of intelligent but sometimes belligerent schoolboys, brandishing a ruler and occasionally whacking it over the knuckles of those who get too rowdy, stir others too much, or don’t follow the class rules.
In sum, I must ask you to no longer complain here in the comments about moderation (do this via private email if you feel the need to vent). Otherwise, I’ll be forced to leave you on comment-by-comment moderation to avoid having these slip through, and neither of us want that.
Peter I will agree the EPRI study and LCOE makes good economic sense if the analysis is performed in a conventional sense. I have done a jazillion studies exactly as you would expect, looking a cash flows and minimizing the total present value expense or alternatively maximizing profit.
However there is a new problem lurking in the distance. Take a look at this NASA site showing a rise in the CO2 level.
http://www.noaanews.noaa.gov/stories2011/20111109_greenhousegasindex.html
The rise was 29% from 1990 to 2010. The so called 400 ppm tipping point is at hand in about 4 years (I think). How high do you think the CO2 level will go before Australians will begin to take the CO2 rise seriously – i.e. in the economics and decision making. I had not seen this mentioned in your analysis so I think you are probably purposefully avoiding the issue.
Gene Preston,
Thank you for your comment.
You are quite right, I have not mentined it in this analsys. I specifically excluded it in the Introduction, which says.
There are hundreds or thousands of analyses that do address the effects of CO2, externalities, CO2 pricing, etc. This paper has taken a different tack using the LCOE figures that the government departments are using for their analyses and decision making. I believe this approach is valid. This is a foundation stone for what follows. If there are errors in this analysis we need to know. So could you please focus on this analysis and its purpose, rather than try to go of in different directions (yet).
The purpose of this analysis is to show what the CO2 price would have to be to make the various technology options viable. For nuclear, the CO2 price would have to be $107/tonne CO2 (in the absence of other incentives and disincentives and given the current investment climate in Australia). This is based on the EPRI figures. In fact, the nuclear case may be worse than stated, because investor risk premium is not included in the EPRI figures. IMO there is no way that CO2 price can be raised that high, and nor should it be. Therefore, we need to look at other ways that will be acceptable.
If you want to see what I’ve been writing on CO2 tax and ETS, then I’d refer you to the CO2 Tax thread from here http://bravenewclimate.com/2011/07/06/carbon-tax-australia-2011/#comment-136435 to the end of the thread. That will give you a pretty good understanding of where I stand.
The “lead article of the “Alternative to Carbon Pricing” thread also gives a good idea of how I suggest we implement nuclear in Australia.
Now I hope we can get back to discussing the lead article on this thread.
My estimate is that 107 $/metric tonne for CCS translates into 14.6 cents per kWh using a 1000 MW coal plant producing 3 million lbs CO2 each hour. This seems a bit high, maybe by a factor of two. In the US coal is a little cheaper than nuclear, but if you add CCS, it doubles the cost of energy from coal, making nuclear by far a cheaper alternative.
You had said “Based on EPRI’s estimates, nuclear is not economically viable in Australia because it is too expensive. This situation will remain while the impediments to low-cost nuclear remain in place.”
What are the impediments in Australia stopping nuclear power? In the US its a deregulated market that is stopping nuclear, not because of the energy cost, but because under our deregulated no one can afford to build anything because the risk to a capital investment is too high in a deregulated market. So in our deregulated environment, not even gas plants can be built at a low investment risk. And that is why rolling blackouts are going to be the norm soon here in Texas.
Build Time Differences
Since interest costs during construction can be in the area of 30% of the cost to build a nuclear plant, it is important to estimate the construction time correctly. Construction time is defined here as from first concrete to fuel load.
I have been comparing the Australian and the English levelised cost studies.
England study link – http://www.decc.gov.uk/assets/decc/11/meeting-energy-demand/nuclear/2153-electricity-generation-cost-model-2011.pdf
It is strange that the two studies come to opposite conclusions. The English study shows nuclear to be the cheapest option.
From appendix D of the English study – Areva says construction is likely to take 42 months, i.e. 6 months longer than Westinghouse. The figures show this 6 months difference.
From section 6 of the Australian study – The first US contract agreement since Three Mile Island was signed in April 2008 by Georgia Power Company for two AP1000 reactors. It is estimated that the construction period will last approximately 36 months.
It appears that both studies seriously under estimate the construction time by taking the company estimate. Also, it appears that the time of construction is same for the first of a kind in a country and the Nth of a kind in a country.
The AP1000 builds in China appear to be on schedule but the schedule is 50 months from first concrete to fuel load. At the Sanmin site first concrete was 3/09 and fuel load is scheduled for 5/13. The AP1000 build in the US plant Vogtle may start 1/12 with a finish in 2016. About 50 months also.
Both the Areva EPR in Finland and France are years behind schedule. However, the Chinese EPR seem to be on schedule and plan to take 44 months. The Taishan start was 10/9 and the projected finish is 12/13. (If I can remember, I will look to see how the AP1000 and the EPR are doing in December of 2013.)
It would seem reasonable to use 50 months for the first-of-a-kind-in-a-country and decrease to 36 months for Nth of a kind.
I assume that adding 14 months to the construction time increases the cost quit a bit.
@Martin Burkle,
It appears that both studies seriously under estimate the construction time by taking the company estimate. Also, it appears that the time of construction is same for the first of a kind in a country and the Nth of a kind in a country.
There are build time estimates with/without contingencies.
The VC Summer Schedule(pdf page 26)
http://www.scana.com/NR/rdonlyres/A830A131-9425-46F1-B948-C8424530EE49/0/2011Q2BLRAReport.pdf
shows an 18 month contingency. If you scan down to item # 60 – there has been a slippage of 12 months in the coolant loop pipe fabrication. But item #130 – Hot functional test has only slipped one month and item#133 – Unit 2 substantial completion hasn’t slipped at all. It’s also interesting that ‘first nuclear concrete’ is item #69 on the project plan. It would appear that in the AP1000 build plan substantial verification of ‘long lead time’ items is made prior to pouring concrete.
One would ‘think’ that at nth build supply chain issues would be resolved. Of course if one is ‘maximizing local content’ then the supply chain problems could repeat.
Gene Preston, @ 12 November 2011 at 9:31 PM:
From this and most of your comments on this thread it seems you have not read the lead article carefully. Could I urge you to, please, read it carefully and understand the whole article as a package. Then hopefully, if you find something wrong in the article – as opposed to hand waving – you can point to specific errors.
Excellent question Gene. I’ve been urging BNCers to focus on getting to the bottom of what thye are for the past two years. It is not a subject anyone on BNC has shown any inclination to go near. It would involve questioning some deeply held ideological beliefs. I have posted many comments on just the question you ask about on the “Alternative to Carbon Pricing” thread (which is accessible by clicking on the “Renewable Limits” tab [click on the tab don’t hover over the contents list that comes up when you hover over the tab]).
Furthermore, Also please refer to this comment on this thread:
@ 5 November 2011 at 8:52 AM
I can provide you with a list of links to some previous comments that paretly address your question. However, my main point for the past two years is that we need to identify the impediments to low cost nuclear in Australia before we can work out which we could remove and how we could best go about it.
Martin Burkle, 13 November 2011 at 4:27 AM
These are excellent points. They get to the heart of one of the most important uncertainties in LCOE estimates.
EPRI provides a short description of five of the main Gen III technologies available at the moment, including the vendor’s claimed construction duration. For AP1000 they quote 36 months construction duration. Furthermore, EPRI has used a 1,117 MW plan for its baseline nuclear plant, so we can conclude their LCOE analyses are based on the AP1000.
However, EPRI does not specifically state what construction period they have used for their LCOE analysis. I suspect they may have used a long duration as the basis of their LCOE figures. The reason I say this is because the capital cost figure ($/kW) we need to enter in the NREL LCOE calculator to give the capital component of LCOE, $114/MWh (see EPRI, Table 10-13 and convert to 2011 US$), is $9,207/kW. This is much higher than other figures quoted elsewhere. This is comprised of $4,763/kW for Total Plant Cost (EPRI Table 9-2 converted to 2011 US$) plus (by subtraction) $4,444 Owner’s Costs and AFUDC.
The EPRI report does not state what is included in the $4,444 of what I am assuming comprises Owner’s costs plus AFUDC. The EPRI report states they have assumed Owner’s Costs amount to 15% of Total Plant Cost. But Owner’s Costs plus AFUDC amount to 93% of Total Plant Cost. This suggests a large AFUDC component and therefore, a long construction duration.
How EPRI has calculated the capital cost component of LCOE is a mystery (to me).
I should point out that the ACIL-Tasman report gives a more detailed description of their LCOE calculation. The Owner’s Costs are not included (from memory) and the AFUDC is calculated in the program from inputs about assumed cash flow during the construction period (through to the start of commercial operation). The EPRI and ACIL-Tasman calculations also differ in that EPRI is done on a ‘before tax’ basis and ACIL-Tasman on an ‘after tax’ basis. The ACIL Tasman report exposes that there is a considerable tax penalty for nuclear compared with coal. That is just one of many of the impediments to nuclear we need to address.
Harrywr2,
Excellent points. However, as you would know (but I’ll spell it out for those who do not), delays of individual milestones do not say how much the project completion date will slip unless we also state that the milestones is on the critical path. The milestone list does not say which milestones are on the critical path, nor how much float (slack to Americans) is on each milestone.
For readers not familiar with these terms (critical path, float and slack) see definitions here:
http://en.wikipedia.org/wiki/Float_(project_management)
@Peter Lang,
Yes, without knowing how much float/slack is in each milestone we don’t know what the impact will be or the build time on NOAK units.
Just as background history…Vogtle #3 and #4 in Georgia, the US FOAK for the AP1000 is just a couple of months ahead of VC Summer #2 and #3 in South Carolina. Georgia and South Carolina are neighbors.
The history on Vogtle #1 and #2 was they were originally budgeted at $660 million and ended up costing $8.8 billion(1980′s dollars). So there is some ‘sensitivity’ in the region about the words ‘delay’ and ‘cost overrun’.
Given the ‘sensitivity’ I would be very surprised if there isn’t a lot of float in the project plan.
Harrwyr2,
Thank you for that. All this information helps us to work out what we will need to do if we want to remove the impediments to low-cost nuclear in Australia. The first step is to identify what all the impediments are, quantify the effects on LCOE, prioritise them in terms of: the effect on LCOE, consequences of removing them (effect on other systems), ease of removal, and time line for removing them.
harrywr2, on 13 November 2011 at 5:35 AM said
This raises an important, and often contentious, point. Should we or should we not impose constraints on the contractor that forces the contractor to meet a specified proportion of Australian Industry Involvement?
If we do, the cost of the plant will be higher. If we don’t we may not develop expertise in Australia in nuclear technologies as quickly.
We have a parallel in defence procurements. Australia is considering whether we should build our next fleet of submarines ourselves or buy them overseas. The cost difference is likely to be more than a factor of two and there will be a lot of problems if we build them ourselves. But there are considerations about the flow on effects of keeping industry in Australia as well as Australian independence in submarine warfare. Similar debates will no doubt apply to implementing nuclear power in Australia. From my perspective, we need nuclear to be least cost so it will be rolled out faster and so Australia can assist developing countries to choose nuclear over fossil fuels. I believe we will learn fastest by just getting on with it. To do this means adopting the least cost approach whatever that might be.
Adopting the least cost approach may mean, for example, allowing the vendors people, e.g. Koreans to enter Australia to build and operate the plant for an extended time, without requiring that they be employed under Australian industrial regulations. (Personal political inference deleted)If we want least cost nuclear, for all the benefits it would bring, then I’d suggest we need to open our minds to all options.
Martin Burkle or anyone,
Further to my 13 November 2011 at 9:23 AM response to you, and your comment:
I am still struggling to understand why EPRI has what I am interpreting (perhaps incorrectly) to be an Owner’s Cost plus AFUDC of 93%.
AFUDC for VC Summers 2 and 3 [1] is $249 million out of a total plant cost of $5,371 million, or about 5%. EPRI states that it allows 15% for Owner’s costs (as do OECD 2010 and IEA 2011). Those total about 20%. How does EPRI get 93%? What am I missing?
[1] http://www.scana.com/NR/rdonlyres/A830A131-9425-46F1-B948-C8424530EE49/0/2011Q2BLRAReport.pdf , Appendix 3.
EPRI Construction Cost Mystery
“How EPRI has calculated the capital cost component of LCOE is a mystery (to me).”
Peter, I am confused. Please tell me what I am missing.
Your article basically says, “Assume that the EPRI report is correct. Since nuclear is too expensive for Australia, what needs to be done to make nuclear competitive in Australia?”.
Now after 170 comments you admit that even you, an expert, can not figure out the capital cost component of LCOE in this report. We all agree that the capital cost component of nuclear is VERY important (and we all don’t agree on much).
So, Peter, why would you ask me to assume that the EPRI report is correct when you can’t figure out where the large cost of nuclear comes from?
The EPRI cost for nuclear appears to be too high but appendix 1 says a build time of 36 months is expected for an AP1000. This build time is too short especially for the first Australian build. So the EPRI construction cost should be higher still.
Conclusion: Australian nuclear build costs may be too expensive or not. The EPRI report can not be trusted because it is not detailed enough to know nuclear construction costs.
It is my understanding that finance for nuclear plants in the US often comes at a premium because of the risk of political interference during and following construction (Shoreham is the classic example of how badly things can go wrong with this). Did the EPRI estimates take this into account? If so, there’s a pretty obvious way to attack the problem.
Martin Burkle,
I pointed out in the paper that the EPRI report is “obscure in parts”, doesn’t explain all the input s needed for calculating the capital component of LCOE and that Total Capital Required is 1.93 times Total Plant Cost.
I do not understand how the capital component of LCOE is calculated in the EPRI report. I cannot get the capital component of LCOE for the ACIL- Tasman report to match their stated values. Both reports do not specify all the cash flow and other inputs you’d need to calculate the LCOE they way they have done.
When I say I don’t understand their method, I am not saying that I dispute their figures. I put the discrepancy down to me not having the knowledge or tools to be able to replicate their outputs.
I strongly suspect their figures are correct, and probably realistic for Australia. There is a remote possibility they are wrong. I am urging that we accept their figures and move forward because I see no other realistic option that will allow us to move forward. The reason I say that is because we cannot expect to be able to get Treasury and the many other organisations to re-do their carbon tax and ETS modelling. Furthermore, AEMO contracted Worley Parsons to check the EPRI figures and conduct sensitivity analyses on the effect of varying the input parameters. So I believe the EPRI report will have been given very close scrutiny by Worley Parsons, AEMO, Treasury, ABARE, ACIL-Tasman, all the big financial firms, ESAA, the electricity generators, BZE, and many others who have the competence to do so. Thirdly, LCOE analysis is standard practice for EPRI. It is unlikely they would get this wrong, and if they had an error it would probably have been found and corrected by now.
Therefore, the “highly likely” situation is that EPRI figures are correct. If there was an error, it is “highly likely” it would have been picked up by now.
Hi Finrod,
Investor risk premum is not included in the EPRI analyses. The analyses use the same discount rate for all technologies: 8.4% real before tax.
Investor risk premium would need to be added to this discount rate. I agree investor risk premium is one of the major impediments to nuclear in Australia and it is one of the most critical issues we will need to address (and remove) if we want nuclear.
MIT (2009) [1] estimated the investor risk premium for nuclear in USA is 26% (from memory). I expect it would be much higher in Australia.
You have hit on one of the most significant hurdles we need to deal with (IMO).
[1] MIT (2009) “The future of nuclear power”, 2009 update.
http://web.mit.edu/nuclearpower/
Several commenters have suggested or implied that we should return to an earlier time and reintroduce state ownership or increased regulation to make nuclear viable. This is Keith Orchison’s take on this (released this afternoon) http://www.businessspectator.com.au/bs.nsf/Article/NSW-power-privatisation-OFarrell-unions-profit-deb-pd20111114-NKV87?OpenDocument&src=pmm .
The point of my previous post (extracts from Keith Orchison’s article), is to say that we should not waste our time arguing about whether Australia should reintroduce state ownership or stronger regulation as a way to implement our preferred solutions. That is simply not going to happen. Australia is heading towards transferring the electricity generation assets to private sector so it can free up the value to invest in what only the public sector can do. We’ve been heading in this direction for over twenty years (as have most other western democracies) so to suggest we will turn back is unrealistic.
Martin Burkle, 14 November 2011 at 11:20 AM
I can’t see where the EPRI report states it has used a 36 month construction period as the basis of its LCOE estimates. I said this in an earlier comment. I cannot see any mention of 36 months in the EPRI appendix nor in the appendices to the lead article for this thread. So I am confused as to what you are referring to. I am now wondering if you read all of my comment @ 13 November 2011 at 9:23 AM, which included this:
Scott Luft, @ 11 November 2011 at 12:59 AM:
I said I’d return to this thought provoking comment.
I’ve read it again, carefully. I agree with all you say until the last paragraph. I have some issues with some of the statments in the last paragraph, but they are minor; I think the comment is interesting and important. I would urge interested readers to re-read it.
I am not sure what you mean by “at cost”. I’ll assume you mean at the rate the government can borrow. But doing this has costs for society. The money the government borrows for electricity generation cannot be used on other capital investment projects that only the government can build, such as hospitals, public transport and investments for environmental remediation. If the government borrows too much money it squeezes out the private sector. If we go too far, we end up in the mess Europe is in. So, I am far from convinced that public ownership of electricity generation is the right approach.
The assumed interest rate on debt is 9% (Current) or 6.3% (Constant). Debt comprises 70% of the funding, so the debt component is 9% * 70% = 6.3% (Current) or 4.4% (Constant). EPRI’s report works in Constant dollars throughout. At first I didn’t understand what you meant so I’ve laid it out so others can follow.
We cannot do that. That would put private sector generators out of business. They’d go broke. When we have a mix of private and public sector generators, as we have in Australia, the public sector has to pay a dividend to the government at the same rate as the private sector to allow the private sector to compete. See the full Keith Orchison article (link in previous comment) for some up to date figures on the dividend the NSW generators have to pay to the NSW government.
That might be the correct approach in a depression, but not now, especially since the EU and USA are up to their eyes in debt. Instead, we should remove the mass of regulation that is strangling innovation and business and forcing manufacturing to move to Asia.
I have some concerns about bits of this, but can’t address that here. I believe we can cut global emissions without damaging the economy.
Peter is the EPRI LCOE of nuclear capital cost higher or lower than you would expect? I thought LCOE could only be calculated one way.
David, we need storage when wind and solar become so large that their power swings are not manageable by ramping convention generation. ERCOT is there right now and with wind expected to double in next few years the ERCOT engineerf are doubting they can make the system operate reliably. The near instant power swings are getting close to exceeding the loss of a large nuclear plant and our spinning resereve is set to cover that loss. Larger than that causes the frequency to drop and automatic load shedding.
Possibly the EPRI financing interest is higher than the LCOE discount rate. Like I had said it depends a whole lot which utility is building the nuclear plant as to what the financing interest is. It was 11% for ERCOT because of our screwed up market design but could be 5% for Southern Company if they showed the sales of the nuclear plant energy was for certain and the collection of revenue from sales was secure. The reason nuclear looks so bad in the US is nearly entirely due to regulatory or deregulation reasons, not technical.
Peter the movement to privitization and/or the deregulation of AU’s electric system is a big mistake. Its been a disaster for us here in Texas. The publically owned utilities offer much lower rates and are doing a much better job of planning their future systems. I am just waiting for this deregulated system to have rolling blackouts and the citizens are going to get so mad then the whole system will be redesigned from the ground up. Keep an eye on this development.
Peter you said:
“We cannot do that. That would put private sector generators out of business. They’d go broke. When we have a mix of private and public sector generators, as we have in Australia, the public sector has to pay a dividend to the government at the same rate as the private sector to allow the private sector to compete. See the full Keith Orchison article (link in previous comment) for some up to date figures on the dividend the NSW generators have to pay to the NSW government.”
This is insane. This means that the public pays a subsidy to the profiteers? I build a power plant and because the private companies do not like me generating my own power, they bill me? This isn’t competition, its highway robbery. Its the poor subsidizing the rich. This is no way to keep the lights on. The only reason you might have low rates is because you have cheap coal. What does Australia do to keep rates reasonable? Otherwise the profiteers would just keep rasiing rates and raising rates.
Peter, you gota get the detail.
Thank you for explaining your position as “EPRI is the best information we have. Let’s use it as a starting point to see what policies and practices could reduce the cost of nuclear”.
This is a reasonable business position. It is normal to take a troubling business report and drill down to the detail level where business practices can be changed for the better. It is also normal that the required detail is not in the original report. Managers will have follow up meetings that often become both very detailed and very nerve wracking for the report writer (OMG did I get this report right?).
Now, we have a troubling EPRI report. We would like to drill down to more detail so we can think about Australian policies and practices that would reduce the cost of nuclear. But it seems to be impossible to get more information from EPRI. In the US there is a freedom of information act that is sometimes used to extract more information from the government. I picture Australia as a smaller community where such formality is not required. Can’t you just ask one of the authors for more detail?
I assume the answer is “No, we can not get more EPRI detail. The detail is a closely held secret guarded by privilege and lawyers”. If this is the case then I really wonder about the motive of the “protectors of the detail”.
It is not logical to guess at reasons why the EPRI nuclear cost is so high and then act on those reasons. The detail not only contains the reasons but the extent of each factor. Let’s use my example, I think that the construction duration used by EPRI is 36 months because 36 months is used in the appendix for the construction duration for an AP1000. Peter, you infer a longer construction duration was used because you don’t see how the cost could be so high using 36 months as the construction duration. We need to know whether they used 36, 48, or even more months. If the construction duration could be reduced from X (EPRI report months) to 36 months, then we would know how important construction duration is to nuclear cost.
We disagree after reading the same report. Back when I worked for a living, it was not at all unusual for me to read a design and disagree with someone else who read the same design. The managers would grimace and call a meeting including the disagreers and the writers of the design. Sometimes it was a misunderstanding on my part. Sometimes the the design needed to be improved.
The EPRI report was to inform public policy decisions. The EPRI detail could be used to inform public policy. In order for the EPRI report to be the “best information we have”, you have to get the detail level information.,
Gene Preston, @ 14 November 2011 at 9:32 PM
Thank you for your question and comment.
As I’ve explained several times on this thread, the EPRI LCOE figures are the best we have to work with at the moment. They are authoritative because they have been prepared by a groups who is expert in the field and because have been checked by numerous groups and widely adopted by the key government departments including Treasury, ABARE, Deparrtment of Resources, Energy and Tourism, and AEMO to name a few. So to try to develop our own figures and get anyone to take any notice would be futile.
Furthermore, I suspect the figures are realistic for Australia given the masses of impediments to nuclear power we have in Australia.
No. There are many ways to calculate LCOE. Here are a few:
Constant or Current $
Before or after tax
Many other financial and economic assumptions included or excluded
What is included in ‘Capital’ or handled elsewhere in the computation algorithims
Simplified NREL calculator or more sophisticated expressions
Refer to Section 2 here http://www.aemo.com.au/planning/419-0035.pdf for a lot more about LCOE calculations.
Gene Preston, @ 14 November 2011 at 9:39 PM
I’ve answered all tha t previously on this thread. Could you please go through the article and read the responses to comments.
Like I said, the EPRI study is not a site specific or market specific analysis. It is not a financial analysis (I’ve already said all this in earlier comments on this thread; are you reading them?). It is a comparison of technologies using the same discount rate for all technologies. If we add in investor risk premium and remove incentives and disincentives, renewables could not be built at virtually any discount rate and the nuclear would have a high investor risk premium. So the true LCOE of nuclear in Australia would be far higher than the EPRI figures without major government incentives.
Gene Preston, @ 14 November 2011 at 9:50 PM:
I know you believe that, and so do some other engineers who have spent most of the early parts of their careers in the government owned electricity industry. There certainly are advantages and disadvantages of public ownership / strong regulation.
However, most people believe that the private sector can run it better.
Importantly, there is no turning back. It’s reality is it is not going to happen. The whole momentum is to sell off the remainder of the government owned assets. To try to argue against this is a waste of time.
Governments can no longer afford to provide the capital the electricity industry needs. Government’s have urgent needs for whatwver capital thay can raise. Thise needs include: health system, education, public transport, roads, dams and defence. We’ve been steadily increasing the total tax take and spending it on social welfare programs. We can no longer pay for electricity, telephone, banks, groceries etc to be provided by the public sector.
Get over it, Gene. It ain’t going to happen 🙂
Gene, @ 14 November 2011 at 10:20 PM
That is left wing ideological silliness, IMHO. It is the same sort of nonsense that gave us mandated renewable energy and CO2 tax and ETS.
If you want electricity to be run by the state, do you also argue that telephone, internet, television, media, banks, groceries, petrol, gas should be run by the state? If not, why not? (By the way you are in good company because many in the Labor and Greens in Australia would agree with you).
Did you see this when I posted it a year or so ago?
Malcolm Grimston (June 2010), Chatham House Electricity – social service or market commodity? The importance of clarity for decision making on nuclear build.
http://www.chathamhouse.org/publications/papers/view/109378
I differ from the greens in several ways. I do not believe in government subsidies. I do not believe the wind and solar are good investments because they return too little energy for the invested dollar. The open market competition model does not work either because it cannot see more than a few years into the futue. We need a new economic model unlike what we have ever had in the past and completely different from what we have now. You know what I believe. I believe that the long range energy supply can only be financed efficiently through the energy annuity concept: see http://thesciencecouncil.com/eugene-preston/196-a-new-way-to-finance-high-capital-cost-projects-using-and-energy-annuity.html
There is no other model that solves the financing problem for nuclear and even for solar, for those individuals who want to throw their money away. But that should be their choice, and we should not be subsidizing these energy sources. What governments should be doing is funding R&D on new processes and thats it.
Martin Burkle, @ 15 November 2011 at 2:26 AM:
Martin, this is an excellent comment, all the way through. Thank you. I hope many people will read it and read it a second time.
You’re right, of course.
I’ve been thinking for a while I should try to contact someone in the Department to see if I can get some of the detail as you suggest. If I can’t I’ll write to the Minister.
I wasn’t sure how, or if, to respond to your comments on my previous post – without going off on some tangents.
My point on coal was for Australia to meaningfully, and affordably, move off coal is for the world to have a better option. Wealth is what has value – and that includes, currently, the coal in the ground. I mention it as a hurdle that needs to be overcome.
We want to devalue coal, don’t we?
Secondly, I didn’t discuss public power at all, but I see the concern. Offering a financing advantage to one source would be like offering priority purchases at guaranteed high rates for long periods of time. Like the feed-in tariff, and renewable energy standard programs do…
Or allowing externalities, like emissions, to be unaccounted for…
Well, I also see my point. Picking where to distort a market also picks technologies. If you have a market for providers of electricity on 30-year power purchase agreements where the state lends at their cost of borrowing, you still have a market.
You just have a market for nuclear.
Scott Luft, @ 15 November 2011 at 12:30 PM
Thank you for another thought provoking comment.
Yes, coal is an asset as long as it is valuable (e.g. for generating electricity, making other fuels and making steel).
OK. But why pick on just one externality? Why pick on CO2? Why not pick on any number of other far more important externalities?
And what about the external benefits of low cost electricity generation. How do you account for those?
A better way to make the transition to low emissions electricity generation, IMO, is to allow nuclear to compete with coal for electricity generation. Fifty years of misguided policies and regulation have made nuclear higher cost than it should be. These have made it uncompetitive in the developed world and less competitive than it should be everywhere. This is slowing the progression from fossil fuels to low emissions electricity generation. Instead of further distorting the market with more regulations and misguided bureaucratic interference, I’d urge we take direct action to remove the impediments to nuclear.
Scott,
could you please expand on the point in your last paragraph
Is this a truly level playing field for all generators, for all energy sources, for all other industries that would want to borrow money at government rates? Why should electricity get special treatment over other critically important public infrastructure such as dams, public transport, health system, etc?
The capital cost for nuclear (central estimate, Real 2009-10 A$/kW) = A$5,283 in 2015 translates to US$4515/kW which is in good agreement with VC Summer capital cost.
DBB,
Yes,, but remember that is the Total Plant Cost not the Total Capital Required. To calculate the LCOE using the NREL sLCOE calculator we need to input the Total Capital Required. According to EPRI 2010, we need to increase TPC by 93% to get TCR.
Martin Burkle, et al,
Department of Resources Energy and Tourism (DRET) has posted an update of the EPRI figures on their web site at:
http://www.ret.gov.au/energy/facts/Pages/EnergyFacts.aspx
Points of interest:
1. The cover page here http://www.ret.gov.au/energy/Documents/facts-stats-pubs/2011/AEGTC-2011-Fact-Sheet.pdf explains how AEMO contracted ACIL-Tasman to conduct a review of the EPRI (2010) report for both AEMO and DRET. A “Stakeholder Reference Group” reviewed the EPRI data and “updated” it.
2. ACIL-Tasman did the work (they are highly competent, respected and trusted by industry. I’d trust them on this more than just about anyone else in Australia).
3. 25 technologies are listed. Nuclear is not!
4. That is, nuclear was specifically excluded from the information available to the public, despite nuclear being included in the EPRI (2010) report!
5. The data is available in Excel spreadsheets. This is the link for fossil fuels: http://www.ret.gov.au/energy/Documents/facts-stats-pubs/2011/Fossil-Fuel-Plant-Performance-and-Cost-Summary-2011.xls
6. Discount rate used is 10.1% (pre-tax real).
7. The Total Plant Cost for Black Coal without CCS ($2,408 – $2,944) is a little lower than in the EPRI (2010) report ($2,967)
8. Conversely, Total Plant Cost for Black Coal with CCS ($4,043 – $4,941) is much lower than in the EPRI report ($5,855). [I smell the hand of politics interfering here! For background, Australia is trying to lead the world to invest in an Australian led RD&D effort to solve make CCS viable. We want the world to send us lots of money for CCS RD&D.]
9. Nuclear is included in the ACIL-Tasman (2010) report
Source: Preparation of Energy Market Modelling Data for the Energy White Paper, Supply Assumptions Report. ACIL Tasman, September 2010 http://www.aemo.com.au/planning/0400-0019.pdf
10. The capital cost for nuclear (central estimate, Real 2009-10 A$/kW) = A$5,283 in 2015 and A$4,486 in 2030. (for comparison it was A$5,742/kW in EPRI (2010)). As these are 2009 A$ they would need to be reduced by about 17% to make the 2011 US$.
11. I’ll do some work on these figures and see what I come up with. I can’t see the assumptions listed for cash flow during construction, so I expect I’ll still have a problem. Interest during construction is not included in the capital cost, so it has to be calculated. The NREL simple LCOE calculator does not handle that.
12. John Newlands may want to review and comment on the projected future coal and gas prices (Section 7).
Martin Burkle, et al
I have reproduced the LCOE figures in the DRET (ACIL-Tasman) update of the EPRI (2010) report from the inputs in the Excel spreadsheet provided here. I have checked black coal without CCS and black coal with CCS (but excluding the CO2 transport and Storage line item – because I didn’t bother).
These LCOE figures do not include Owner’s Costs or AFUDC. Therefore, they are close to other commonly quoted capital cost and LCOE figures but not close to the EPRI (2010) capital cost or LCOE figures.
I have calculated an LCOE figure for nuclear based on the following assumptions which are drawn from two different reports.
Assumptions from ACIL-Tasman (2010) Excel spreadsheet:
http://www.ret.gov.au/energy/Documents/facts-stats-pubs/2011/Fossil-Fuel-Plant-Performance-and-Cost-Summary-2011.xls
Plant life (years) = 40
Discount rate (WACC) = 10.1%
Capacity Factor (%) = 85%
Assumptions from EPRI (2010) report
http://www.ret.gov.au/energy/Documents/AEGTC%202010.pdf
Thermal efficiency = 33%
Fixed O&M Cost ($/kW-y) = $146.90
Variable O&M Cost ($/MWh) = $6.10
Heat rate (kJ/kWh) = 10,900
Heat rate (Btu/kWh) = 10,331
Fuel Cost ($/GJ) = $0.94
Fuel Cost ($/MMBtu) = $0.99
My guess>
Auxiliary load = 10%
Levelized Cost of Electricity
Below I summarise the LCOE components (in $/MWh) for four analyses (columns separated by spaces):
• Coal without CCS (low value) from DRET
• Coal without CCS (high value) from DRET
• Nuclear based on the assumptions listed above
• Nuclear from the EPRI (2010) report.
Capital Charges = 33 41 81 137
Fixed O&M Cost = 4 4 20 20
Variable O&M Cost = 5 5 6 6
Fuel Cost = 7 13 10 10
LCOE = 49 63 117 173
(LCOE is real 2009-10 A$/MWh)
What I need now is:
1. the figures ACIL-Tasman would use for the O&M and fuel cost inputs
2. to understand why the EPRI report has such a high cost for what I am assuming is Owner’s Costs and AFUDC
3. to understand why ACIL Tasman is not including Owner’s costs and AFUDC in their LCOE. It should be noted that IEA, OECD, EPRI all include Owner’s Costs and AFUDC in LCOE and seem to use a figure of around 15% of TPC for Owner’s Costs. As Martin Burkle pointed out in an earlier comment, AFUDC is around 30% of TPC, but very dependent on the construction duration, the cash flow distribution over the construction period and the interest rate during construction.
That’s enough for tonight. Lot’s more to do.
Correction to previous comment,
In the comment @ 15 November 2011 at 7:30 PM, I guessed the auxilliary load as 10%. I’ve worked out that ACIL-Tasman used 8%.
That reduces the Capital component of LCOE to $79/MWh (down from $81/MWh) and reduces LCOE to $115/MWh (down for $117/MWh). This assumes that ACIL-Tasman have not changed the O&M and fuel costs for nuclear.
Since ACIL-Tasman have accepted the EPRI figure for Total Plant Cost, and since ACIL-Tasman would have no better figures to use from Australian experience than EPRI has provided, I supect ACIL-Tasman would not have changed the O&M and fuel cost inputs.
@ Peter Lang at 4.15 on 15/11 which of the reports has the price projections?
Here’s a somewhat objective basis for predictions. The Mortlake gas project in Victoria expects to pay $7/GJ. The CEO of Santos has said the price of gas will double in 20 years which is 3.5% compound. Thus if Vic piped gas is $7 in 2012 it will be ~$10 in 2022 all going smoothly.
Black thermal coal is as low as $31/t ex Cobbora NSW with the spot price ex Newcastle around $125. I’d use the same 3.5% price escalator.
What could go wrong is unexpected supply dramas. In the case of gas the Federal govt could force coal seam gas to hook up with natural gas. There could be a big shift to CNG diesel substitute if for example they dropped the diesel rebate. In the case of thermal coal maybe Mongolia won’t have as much coal as the Chinese claim and they will pay anything for Australian coal. Local generators will have to match the price when contracts are renewed.
John Newlands,
The projected fuel prices are here: http://www.aemo.com.au/planning/0400-0019.pdf
Section 7, Section 8 and Appendix A are the main sections to review.
You’ll find they not trivial. I’d be surprised if you don’t find this to be a sophisticated, analysis and projection of fuel prices.
Thank you to Scott Luft, Martin Burkle and others hwo have prompted me to look more deeply into why the large difference in the value of capital used in LCOE analysis and the difference in LCOE. I have a lot more to do on this, but just to keep you informed, here is where I am at.
I’ve sent an email off to a contact with three questions about the EPRI and ACIL Tasman reports for AEMO and DRET. The questions ask for explanation of why EPRI includes Owner’[s costs and AFUDC in LCOE analysis (as do IEA, OECD and most other’s I beleive) whereas ACIL-Tasman does not. I expect ACIL Tasman is conforming wiht a long established practice in the Australian electricity industry. However, this makes comparisons with LCOE quoted in internatioal reports difficult.
At the moment I beleive the EPRI figures are the one set of consistent figures we have. ACIL-Tasman’s (1010) are internally consistent but do not include nuclear. They exclude Owner’s Costs and AFUDC so are not ‘the full monte’.
LCOE for nuclear in 2009 A$
EPRI (2010) = $173/MWh
ACIL-Tasman (2010) = $115/MWh [Note 1]
Note 1: My calculation of LCOE for nuclear using ACIL-Tasman inputs and excluding Owner’s Costs and AFUDC as laid out @ 15 November 2011 at 9:15 PM and in the previous comment.
This highlights the very large difference in LCOE due to including or excluding Owner’s Costs and AFUDC.
By the way, on a more careful reading of the EPRI report, I now think the assumptions for calculating Owner’s costs are included; and they look reasonable to me. I’ll try to reproduce the EPRI LCOE values today.
Peter Lang I’ve looked at the AEMO planning document on coal and gas prices and so far I can’t see any statement that jars. On the general question of export parity pricing
– this is likely to apply soon to south eastern gas
– it may apply to black thermal coal as contracts expire
– it’s irrelevant to Vic brown coal.
It is possible that customers for gas and black coal ask the Federal govt to ensure that x% of production is set aside. Example if an old contract price for northern NSW black coal was $50/t but the spot price was $120. The Feds could insist that a certain tonnage of coal could not be exported so that generators had more ability to set prices.
It’s slightly weird reading these reports when they fail to mention nuclear but talk about mythological beasts like carbon capture and large scale geothermal. If there was intervention to quarantine domestic gas and coal prices from export parity critics could argue this constitutes a virtual subsidy. We see a forerunner of this in NSW
http://www.miningaustralia.com.au/news/cobbora-mine-deal-could-cost-taxpayers-6-billion
More correctly the report fails to separately discuss nuclear as it does appear in several comparison tables, never under its own heading.
JN,
Nuclear was not included in the Terms of Reference for the study. The Terms of Reference were issued by Australian Government Department of Resources, Energy and Tourism (DRET) and the Australian Energy Market Regulator (AER).
JN, I saw your comment at 7:37 am after I posted my two comments. Just to let you know, I am trying to get answers to my questions (I mentioned in a comment yesterday), but have been told “we are not in a position to answer your questions”. You can interpret what that means. I was told yesterday “Nuclear was not included in the Scope of Work”.
At the moment I am assuming, from what I’ve been told so far, the EPRI figures for nuclear have not been changed. So, whereas the cost of coal has been reduced (assumed fuel costs reduced and efficiency increased substantially), the figures for nuclear remain the same as in the EPRI report. But remember that the DRET/AEMO report does not include Owner’s Costs or AFUDC in LCOE, whereas EPRI does. Also, the Capital cost figures ($/kW) in EPRI are “net, or sent out” whereas in ACIL Tasman they are “gross”. To convert $/kW (gross) in ACIL-Tasman to $/kW (‘net’ / ‘sent out’), divide the capital cost by (1 – Auxiliary Load). ACIL Tasman gives Auxiiary Load for Super Critical Black Coal as 9.8%, and with CCS is 23.3%. I’ve calculated that ACIL Tasman used Auxiliary Load = 8% to convert the EPRI capital cost of nuclear to the capital cost in the ACIL-Tasman report.
I haven’t a clue if anyone is interested in these comments, but I am posting them to keep them all in one place and keep people up to date as to what is happening, just in case someone is interested.
Peter,
I am following everything you post. Although I am not able to contribute due to an abundance of ignorance, this thread is becoming something like a good mystery book. There’s plenty of misdirection and a slowly evolving core of probable facts. There’s a hint of political tampering. There’s a strong possibility of hidden goals. There’s even a chance to learn something new.
Keep of the good work. I hope the last chapter has a revelation that no one expected.
Peter I endorse Martin’s comments, I am continually in awe of your persistence to ferret out real data and evidence then use this information to post a comment we can all understand (usually).
Martin and Tom, Thank you. I’ll get back when I have some more information. It may take a long time to get the information I am seeking.
(The comment to which you refer has been deleted as off topic)
Peter Lang, I did notice your last post left some questions for me.
I don’t believe expanding on my previous comments would contribute to the discussion. In terms of competing interests for funds provided at cost to the government, all of the examples you give are funded directly, and often entirely, by the government where I live (health, dams, public transportation). I think that’s an unhelpful tangent.
In terms of whether the structure would be “truly a level playing field for all generators, for all energy sources,” I’m a little stumped.
My point is that the rules/playing field largely determine the successful party. I played some football/soccer decades ago, but a little game on my yard with Messi wouldn’t work out well for me.
In the winter my yard’s a skating rink. That might work for me.
I have been busy elsewhere for several days, so this evening has been catch-up time for this thread.
Gene (Comment 154, 9th November), is still having problems regarding discount rates.
Peter Lang (Comment 156) is convinced that discount rates and the LCOE are paramount.
The subsequent 60 comments have not seen any convergence of opinion, so I am returning with an example.
See: http://www.ivanhoemines.com/i/pdf/ppt/IDP_2010_PPT_May_11_2010.pdf. Ivanhoe Resources have assembled a set of 50+ Powerpoint slides to explain their commitment to a project in Mongolia costing several tens of billions of dollars. The quotation below comes from one close to the last in the set.
I provide it to introduce a concept of varying discount rates and metal prices for a copper/gold/silver mine via an analysis technique called Real Option Method. This allows analysis far more sophisticated than LCOE calculations based on starting assumptions which are then not variable.
This project indicates the strong effect that metal prices can have on the outcome. In the case of power plant, similar analysis, more detailed than we can attempt here, can and will be done by experts in respect of investments of this magnitude.
The results will quite possibly indicate similar departure from the initial assumptions, which have gold at $850/oz with a sensitivity comparison at $1200/oz. This study is only a year or two old, yet gold has since risen beyond the range, to $1900 and back to $1800/oz.
Similar price variation for fossil fuels can be expected. Gene has based his arguments on his belief that oil and gas supplies will peak and scarcity will drive higher than trended prices. There is some validity in this expectation, the problem we face is anticipating the magnitude of these swings in commodity prices. Ditto, for discount rates.
I seek to draw attention to the severe limitations of the NPV method of calculating the costs and returns of any transformative project, which in our present case includes wide application of non-traditional power generation technologies.
It is asking too much of an LCOE calculation based on a 30-line spreadsheet to expect its assumptions and outcomes to hold true beyond a few years. LCOE, in my opinion, is a tool suited to broad comparison of competing projects.
What LCOE is not suited for is:
1… It is not reliable for specific projects, for which site-specific and market-specific data must be generated.
2… It is not reliable in the presence of social upheavals such as depressions or extraordinary inflationary periods. The assumptions relating to costs of money are unreliable under such conditions.
3… LCOE cannot and does not model market behaviour in real day-to-day markets, including responses to stochiometric generation sources, to daily and seasonal peaks and lows in consumption and to variation in costs of physical inputs such as materials and labour.
4… LCOE cannot model legislative or cultural changes, as we have seen in Germany and Japan following the Fukushima earthquake and tsunami.
5…. In defence of LCOE, it is not reasonable to just ignore the value of LCOE calculations on the basis that individual observers may opine that the future circumstances are going to be different from the present. These differences must be identified and quantified. OK, they may not be able to be fed into basic LCOE models, but the example I have cited indicates that more powerful models exist.
I could go on, but readers will understand where this leads.
LCOE calculations are very much suited to comparison studies, as distinct from feasibility studies. When it comes to analysing options, especially of long-term, capital intensive projects, LCOE type studies must be supplanted by year by year financial and economic modelling to guide the decision makers. It appears that ACIL-Tasman have done so using the detail assembled in the report cited by P.L. at http://www.aemo.com.au/planning/0400-0019.pdf.
Further, the feasibility studies must be revisited every time commitment of substantial increments of capital are envisaged, eg each new power station, each new transmission line.
I caution against placing too much reliance on economic analysis, when there are other, often subjective, factors operating which are just as powerful. Examples: Perceptions of safety. Legislative and regulatory restraints. Bureaucratic inertia. NIMBY-ism. Land use planning regulations and processes. Political compromises. In some countries, corruption of officials, social and cultural considerations.
Achieving change is difficult. It is many-facetted. The speed and nature of change are not easily determined by numerical analysis, although such analysis may appear to be both compelling and persuasive. If those who are the agents of change are not listening, it matters not at all what the message may be.
Wind and solar have won the hearts and minds of the change agents and this has not been the result of LCOE or any other rational analysis: it has been entirely due to expectations of future delivery of desired results. These results may not have been delivered, but public sentiment still lies with the expensive non-performers.
Thus, it is not only or even primarily a question of cost, or of least cost. It is a question of subjective value judgement.
Nuclear power’s chance, lost sometime in the 1970′s, will not come again until the tide of public opinion demands it as strongly as the current demand for unreliables.
Gene, #170, 12 November, asks what the impediments in Oz are to NPP.
Most appear to me to be socially determined. Only after public opinion drives change will the federal and state laws which currently prevent consideration of NPP’s in Australia be repealed. Only then will safety regulation for nuclear power become based on other than “ALAP – As Low As Possible (harm)” principles, while turning a blind eye to comparatively much higher unsafety figures for competing technologies. Only after comparative measures are adopted will objectively measured environental costs of damage to the economic commons and to public health and public amenity be allocated against those industries which are cause the damage. If the governments of the world, nation by nation, cannot or will not impose appropriate pollution charges then how and when will this be addressed?
Despite perceiving these limitations to the persuasiveness of LCOE calculations, I echo Martin’s and Tom’s sentiments re the need to continue to refine our knowledge because by so doing, Peter L has unearthed a wealth of information which would otherwise have gone unnoticed.
Regarding the LCOE, there is much uncertainty in the future concerning discount rates. The current discount rates assume that the current business climate will continue and that a dollar invested will earn a certain percentage return. I do not think this is a given certainty. For example, Stansbury and Associates believes we are at the beginning of a world wide financial collapse. They have good evidence to support that belief. The US debt just passed 15 trillion dollars and is rising rapidly. Greece and Italy are at the verge of collapse which could trigger a domino effect world wide and trigger the US failing also. I am sitting here doing wind power studies and clients are slow to pay sometimes. I’m thinking that if there is a financial meltdown I may personally be in for a big loss just on outstanding invoices I currently have. This happened to me with Enron and I lost about $5000. But if we do have a world wide collapse, I’m going to have a lot more problems than just collecting. The US is so dependent on imported oil, if the dollar collapses, we are going to be out of fuel overnight for our highly dependent transportation needs. So we are sitting here argueing over whether the interest rate is 6% 8% or higher and I’m thinking that all this is irrelevant if we plunge back into the dark ages by a lack of energy in the US. Thats what worries me. Can’t you see what’s happening. Open your eyes guys and gals. We in the US are headed down a path of financial ruin and to a large degree its because we have been far too dependent on fossil fuels.
JB,
Thank you for your example of the financial analysis for a mine in Mongolia.
I’d just like to remind readers when we should use LCOE and when we should use more advanced financial analyses. LCOE is for comparison of technologies in the early screening phase, for example when a country is deciding on policy as Australia is doing now. The LCOE method is the correct method to use at this stage. It should also be noted that the sensitivity analyses can also be done, just as EPRI, ACIL-Tasman and Worley Parsons have done with the EPRI data and the updates of it.
JB, in part you are arguing that we should move the financial analysis to the next stage, sophisticated analysis for a particular site, when the screening process (including sensitivity analyses on fuel prices and a whole lot more) has shown that nuclear is not close to being viable in Australia under the current conditions (even if bans on nuclear were removed).
This is is an example of what has been called “Monkey business with numbers”.
You are also arguing that we need to change public perception. We’ve been trying to do that for 50 years. However, if it is a more expensive option (even with all positive and negative externalities included), it will not be supported. Many do not agree with your opinion about the value of the positive and negative externalities.
Instead of trying to ignore the reality – nuclear is not close to viable in Australia – we should be prepared to accept the reality and consider, with open minds, what is the cause of the problem and how could it be addressed.
I find it startling that there has been this ongoing avoidance of the real issue for two years on BNC. It seems to me the majority of contributors have preferred to try to ignore the reality rather than tackle it.
Scott Luft, @ 19 November 2011 at 10:54 PM,
I don’t understand why you say that’s an unhelpful tangent. I think it is the crux of the issue. The point is that now days, in western democracies, governments cannot raise all the money they need to pay for all the welfare state, the public services and the infrastructure that people want. Therefore, anything that can be provided by the private sector, especially if it will be managed better than by the public sector as is the case with electricity generation with appropriate (light) regulation, should be provided by the private sector. That allows the government more capacity to provide what society believes are the priorities for government to provide such as: health, education, public transport, dams, etc.
I agree the rules/playing field determine the successful party. So I don’t understand why “you are stumped”. Surely you would agree that the lower the cost of energy (with all positive and negative externalities included) the better? I presume you’d also agree that a level playing field, with all distortions removed, is the best way to achieve least cost. If you don’t accept that you must believe in the opposite; i.e. that governments, bureaucrats, environmental NGOs, the noisiest groups in society – through their demands on parliamentarians and their ability to persuade the public to accept their beliefs – can make better choices than a free market (with appropriate (light) regulation.
To help me to understand your position could you comment on what you think of this Chatham House article:
Malcolm Grimston (June 2010), Chatham House Electricity – social service or market commodity? The importance of clarity for decision making on nuclear build.
http://www.chathamhouse.org/publications/papers/view/109378
Do you think electricity should be a public service or a market commodity?
John Bennetts, @ 9 November 2011 at 12:33 PM
Are you still working on this?
I am hoping you might include a slant like: how some adaption of the Finnish TVO funding arrangements might be able to work for NSW?
My original suggestion was @ 4 November 2011 at 5:06 PM here:
http://bravenewclimate.com/2011/11/02/co2-abatement-cost-elecgen-au/#comment-140750
Five references you might find as useful starting points are included in the comment.
@John Bennets
Thank you for bringing up the Ivanhoe project in Mongolia. I have been following that quite closely, since my main interest is energy from the Gobi desert.
Actually, the Mongolian government and Ivanhoe are discussing this right now, since their first plan to pull electricity from China over a power line has hit some problems. The Chinese seem to want to use their electricity themselves.
The plans have always been to build a coal plant and this is still very likely to happen, maybe a couple of years earlier than in the original schedule.
As to cost and your point that LCOE is not everything, Ivanhoe might be interested in taking note that the World Bank just decided to give $297 million in cheap financing to Morocco for a 500 MW solar project. Anyone familiar with these questions will know that the cost of financing is not without influence on LCOE, especially with projects like nuclear and renewable where almost all of the cost is in building your plant in the first place.
The World Bank lends at LIBOR (London Interbank Offered Rate) plus 0.49%, which works out to around 1%. Good luck finding those conditions on the free market for a mining project in Mongolia. They would probably be rather less interested in financing a coal plant.
I have just written about that on my own blog as well:
http://k.lenz.de/7
Sorry, messed up the link: http://k-lenz.de/7
PL:
“Are you still working on this?”
Sorry, Peter. My presence on BNC will be curtailed for a few months due to a short term engineering engagement overseas.
JB,
Leave approved. 🙂
Peter Lang,
OK, I’ll do the reading – I’m already reading some dreary data reports related to Ontario’s ‘market’ so I’ll be some time. Your reference is a topic I find compelling.
I used to be an advocate of public power. The issues with that I’d now say are precisely the issues with everything else you noted. Collectively, I believe that Parkinson’s laws hold pretty true (‘work expands to fill the time available’). Cynically, the role of private enterprise is to make money, and the role of public enterprise is to expand the time, people, and money, required to fill the role of public enterprise. In the upcoming talks in South Africa, I’m sure they will succeed in expanding committees and planning future talks.
But, the private sector also seems more likely to compete for public contracts than to deliver a service such as electricity, and I see little value in that either. I’ve spent some time over the past few months trying to feed data, and ideas, to some economists interested in market structures required for the public interests, expressed politically, to be fulfilled by market structures. Presumably a market is to encourage competition which will serve to allocate resources efficiently. I think a regulated market likely necessitates multiple markets. Any mingling with the market is almost sure to require another supplemental market.
I’ll attempt to work-through the issues here.
Here’s a simple market roughly analogous to Ontario’s bungled attempt at a market. Providers are expected to emerge to service a market with a low:average:peak demand scenario of 1:1.5:2. In my province, we historically (with public power) decided the low (1) would be provided with low/no emission sources. That’s nuclear and hydro here, but everywhere the cleanest plants probably have high capital costs and therefore an expectation of operating at high capacity factors. I’ll assume carbon concerns are reflected in market design, so coal would be with CCS here.
Intermittent requirements are predictable, based on daily demand trends – and that’s probably some of the reason France can get the nuclear contribution so high as they manipulate output from their reactors.
So the second market is intermediate supply, and some suppliers may wish to have baseload units (running at 70% capacity -for instance), also operate in the intermediate market.
And then you’d need a market for peaking power – primarily during hot, and cold, weather. These plants only get built if they are cheap to build, or if there is another market, which would be a market bidding for capacity (availability).
Then …
we introduce either feed-in tariffs or renewable energy certificates/standards, saying 20% must come from intermittent sources. OK. Assume a 25% capacity factor on those intermittents and to get to 20% output,of the average, you’d need a total capacity 80% of the average, which is 20% more than the low demand. I think that is the real reason for nuclear being turned off in Germany! They had increasingly depressed pricing and especially worrisome, increasing periods of negative pricing due to excess supply. 1st victim = high capacity factor plants, and …
now we’d need a market for bids on removing contracted supply (baseload plus renewables), and we’d have knocked down the frequency of purchases from intermittent and peaking sources in the market.
This necessitates capacity markets – to pay suppliers to be ready. But these are the suppliers that set the price in the market, because they provide the marginal supply. The marginal supply is then offered to the market at any price over the cost of fuel (the plant is paid for through the capacity payments) – and this clean market ends up priced at the cost of gas/coal without the cost of the plant.
That is the reality in Ontario now. No new supplier will enter such a market – and the only competition is for government contracts.
Similarly, any plant that has aged to where is paid off (and this is true of many coal plants) can also offer low bids as the marginal supplier.
That says something, I think, about carbon taxes (I see your concern), but it provides me a new thought on Gene Preston’s post.
Annuities, as I understand them, are structures usually suited to an existing asset with a diminishing revenue stream. They milk an asset until it dies.
If the discount rate is based on eliminating the debt after 25-30 years, and new nuclear builds are to last 60, it seems to me in 25-30 years the nuclear plant will become, effectively, an annuity. It would not be an annuity if the company was pumping the funds back into their R&D and capital spending – but then the cost of capital wouldn’t be that high for new plant either!
I don’t recall seeing a valuation of the plant (as an annuity) after the book life period either. Over half of all generating assets, including over half of the nuclear units, in the US are over 30 years old already – http://www.eia.gov/tools/faqs/faq.cfm?id=110&t=3
I believe in functioning markets operating within the parameters of public regulation. If there is no functioning market, ownership should be public.
Scott amen to your comments! A nice writeup.
Scott Luft, on 21 November 2011 at 3:54 AM
You make some excellent points. Very clearly written. Thank you. Some I agree with and some I don’t. Although you haven’t stated it a such, I think you have, probebly unintentionally, written a comment which is an excellent explanation of why we should go the direction I’ve been advocating: remove the impediments to a freer market, reduce the regulation to only what is appropriate, remove the impediments, incentives and disencintives for any particular types of generation.
So did I.
But we are not going back to that; we are moving away from public ownership of electricity. It would take decades to move back even if the tide did change. So it is unhelpful, IMO, to advocate this because it is not a realistic option.
I suspect you are approaching this from a background and familiarity with how electricity worked under public ownership. Coming at it from that perspective you are more able to identify the problems with the (half-baked) market solution than to see the problems with trying to make the public ownership solution work since financing has changed so dramatically since the times when public ownership was the only realistic option in many western democracies.
Could I urge you to try to approach the market solution with a clean sheet of paper. Consider removing all the impediments to a true market (with appropriate, light regulation). As a first step, I hope you can read the Chatham House paper.
Below are responses to some of your comments.
That’s not a real market. It’s a pseudo-market established by bureaucrats directed by politicians who are responding to polls and media which report what the population believes is the way to go based on the noisiest and most effective scaremongering groups in society (often the Greens and the environmental NGO’s).
True for public ownership. But in a true market, competition delivers greatest efficiency and least cost (see the Chatham House paper). But we are trying to implement the middle ground which, as the Chatham House paper points out, is the worst of both options.
That is because we have a half baked solution – a pseudo-market established by bureaucrats, etc, etc.
No. The problem was caused by the intervention in the market with feed in tariffs, renewable energy targets, renewable energy certificates, direct subsidies for renewables, fast tracking of planning processes and removal of constraits for renewables but leaving them in place for other technologies, and even directly impeding nuclear as is done in many countries (even before it was banned in Germany, the German NPP’s were taxced mor heavily because they were too profitable and the extra was used to subsidiese renewables. How nuts is that. That is political interference that is almost as bad as Australia’s ban on nuclear and incentives for renewables. The answer is not more of this sort of nonsense. The answer is direct action to remove the impediments to an efficent market for energy. Light, effective regulation is needed.
Yes. We are nearly at that point in Australia too. We’ve been building a mountain of regulations on top of regulations. The whole thinng has been built by bureauctrats directed by politicians from the very start. It’s a monstrousity. Therefore, I propose we need to define the mess, then unwind much of it – as I said in previous lead articles and comments, including this comment on this thread: 5 November 2011 at 8:52 AM
http://bravenewclimate.com/2011/11/02/co2-abatement-cost-elecgen-au/#comment-140833
See pages 54 to 56 here:
http://www.chathamhouse.org/sites/default/files/public/Research/Energy,%20Environment%20and%20Development/0610pp_grimston.pdf
It begins with:
Radiation and Reason
Peter, you have been asking about what could be done to lower the cost of nuclear in Australia. I have started reading Wade Allison’s book Radiation and Reason where he suggests that “radiation is about 1000 times less hazardous than is suggested by current safety standards”. His proposal for safety levels for radiation exposure are: 100 millisievert in a single dose, 100 millisievert in total in any one month, and 5,000 millisievert total whole-of-life exposure.
It is reasonable to think that these standards would reduce the cost of plant operations, the cost on decommissioning, and the cost of disposal. These standards might affect how close plants would be built to cities or factories using the heat from a nuclear plant. However, I don’t see how these standards would affect the cost of construction. If anyone could give me a concrete (pun intended) example of cost reduction, I would be appreciative.
It would be interesting if Dr Allison’s radiation standards were adopted in Australia and combined with the idea of taking back the uranium mined in Australia to be disposed of in Australia. The moral and economic arguments could complement each other. Australia could become a supplier of all uranium life cycle processes except the reactor its self. You mine it. You enrich it. You make the fuel. You accept the used fuel. You recycle the used fuel. You dispose of the waste that is not valuable. All could be good business with great jobs. Since political policies require lots of compromise, the uranium life cycle business is just as likely as the business of building reactors in Australia.
Dr. Allison would be a good guest blogger at this site. He is a professor at the University of Oxford and teaches a course on medical physics.
Gene Preston, thank you for that.
Peter Lang, I agree with your comments. I thank you for continuing to challenge me.
I was referencing the public sector in noting the concern with ‘Parkinson’s Law”
On the problem of the introduction of feed-in tariffs, etc., I agree.
If I have any solution fighting the battle at home, I’ll be sure to communicate the successful strategy.
Scott and Peter, I think the difference between Peter and I is that Peter thinks the market can solve the utility needs and I see the market here in Texas as being an experiment that has been a flop, resulting is higher rates and very poor planning for our future needs. I have no faith the market is even capable of getting us through this rough time we are having now in Texas. And it was just a few years ago that Texas had a reliable power supply. But now now. I hope my ERCOT friends don’t see this ha ha. Oh well, doesn’t matter. By the way the local paper printed this letter today concerning the shutting down of one of our coal plants and replacing it with wind. Here is the link http://www.statesman.com/opinion/coal-power-water-conservation-1983863.html
Martin Burkle, @ 22 November 2011 at 4:21 AM
I think you have brought up what is probably one of the most important issues we need to address to reduce the cost of nuclear, especially over the longer term. A lot flows from your comment:
1. Any lifting of the overly restrictive radiation safety standards would be good. It will have more effect on the cost of future generation of reactors than on the current generation. But it should be done, and the sooner the better.
2. Any lifting of the standards reduce siting restrictions and reduce the costs of even the current generation of NPPs.
3. Any such change in the regulations could be an invaluable aid in educate the public more broadly about nuclear and its safety compared with other electricity generation technologies. For example, it would help in explaining that evacuation is not necessary, and not a rational solution, in most of the cases where leaks of radioactive materials occur.
4. However … I am a little concerned about what is the basis for the proposed new standards. My concern is: if the limits are raised to the proposed level, and they are still low compared with the other hazardous leaks we accept from other industries, then we are still locking in at too low a level. So I would like to see the new standards to be shown as comparable with the standards for the other hazardous materials that apply to other industries. I want a level playing field in terms of the health effects of radioactive contamination compared with chemical, particulate and types of contamination. However, I agree any step forward is good, so I would support what you say while arguing for a level playing field.
Scott Luft,
Thank you (and many others) for challenging me too. For me, this thread has been fascinating (as are many others on BNC). A lot of new information has come out on this thread, hopefully, we will be able to follow through further with this. I’m hoping we can continue to the next step, which in my opinion, is to work out what are the most viable ways to allow nuclear to be cost competitive in Australia (allowing for externalities where practicable and to the extent practicable given all the constraints).
I have more to do on tracking down the basis of the EPRI estimate of Owner’s Cost and AFUDC (and whatever else is burried in the figure that 93% to the Total Plant Cost to get makes Total Capital Required.
I also want to understand why ACIL-Tasman, AEMO and other Australian organisatiosn do not include Owner’s Costs and AFUDC in Total Capital Required, when it seems to be common practive to do so with IEA, OECD, EIA, EPRI to name a few.
Gene Preston, on 22 November 2011 at 7:36 AM said:
I accept what you tell us that the Texas electricity market experiment has been “a flop”. But I can only take your word for it. I expect a more correct statement may be it is not working as well as hoped. I understand similar has occurred in many other electricity markets, including in Australia.
However, I put the cause of the problem down to the fact they are not real markets. They have been established by governments and bureaucrats. Industry has had input but has not always been able to get its concerns recognised by the bureaucrats. The noisiest groups in society have been able to influence the implementation and the rules to suit what they think should be the social/green objectives. The result has been a mess in most cases. It is a case of prescription by people and noisy groups who think they know best, but don’t.
I’d also say that I doubt the Texas electricity system would be better off now had it remained in public ownership. Generally, publically owned businesses do not operate well over the long term. There are many reasons for this. But let’s not get into this discussion again. We’ve done it to death on other threads before.
Importantly, IMO, this is an irrelevant discussion, because as I’ve said repeatedly, none of the western democracies are moving back towards reintroducing public ownership. It’s simply not going to happen in our life time – unless China invades us to take the coal John Newlands wants to deny them 🙂
Did you read or re-read the Chatham House paper? What did you think of it?
http://www.chathamhouse.org/sites/default/files/public/Research/Energy,%20Environment%20and%20Development/0610pp_grimston.pdf
PL not deny coal to China just ensure the CO2 it creates is counted towards a predetermined world allowance. That is if they burn our coal to make important stuff we have to burn less.
No need for an invasion China already owns more mines than the public realises. One metal mine hereabouts I visited as a going concern is now in care and maintenance until that metal price rebounds. That’s what non-market economics can do if there is no obligatory return on capital.
JN
That is what I’ve been teilling you for yonks is what happens to mines. That is why there will be no NPP at Olympic Dam Mine nor, probably at Ceduna. The first nuclear power station in South Australia will need to be a complex of several units and located near the main demand centre, Adelaide.
By the way, what do you mean by “non-market economics”. The response to low metal prices by mothballing or shutting down a mine is pure market economics (not “non-market economics”. Mining is one of the purest markets. The price of their produces determines management decisions.
I don’t know if we discussed this or not, but the inclusion of a large amount of subsidized wind into a system causes the energy cost of other sources to increase. For example suppose we had a nearly base loaded gas plant with a capital cost component of energy cost at 1 cent per kWh. Now suppose we introduce enough wind into the system so that this gas plant generates half as much energy. Its capital cost is now 2 c/kWh. If the wind causes a 90% decrease in energy of the gas plant the capital cost of the gas plant is 10 c/kWh. The investors in the gas plant are going to become alarmed if the wind truly eats into most of the gas plant’s energy sales. The gas plant may never get built in a system with a lot of wind. Oddly the wind requires the gas plant for backup as stated in earlier postings on this blog. Yet I know of only a few instances where gas plants are combined with wind or solar. The wind developers would rather just sell the wind power and not worry about the gas plant backup. This not financing backup for wind leads to a shortage of power in the region, which is the current problem with ERCOT. I just wanted to point out that the LCOE cannot be evaluated when the energy being sold is not known in advance for a particular plant because the interaction of wind is not known in advance. Introducing wind in Australia is likely to drive up the cents per kWh energy cost of coal both through lower utilization of the coal facilities and the wear and tear on the plant itself starting and stopping to accomodate those wind generators. If Australia ever does add a lot of wind, it is likely to make the coal plants less economic and a shortage of coal capacity will result, just as in Texas. The moral of the story is that wind is not compatible with conventional generation although its needed for backup capacity.
@Peter Lang … I finished working through the Chatham House paper, and while I enjoyed it very much, I don’t think it altered my thinking.
@Gene Preston, I agree with your perspective on almost everything, but Texas is an isolated grid which, being located in the middle of a continent, really isn’t an example of open market behaviour at all (it likely does, as I suggested elsewhere, make it a good study for Australia, but it needn’t be so). I think the Texas market has acted exactly as a market would be expected to act – building marginal capacity will always be problematic, and that is exacerbated by intermittents on the grid, spurred on with, essentially, a wealth transfer scheme to get some money to the poor west Texas area.
My childhood home, in the western suburbs of Toronto, is about the same distance from Dallas as it is to the Churchill Falls reservoir in Labrador. There’s 3000MW of undeveloped hydro potential left on the Churchill/lower Churchill system, which is cited as a possibility for markets including Ontario and New England. When Texas was suffering rolling blackouts in February, and again when threatened with them in August, Ontario and Quebec had far greater than 10000MW of idle potential – if you look at the second graph on this link, of Quebec’s annual demand profile, you’ll see north North America could complement south North America quite well: http://morecoldair.blogspot.com/2011/11/reviewing-ontarios-feed-in-tariff-part.html
Peter, lets review Nordpool, the Chatham House paper’s exemplary market. Norway is blessed with abundant hydroelectric potential/capacity, and natural gas. Large hydroelectric facilities tend to be publicly owned, probably because of land-use issues. Norway is no different and Statkraft is an important player in that area. Sweden has less hydro, but still a large portion, and again publicly owned for the most part (as I understand it). Along comes Denmark (and later Germany), with big subsidies for wind and massive residential energy taxation to pay for it, and voila… you have the mix for a market.
But it is a market where the value being added is primarily to publicly owned hydroelectric generation. I think I’ve already cited, earlier on this thread, Statkraft’s terrific defense of open markets and their opposition to market-distorting capacity markets (ignoring the strategic reserve mechanism of Nordpool) In Canada I urge Hydro-Quebec to copy Norway’s policies to maximize the potential of their hydroelectric assets.
So I am not moved from my position that markets and trade are more relevant, by far, than public/private ownership. It is markets that allow for efficiency, not ownership.
Returning to the question about how to build nuclear … Ontario will soon have 2 reactors, totaling 1500MW of capacity, returning to service after over a decade mothballed, at a cost, to the private owner, of ~$4.8 million. I think the contracted cost to residents will be about 7.5 cents/kWh (Bruce reactors 1 and 2). They’ll be good for 25-30 years and then that will be the end of it. If the APRI estimates have no way of recognizing the difference in this asset, with a 30 year life, and a new asset, with a 60-year life, I suggest that is a modeling issue that isn’t accounting for future value properly.
Perhaps the way to do that is to account for the value of the asset at the end of the ‘book life’ period used in calculating the discount rate.
The UK Dept of Energy has a new version of its ’2050 calculator’ out, that for the first time attempts some costing of the user’s choices for reducing CO2 emissions.
http://2050-calculator-tool.decc.gov.uk/
The official least cost plan, which they are calling Markal 3.26, is marginally cheaper than business as usual, but that is because they are assuming $130/bbl imported oil and $110/Te imported coal, so reducing fuel use pays for the infrastructure changes.
Not much wind or solar in the least-cost mix….
Luke_UK:
Climate Spectator, yesterday, included an article under the heading “Clean energy’s Affordable Makeover”. It described a perception that public enthsiasm for renewables is giving way to a desire for affordable energy.
The 2050 Calculator Tool you brought to our attention appears to be heading further in the same direction if it indeed does reduce the emphasis on wind and solar.
My comment on the other site included:
UK Levellised Cost Study.
Digging into Luke_UK’s reference, above, I found a cost study which is very much relevant to this thread.
http://www.decc.gov.uk/assets/decc/11/meeting-energy-demand/nuclear/2153-electricity-generation-cost-model-2011.pdf
Peter Lang will find PB’s methodology and results for FOAK and NOAK across a wider range of technologies than most others.
It may provide perspective for the discussion upthread about Australian FOAK nuclear. Having only just found it, I have not digested its contents.
Thanks, Luke_UK. The site you linked to is a treasure trove. It even provides a link to the Minister’s statement which I referred to in the preceding comment.
Peter L:
Weighted Average Discounted Cost of Carbon – see P166 and thereabouts of the DECC manual at:
http://www.decc.gov.uk/assets/decc/11/tackling-climate-change/carbon-plan/3702-the-carbon-plan-delivering-our-low-carbon-future.pdf
More thanks to Luke_UK are in order. These resources appear to be quite valuable.
State of Connecticut Nuclear Analysis – 2011
“The situation might change significantly if the nuclear industry establishes good performance on the early new plant construction projects being conducted in other states and/or if significant carbon emissions penalties are implemented on generating facilities. *****Elimination of the financing premium for nuclear power plants provides a levelized cost of electricity (LCOE) that is very competitive to a CCGT power plant.*****”
In the United States we have decided that CO2 reduction is not a good enough reason to build new carbon free power generation. What we have decided is to “keep the nuclear option open”. This means that the construction of two pairs of AP1000 reactors in the SouthEast will be allowed to continue with completion dates between 2016 and 2019. If all goes well with these projects then other projects might be funded at a lower interest rates during the 2020s.
By 2020 the Chinese should have mastered AP1000 modular construction techniques by FINISHING somewhere between 14 and 24 AP1000 construction projects. I’m not sure that the Chinese think about levelized costs at all so they may not try to reduce the construction time for a single plant to 36 months. Instead they may try to optimize the construction of their fleet of reactors. It will be a fascinating/frustrating process to watch unfold in extreme slow motion.
@Peter and others: Thank you for this post and discussion. It got me interested in learning more. I wanted to get some estimates on how the system wide costs vary as we add carbon free sources into the mix. Adding wind or nuclear displaces other sources and influences capacity factors so costs elsewhere change. You can read my attempt to understand the scale of the changes: http://passiiviidentiteetti.blogspot.com/2011/12/trying-to-understand-system-wide-costs.html
Basically, I find that while the nuclear path ends up with only modest changes in the system wide LCOE all the way to the decarbonized electricity supply, the renewables path leads to escalating costs. I didn’t even postulate any particular costs reductions and used costs which appear somewhat reasonable today where I live. Of course since climbing is hard, it becomes politically harder and harder to follow to costly route as soon as the costs start to bite.
I like your approach to the issue, Jani.
EL referenced a study by Heide in the latest thread (see the Guardian questions thread comments) that looked at a 100% wind and solar Europe electricity supply. It was theoretically feasible but needed a 50% overbuild of wind and solar capacity, plus half a week of average power storage. Either of which is cost prohibitive, but especially the half a week of energy storage. The energy storage alone, even making optimistic assumptions on cost reduction of batteries, at euro 100/kWh sodium sulphur batteries, would cost 20 cents per kWh by my overly simplistic calculation. At today’s (real) cost it is 2-3x as much.
One thing that bites even harder is that if Europe needs to get more than half its electricity from wind, there won’t be enough good wind speed sites so expensive offshore and less windy (costly) onshore will have to be used. And that then needs to be overbuilt 50% (again without considering storage losses). This is already cost prohibitive even before the 20 cents per kWh half a week electricity storage system cost.
Half a week of energy storage would also add over 1 ton of batteries per capita. What is the CO2 impact of that? Lots of energy intensive chemicals such as sodium produced by electrolysis and metals produced with coal.
These cost discussions are confusing. In Jani’s link, with a number of simplifying assumptions, LCOE for hi penetration wind is about twice that of hi penetration nuclear. cyril, your numbers seem much higher.
excuse any stupidity on my part, but is that 20 cents/kwh an addition to the LCOE? That’s a huge addition, and likely underestimates according to you.
Still, someone mildly scared of nuclear might be attracted to hi penetration renewables if electricity costs “merely” doubled. I was under the impression that hi penetration renewables would be in fact cost prohibitive, but twice as much for electricity is not cost prohibitive.
I recall Peter Lang’s demonstrations involving costs far greater than double.
also: fossil fuel use seems to decline much more with hi penetration in Jani’s model than in others I have seen here. I’d really like to get clear on this.
Intuitively, I have a hard time understanding how massive overbuild would but double electricity costs. I realize there are other big issues here, like footprint, etc.
Gregory, looks like Jani actually gets very similar results. The Heide study looks at wind and solar combined in an optimal way to meet the power demand as much as the time as is possible. This should get better results than Jani, which looks at only wind.
What is interesting in the Heide study, is that it is possible to reduce the storage requirement drastically by overbuilding wind and solar. Still even with that optimization step, half a week of energy storage would be required for a completely renewable powered system for Europe.
I should note that most of Europe has very poor wind resources. Basically the vicinity of the North Sea, is excellent, much of the rest is very poor:
http://www.geni.org/globalenergy/library/renewable-energy-resources/world/europe/wind-europe/indexbig.shtml
This is a serious problem for powering most of Europe with wind. There is also NIMBY that is already very strong at today’s low European wind energy penetratioin. If one is forced towards offshore then the costs rise.
For energy storage we have to be realtic. There are not enough hydro and pumped hydro resources available so we’ll need innovative solutions such as drastically cost reduced NaS batteries and underground pumped hydro. You’ll find that there are no plausible paths for $300/kWh. Riverbank Power had a $2 billion project for 6000 MWh of underground pumped hydro storage, that’s coming in at $333/kWh. It got cancelled due to lack of suitable geology. The local residents weren’t happy about it and an activist group formed. That’s for just one project. Lots of resistance.
http://www.stopriverbank.com/news.html
Yes, its in addition to the normal cost of wind and solar. It does not include storage losses and almost neglects maintance costs. And it use favorable 5% average interest rate for the combined loan from investors and the bank. Realistically you’d be pushing 25 cents per kWh at least. If the average cost of wind and solar is 12 cents per kWh and you add 50% to that, then that makes for a busbar cost of 43 cents per kWh – no transmission and delivery costs included. Even if the average cost of wind and solar is half that (6 cents per kWh, very optimistic), the cost is still 34 cents per kWh, without transmission and delivery.
Clearly the energy storage cost is the limiting factor. So a realistic system would use less (if any) energy storage and just burn fossil fuels. And 50% overbuild isn’t interesting, so we won’t do that, either. So just burn lots more fossil fuels. And that’s the end of the transition. A mixed wind and solar and fossil grid that hasn’t gotten us the required deep (90%) reduction in fossil fuel use. We’ll have failed.
so with a 43 cents/kwh busbar, what would the real cost be, with profit added? (hope this question makes sense?)
thanks, cyril. so storage is main “limiting factor”? more than drastic overbuilding to limit storage? as you point out, of course, drastic overbuild, costs aside, runs into site/space/resistance from population issues.
thanks, cyril.
You are misreading this study. It does not call for a half a week of average power storage. 1% is an aggregate measure (when all of the charge and discharge cycles are added up over a 365 day period). There is no other way to read this in the study, or in others of the same looking at storage as an enabling technology for renewables or any other grid or generation support application: DOE, EPRI, Sandia, NREL, and various professional workshops. Let’s get this right, finally. If you think this is the contrary, please point out where this is the case.
@ EL. Storage equal to 1% of average demand means you need half a week of average energy demand flow worth of storage. This is what the Heide study says. Literally. I cannot see for the life of me how you can warp a statement as clear as this.
If, as EL suggests, the charge and discharge cycles are all added up, adding up to 1% of demand, this implies that you need only an hour or two of energy storage – when multi day low wind periods are very common. In a 100% wind and solar grid.
By deduction we can conclude this cannot be the case.
You need some more common sense to see the forest. Think about what you are saying and look at the real wind data before you claim that not much energy storage is needed in a wind and solar grid.
For refererence, here is the Heide study:
http://www.sciencedirect.com/science/article/pii/S0960148111000851
Note the word “CAPACITY”. Note also, 25% of the average annual load comes from storage (or fossil fuel, which is not acceptable of course). This is a major contributor to keep the grid together, a far cry from 1% that EL suggests.
student mode again:
there are three terms here and their relation is not clear (to moi).
long term storage energy capacity; annual balancing energy; required balancing power.
How do these terms relate to one another? what is the difference between annual balancing energy and balancing power? cyril, with your last statement about balancing power, are you suggesting that the annual balancing energy number is dubious?
Yes, energy capacity + annual balancing energy amount to 1% of the annual consumption (when all charge and discharge cycles are aggregated). I don’t know how you can have energy storage output without storage capacity? In the paper, they refer to this as “the average balancing energy.” From a direct quote: “The storage energy capacity and annual balancing energy are normalized to the average annual consumption” (p. 2517). No matter how many times you try and misread this study, it does not mean what you claim it does. 25% of the average hourly load does not mean 3.5 days of continuous replacement of energy output for an entire grid. Can we close this debate now, or risk cluttering up the thread with a lot of back and forth (when the evidence on this matter is straightforward, clear, and incontrovertible).
In Heide study, none of the annual load comes from fossil fuels … it looks at an operational model for a 100% renewables test case on a European scale (and tweaks the variables to better understand the relationship between excess generation and energy storage requirements, and generation mixes among renewables optimized for roundtrip storage, hydrogen storage, or annual balancing energy).
MODERATOR
Agreed – you should both end it here. You are never going to agree and this is becoming a circular argument.
Upon a quick review, the study I looked at, http://data.imf.au.dk/publications/thiele/2011/imf-thiele-2011-04.pdf , concludes, for storage, 16TWh of storage and 240GW of capacity. That’s highly suspect to start with, as average demand would be about 370GW, and peak I assume would be twice that.
Regardless, it then lists 105GW of salt and hydro capacity and says that’s about right(240 being right), and adds, “For one-way storage reservoirs and [renewable power at 1.5 times demand] the required annual balancing energy and power based on daily, instead of hourly power mismatches turn out to be 30TWh and 90GW, respectively.”
Well, that’s nice. Not having peak demand is, I suppose, a great way to deal with supply meeting peak demand. 90GW of storage capacity still wouldn’t be able to meet an an average demand of 370GW much of the time – but it’s less than the 105 that they found could exist …so problem solved
By the way, they do end up stating 25TWh of annual storage based on annual demand of 3240TWh – and that is about 0.8% which does equate to around 3 days. Obviously.
The problem isn’t that, in this paper, the problem they gloss over is meeting demand when demand exists to be met – which they choose not to do.
Just in case I am wrong (and some of these terms are a bit confusing in the paper), here are some relevant quotes from the conclusion. Annual European consumption in 2007 is reported as 3240 TWh in paper.
For me, the main utility of this paper (and likely the purpose intended by the author, although this is pure conjecture on my part) is to quantify the effect of excess generation and resource mix on energy storage variables. I do not think it’s a useful guide or a practical model for a fully developed technology pathway to a 100% renewable energy grid. It’s simply looking at resource mix and excess generation, and making some “hypothetical” statements on how we should look at these variables in more concrete, cost-effective, and practically oriented studies (likely looking at much smaller renewable energy targets in future cost effective and balanced energy portfolio options and mixes). In short, what types of questions should we be asking. If you think I am recommending a 100% renewables option, you would be wrong. I do not think this would be a good solution for a cost-effective or practical strategy for deep GHG reductions, or make the best use of capacity reserves or storage (which by most measures, and future expectations, will continue to have a high cost).
Thanks for direct link to article, Scott! This is what they seem to be saying, but this does not directly follow from the quote in the paper. The direct quote: “Twenty of them would provide a storage energy capacity of 25 TWh with a discharge power of 50 GW” (p. 10 above reference).
25 TWh of energy would amount to some 500 hours of continuous output at 50 GW storage capacity. How do you understand this odd discrepancy?
They appear to have very different meanings for the term “capacity” and “discharge power” in the paper.
EL, I thought you said a few comments ago you were going to close this rather than going back-and-forth?
I don’t see much practical utility in the paper (and I see you don’t either). When discussing balancing energy, it is talking about existing hydro, not hypothetical pumped hydro which would be required if the overbuilt renewable infrastructure was to dump its excess generation into — and as Peter Lang and others have shown, turning the former into the latter is a mammoth undertaking.
EL, I thought that the first figure refers to how much power needs to be stored (ie. wind generated in the spring would allow reservoirs to stay full until the summer).
I think the second number was calculated without regard for the first, which was how much energy might have to come from storage at any one time.
I don’t think the paper closes that gap – which is problematic. With the little time I have to look at it, it seems it put a little drain on a big bathtub.
[…] the movies did not import properly into wordpress. You can find the original here.)Some time ago in Brave New Climate Peter Lang wrote an interesting post on the CO2 abatement costs in Australia. He found that nuclear power is […]